0601

Statistical harmonization of multi-site diffusion tensor imaging data with ComBat
Jean-Philippe Fortin1, Drew Parker2, Birkan Tunç2, Takanori Watanabe2, Mark A. Elliott2, Kosha Ruparel3, Ruben C. Gur3, Raquel E Gur3, Robert T. Schultz4, Russell T Shinohara1, and Ragini Verma2

1Department of Biostatistics and Epidemiology, University of Pennsylvania, Philadelphia, PA, United States, 2Department of Radiology, University of Pennsylvania, Philadelphia, PA, United States, 3Department of Psychiatry, University of Pennsylvania, Perelman School of Medicine, Philadelphia, PA, United States, 4Center for Autism Research, Children's Hospital of Philadelphia, Philadelphia, PA, United States

Synopsis

Diffusion tensor imaging (DTI) is a well-established magnetic resonance imaging technique to study microstructural changes in the white matter (WM). DTI images suffer from unwanted inter-scanner variability, which is problematic when combining datasets from different sites. In this work, we propose to use ComBat, a location-scale Empirical Bayes model largely used in genomics, to combine and harmonize multi-site DTI datasets. Using a study of 210 subjects with an age range of 8 to 18 years old from two imaging sites, we show that ComBat (1) removes unwanted variation associated with imaging site and (2) improves the power at detecting regions known to exhibit microstructural changes in this age range.

Background

Diffusion tensor imaging (DTI) is a well-established magnetic resonance imaging technique for studying microstructural changes in the white matter (WM) using differential water diffusivity properties across brain tissues. Fractional anisotropy (FA) and mean diffusivity (MD) are two common scalar maps derived from DTI. DTI is highly sensitive to scanner differences, caused among others by heterogeneity in the imaging protocol, variation in the scanning parameters and different numbers of gradient sampling1,2. This is problematic when comparing and combining images from different imaging sites. With multiple NIH funded datasets, the lack of harmonization prevents researchers from investigating questions that can be only answered with large sample size. Failing to account for site-induced effects can lead to serious and spurious associations between the DTI measures and the phenotypes of interest. In this work, we adapt ComBat3, a location-scale Empirical Bayes model largely used in genomics, to combine and harmonize multi-site DTI datasets.

Methods

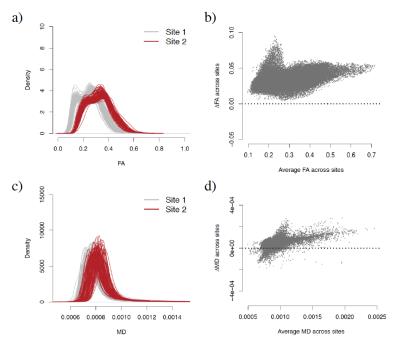
We obtained FA and MD maps from 210 subjects, acquired at two imaging sites (105 scans per site), matched for age, gender and race. We nonlinearly registered the maps to the 2mm isotropic Eve template and considered only voxels in the WM for further analysis (69,693 voxels in total). We observed that both the FA and MD measurements were substantially affected by site (Figure 1). Below, we present the harmonization model for the FA values; the same model was used for MD values. Below, we present the harmonization model for the FA values; the same model was used for MD values. Let $$$y_{ijv}$$$ be the FA value for the voxel $$$v$$$ in the j-th scan of site i. The ComBat method assumes the location and scale (L/S) model

$$ y_{ijv} = \alpha_v + X_{ij}\beta_v + \gamma_{iv} + \delta_{iv}\epsilon_{ijv}$$

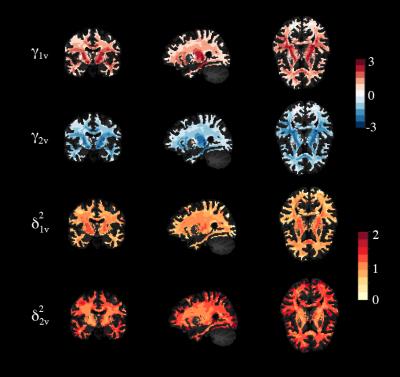
where $$$\alpha_v$$$ is the average FA measure for voxel $$$v$$$ across subjects, $$$X$$$ is the design matrix of the covariates of interest in the study (e.g. age and gender) and $$$\beta_v$$$ are the voxel-specific regression coefficients corresponding to $$$X$$$. The terms $$$\gamma_{iv}$$$ and $$$\delta^2_{iv}$$$ are the location and scale parameters for voxel $$$v$$$ that are specific to site $$$i$$$. This allows different brain regions to be differentially affected by scanner and site effects. We assume that the error terms $$$\epsilon_{ijv}$$$ are normally distributed with mean zero and variance $$$\sigma_v^2$$$. The location and scale parameters are estimated using Empirical Bayes (EB) to borrow strength across voxels to improve the statistical inference3. We present in Figure 2 the estimated coefficients $$$\hat{\gamma}_{iv}$$$ and $$$\hat{\delta}_{iv}^2$$$ for both sites. We set the site-corrected FA values to be

$$y_{ijv}^{\text{Corr}} = \frac{y_{ijv}-\hat{\gamma}_{iv}}{\hat{\delta}_{iv}}.$$

Results and Discussion

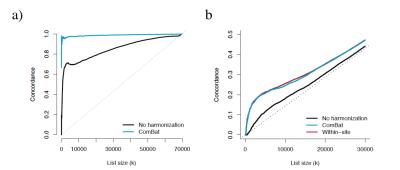
Without harmonization, 99% and 57% of the WM voxels are significantly associated with site (Bonferroni-corrected p-value < 0.05) for the FA and MD maps respectively. After ComBat, we found no voxel significantly affected by site. Furthermore, ComBat increases the power of detecting voxels associated with age for both FA and MD maps, as shown by the mass-univariate t-statistics presented in Figure 3. After ComBat, we found substantially more voxels associated with age, adjusting for multiple comparisons using Bonferroni correction (Figure 3e). We note that the top voxels associated with age for FA are mainly located in the thalamic region, in the anterior and posterior limbs of the internal capsule and in the midbrain. For the MD maps, the top voxels are mainly located in the superior corona radiata, in the superior frontal lob, in the precentral region and in the superior longitudinal fasciculus. Those regions have been reported in the literature to be associated with age for the present study age group4,5,6,7,8. Interestingly, we detect less voxels associated with age when combining the two sites without harmonization, as opposed to performing mass-univariate analyses on each site separately, despite doubling the sample size. This emphasizes the need of harmonization when pooling data from multiple sites, which is successfully achieved by ComBat. In Figure 4, we show that the voxels associated with age are more replicable with ComBat, using concordance at the top9. In addition, we show that ComBat is robust to small sample sizes.

Conclusion

With proper harmonization, combining DTI scans from multiple sites increases the statistical power of the analysis. We have shown that ComBat successfully removes acquisition-induced variation associated with site, and substantially increases the number of voxels associated with age for FA and MD maps. ComBat is a promising harmonization method, robust to small sample sizes. It does not require the scans to be acquired using similar protocols or similar number of gradient directions. The software is available in the R software via the SVA package10.

Acknowledgements

This research was supported by the National Institutes of Health (NIH) grant R01-MH092862 (PI: Ragini Verma).

References

1. Tong Zhu, Xiaoxu Liu, Michelle D Gaugh, Patrick R Connelly, Hongyan Ni, Sven Ekholm, Giovanni Schifitto, and Jianhui Zhong. Evaluation of measurement uncertainties in human diffusion tensor imaging (dti)-derived parameters and optimization of clinical dti protocols with a wild bootstrap analysis. Journal of Magnetic Resonance Imaging. 2009; 29(2):422-435.

2. Derek K Jones. The effect of gradient sampling schemes on measures derived from diffusion tensor mri: a monte carlo study. Magnetic Resonance in Medicine. 2004; 51(4):807-815.

3. W Evan Johnson, Cheng Li, and Ariel Rabinovic. Adjusting batch effects in microarray expression data using empirical bayes methods. Biostatistics. 2007; 8(1):118-127, 2007.

4. Vincent J Schmithorst, Marko Wilke, Bernard J Dardzinski, and Scott K Holland. Correlation of white matter diffusivity and anisotropy with age during childhood and adolescence: A cross-sectional diffusion-tensor mr imaging study 1. Radiology. 2002; 222(1):212-218.

5. Manzar Ashtari, Kelly L Cervellione, Khader M Hasan, Jinghui Wu, Carolyn McIlree, Hana Kester, Babak A Ardekani, David Roofeh, Philip R Szeszko, and Sanjiv Kumra. White matter development during late adolescence in healthy males: a cross-sectional diffusion tensor imaging study. Neuroimage. 2007; 35(2):50-510.

6. Sunita Bava, Rachel Thayer, Joanna Jacobus, Megan Ward, Terry L Jernigan, and Susan F Tapert. Longitudinal characterization of white matter maturation during adolescence. Brain research. 2010; 1327:38-46.

7. Antonio Giorgio, KE Watkins, Martin Chadwick, S James, Louise Winmill, Gwenaelle Douaud, Nicola De Stefano, Paul M Matthews, Steve M Smith, Heidi Johansen-Berg, et al. Longitudinal changes in grey and white matter during adolescence. Neuroimage. 2010; 49(1):94-103.

8. Christian K Tamnes, Ylva Ostby, Anders M Fjell, Lars T Westlye, Paulina Due-Tonnessen, and Kristine B Walhovd. Brain maturation in adolescence and young adulthood: regional age-related changes in cortical thickness and white matter volume and microstructure. Cerebral cortex. 2010; 20(3):534-548.

9. Rafael A Irizarry, Daniel Warren, Forrest Spencer, Irene F Kim, Shyam Biswal, Bryan C Frank, Edward Gabrielson, Joe G N Garcia, Joel Geoghegan, Gregory Germino, Constance Griffin, Sara C Hilmer, Eric Hoffman, Anne E Jedlicka, Ernest Kawasaki, Francisco Martinez-Murillo, Laura Morsberger, Hannah Lee, David Petersen, John Quackenbush, Alan Scott, Michael Wilson, Yanqin Yang, Shui Qing Ye, and Wayne Yu. Multiple-laboratory comparison of microarray platforms. Nature Methods. 2005; 2(5):345-50.

10. Jeffrey T Leek, W Evan Johnson, Hilary S Parker, Andrew E Jaffe, and John D Storey. The sva package for removing batch effects and other unwanted variation in high-throughput experiments. Bioinformatics. 2012; 28(6):882-883.

Figures

FA and MD measurements are substantially affected by site. (a) Histogram of the FA values for voxels in the WM for each subject, colored by site. (b) Mean-difference plot for the FA maps. At each voxel in the WM, the y-axis represents the average difference in FA between the two sites and the x-axis represents the average FA value across sites. A mean-difference plot centered around 0 would indicate no global site differences. Several voxels appear to be differently affected by site (upper-left points). (c-d) Same as (a-b), but for the MD maps.

Location and scale parameters estimated by ComBat for the FA maps. The first two rows show the voxel-specific location parameters estimated by Combat for Site 1 and Site 2 in the white matter (WM), and the last two rows depict the scale parameters. The ComBat model allows the additive and multiplicative site effects to vary by brain regions, and borrow information across voxels to improve the robustness of the estimates. We note that the parameters are estimated on a scale different from the original FA values for algorithmic stability. Corrected values are transformed back to the original scale.

ComBat improves statistical power at detecting voxels associated with age in FA maps. We computed voxel-wise t-statistics in WM, testing for association between FA values and age, for the two site analyzed separately and for the sites combined with and without Combat. We present the distribution of the t-statistics for (a) all voxels (c) voxels known to be associated with age and (d) voxels known to be not associated with age. (b) T-statistics in template space. (e) Number of voxels significantly associated with age after Bonferroni correction.

Replicability of the voxels associated with age. (a) Concordance at the top (CAT) plot for the voxels associated with age between the t-statistics calculated from each site (silver-standard) and the ones obtained from the combined dataset (with and without harmonization). CAT plots measure the replicability of the signal in the data; a curve closer to 1 is desirable. (b) CAT curves for subsamples of size 20 across sites (with and without harmonization, blue and black curves respectively) and within-site (red curve). ComBat does as well as the silver-standard (within-site, red curve), showing robustness to small sample size studies.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0601