0587

Multi-channel fMRI Denoising Based on Tensor Decomposition
Jun Cao1,2, Yilong Liu1,2, Mengye Lyu1,2, Grantham K. Pang2, and Ed X. Wu1,2

1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, People's Republic of China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, People's Republic of China

Synopsis

Conventional fMRI analysis applies spatial Gaussian smoothing to increase SNR, which does not fully utilize multichannel information in fMRI, and often lead to smearing of fMRI images. In this work, we proposed to denoise multichannel fMRI data based on tensor decomposition. Specifically, fMRI data are treated as a 3rd-order tensor, and Canonical Polyadic Decomposition (CPD) is used to approximate fMRI data with sum of limited number of rank-1 terms. Results show its effectiveness in denoising block-design task-related fMRI data, leading to increased temporal SNR and sensitivity of activation detection without sacrificing spatial resolution.

Introduction

MRI BOLD signal change is generally small, and often affected by thermal noise and physiological noise1. Spatial Gaussian smoothing2 has been widely adopted for fMRI denoising, but it leads to blurring edges. Multichannel MR data acquisition offers unprecedented advantages in accelerating MRI (including fMRI) acquisition with parallel imaging. On the other hand, multichannel information can also be used for denoising, which has not been well explored by fMRI community. Attempts have been made to use singular value decomposition (SVD) for data compression3 or image reconstruction in fMRI4. SVD is also feasible for fMRI denoising, fMRI data can be reshaped into a Casorati matrix, with row and column representing temporal and spatial dimensions, respectively. The fact that fMRI data comprise of a relatively small number of spatially coherent temporal processes makes fMRI data inherently low-rank4. Therefore, denoised image can be obtained using SVD and rank truncation. With multichannel acquisition, fMRI data can be reshaped into a 3rd-order tensor, with data from each channel concatenating as the third dimension. In this work, fMRI data is approximated with canonical polyadic decomposition (CPD)5 with a predetermined rank, and we enforce the constructed fMRI data tensor to be low rank.

Methods

Denoising based on tensor decomposition

The proposed method denoises multi-slice fMRI data in a slice-wise way. It consists of following steps:

(1) fMRI tensor formation: The multichannel fMRI data of each slice form a 3rd-order tensor (voxel-time-channel).

(2) Rank estimation: A tensor has rank R if it can be written as the sum of R outer products. A simple estimation of component number can be obtained by the size of core tensor by Tucker Decomposition6.

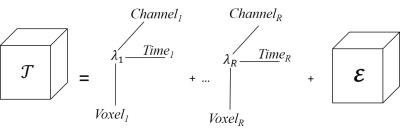
(3) Tensor approximation: 3D fMRI tensor is decomposed into R rank-1 terms using alternating least squares7 and a small residual. The sum of R terms can be considered as denoised fMRI data. Figure 1 shows pictorial representation of CPD.

$$T=∑_{r=1}^Rλ_r Voxel_r°Time_r°Channel_r+res$$

For a 3-D tensors, CPD is unique under mild conditions that

$$rank_k (Voxel)+rank_k (Time)+rank_k (Channel)≥2R+2$$

where $$$rank_k (Voxel)$$$ is Krushal rank8 of matrix Voxel.

Tensor Lab9 was used for CPD computation. As comparisons, denoising based on SVD and spatial Gaussian smoothing (FWHM=2×2×2mm3) were also implemented accordingly in the present study.

Data acquisition and analysis

Imaging was carried out on a 3T Phillips scanner with an 8-channel head coil. Functional imaging data were obtained with 2.5×2.5×5 mm3 spatial resolution and 94×94×25 spatial matrix size. 90 time frames were acquired with TR=2s. Block-design checkboard visual stimulation was used with a paradigm consisting of 3 blocks (30s ON and 30s OFF). Realignment was performed for all results in SPM. Spatial Gaussian smoothing was not performed for results with all methods. First-level GLM was used for fMRI analysis.

Results

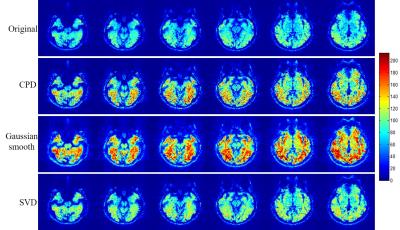
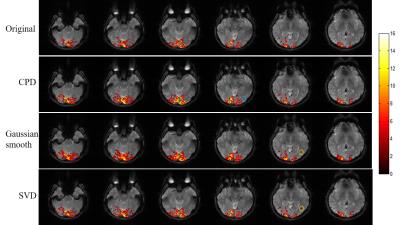
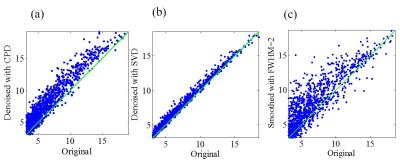
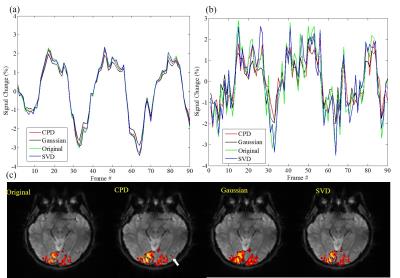
Figure 2 shows the proposed CPD and conventional Gaussian smooth methods outperformed SVD method with significantly increased temporal SNR. Figure 3 shows that with denoising, activation region expanded especially for CPD and Gaussian smooth methods. However Gaussian smooth method was observed to apparently decrease spatial resolution due to edge blurring and merging of adjacent activations. Note that some false positives were observed in Gaussian smooth and SVD results. More importantly, activation of visual area V5 (also known as middle temporal, MT)10 was detected in CPD denoising result by blue circle in Figure 3. Figure 4 shows that CPD performed the best in improving T-values. Figure 5(a) and 5(b) depicts averaged time course of all activated voxel and activated voxels within MT region (indicated in Figure 5(c)), respectively.

Discussion and conclusions

In this study, a novel method of denoising multi-channel fMRI data was proposed for improved activation mapping by canonical polyadic decomposition. fMRI data usually have a relatively small number of spatial maps associated within the data time series. The particular feature makes fMRI data low-rank inherently. CPD can be considered as a tensor low-rank approximation for original fMRI data. As demonstrated, activation maps were found to expand after the proposed CPD denoising, and T-values significantly increased. Moreover, CPD denoising method did not cause apparent false positive activation, as we have shown that true task-related BOLD signal in MT voxel was only detectable with CPD denoising method. Such increased activation detection sensitivity was the outcome of noise removal from the time course data by CPD denoising. In summary, the proposed CPD denoising method increases BOLD fMRI detection sensitivity without sacrificing spatial resolution and detection specificity. It offers the potential to substantially improve the fMRI quality, presenting an important alternative to the existing multichannel fMRI data analysis.

Acknowledgements

No acknowledgement found.

References

[1] Triantafyllou C, Hoge R.D, Krueger G, Wiggins C.J, Potthast A, Wiggins G.C, Wald L.L. Comparison of physiological noise at 1.5T, 3T and 7T and optimization of fMRI acquisition parameters. Neuroimage 2005; 26(1): 243-250.

[2] Ashburner J, Friston K.J. Voxel-based morphometry-the methods. Neuroimage 2000; 11(6): 805-821.

[3] Beckmann, Christian F, Stephen M. Smith. Probabilistic independent component analysis for functional magnetic resonance imaging. IEEE transactions on medical imaging 2004; 23(2): 137-152.

[4] Chiew M, Smith S.M, Koopmans P.J, Graedel N.N, Blumensath T, Miller K.L. k-t FASTER: Acceleration of functional MRI data acquisition using low rank constraints. Magnetic resonance in medicine 2015; 74(2): 353-364.

[5] Kolda T.G, Bader B.W. Tensor decompositions and applications. SIAM review 2009; 51(3): 455-500.

[6] Tucker L.R. Some mathematical notes on three-mode factor analysis. Psychometirka 1966; 31(3): 279-311.

[7] Cichocki A, Mandic D, De Lathauwer L, Zhou G, Zhao Q, Caiafa C, Phan H.A. Tensor decompositions for signal processing applications: from two-way to multiway component analysis. IEEE Signal Processing Magazine 2015; 32(2): 145-163.

[8] Kruskal J.B. Three-way arrays: rank and uniqueness of trilinear decompositions, with application to arithmetic complexity and statistics. Linear algebra and its applications 1977; 18(2): 95-138.

[9] Vervliet N, Debals O, Sorber L, Van Barel M, De Lathauwer L. Tensorlab 3.0, Available online, Mar. 2016. URL:http://www.tensorlab.net.

[10] Gorbet, Diana J, Frances Wilkinson, Hugh R. Wilson. An fMRI examination of the neural processing of periodic motion trajectories. Journal of vision 2012; 12(11): 5-5.

Figures

Figure 1. Pictorial representation of canonical polyadic decomposition (CPD) model. fMRI data tensor is decomposed into R rank-1 terms which contain fMRI signals and a residual term 𝓔 which contains residual noise components. The outer product of Voxelr, Timer and Channelr is the r-th rank-1 term (r=1,...,R).

Figure 2. Temporal SNR (tSNR) maps generated by different denoising methods. Both the proposed CPD method and existing Guassian smooth method outperformed SVD with significantly improved tSNR.

Figure 3. Activation maps generated by three denoising methods. Activation maps expanded using CPD and Gaussian smooth methods, while Gaussian smooth method decreased spatial resolution due to edge blurring and merging of adjacent activations. Note that both Gaussian smooth and SVD denoising methods cause some false positive activation detection as indicated in yellow circles. And activated MT voxels were detected with CPD denoising method indicated in blue circle while SVD and Gaussian smooth methods failed to detect these MT voxels.

Figure 4. Comparisons of T-values of all activated voxels; (a) CPD denoising; (b)SVD denoising; and (c) Gaussian smoothing. CPD denoising method performed the best in T-values enhancement, since SVD only improved T-values slightly and Gaussian smooth decreased T-values of many voxels.

Figure 5. (a) Comparison of the averaged time courses (extracted from all activated voxels) shows that signal changes detected by the proposed CPD were slightly higher than those by Gaussian smooth method across all blocks. (b) The time course of signal change of MT voxel as indicated by the white arrow in panel c. (c) MT activation was only detectable with CPD results. The proposed CPD method did not cause pseudo activation but smoothed the time course.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0587