0583
Blipped Stack of Spirals for Fast Volumetric Functional MRI1University of Hawaii, Honolulu, HI, United States
Synopsis
This work presents a volumetric acquisition technique for fast fMRI using spirals and parallel imaging. Gradient blips were added along the readout of a stack of spirals sequence to produce a blipped stack of spirals for a more efficient sampling scheme. Phantom images and human fMRI experiments show that the method is capable of providing approximately a factor of two speed increase compared to a standard volumetric stack of spirals.
Purpose
Spiral imaging techniques are useful for numerous fast imaging applications including fMRI (1). Typically simultaneous multi-slice or volumetric scans are also utilized in conjunction with parallel imaging and controlled aliasing to take full advantage of modern volumetric receiver arrays (2,3). Recently spiral methods were extended to a "blipped spiral" for simultaneous multi-slice fMRI with controlled aliasing (4). In this work we extend the blipped spiral technique to a Stack of Spirals (SoS) acquisition to create a Blipped-SoS sequence for fast volumetric fMRI (5). The Blipped-SoS sequence provides improved encoding along z with reduced aliasing when using parallel imaging compared to SoS. We demonstrate that the Blipped-SoS sequence can obtain approximately a speed increase of two compared to standard SoS. Both phantom imaging and human visual/motor fMRI experiments are presented.Methods
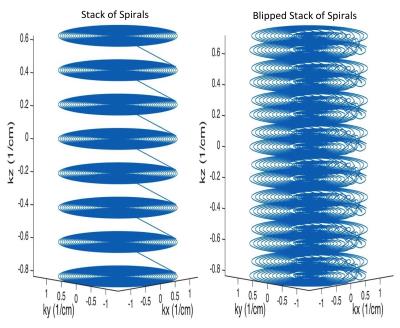
The Blipped-SoS sequence was constructed from a standard SoS sequence by introducing z-gradient blips during the spiral readout. These blips are in addition to the standard z phase encoding blips used in volumetric imaging. Figure 1 shows a diagram of the gradients as well as a blipped spiral k-space trajectory for a single z phase encoding plane. A variable density spiral was used for the x-y sampling for both trajectories. Figure 2 shows an example of an SoS as well as a Blipped-SoS volumetric k-space. It can be seen with this figure that the Blipped-SoS sequence samples k-space more uniformly than the SoS sequence.
All data were acquired using a Siemens Tim Trio 3T (Erlangen, Germany) scanner equipped with either a 4-channel or 32-channel head coil. The imaging parameters reflected what would be typical for an fMRI acquisition. Specifically, 36 3 mm slices were acquired over a 24 cm FOV with a 64x64 matrix size using a TE of 25 ms and a TR of 50 ms and a 10 degree flip angle. The z blips in the blipped spiral readout were adjusted to fill the gap along kz in the SoS k-space depending on the reduction factor Rz along z. Image reconstruction was accomplished using a generalized SENSE approach for spiral imaging (6). The k-space trajectories, sensitivity maps, and data were inserted directly into the signal equation and solved numerically using a non-uniform Fast Fourier Transform within a regularized conjugate gradient algorithm (7). All reconstructions were performed offline using Matlab (Mathworks, Natick, MA).
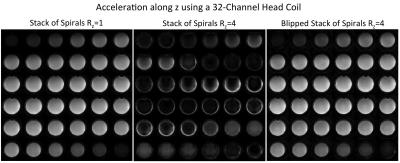
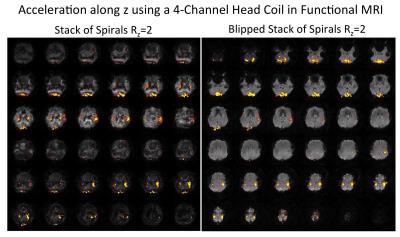
Two different imaging experiments were performed. The first was to examine the aliasing patterns in a uniform spherical phantom placed in the 32-channel coil. This coils is expected to provide some encoding power along z. Therefore a reduction factor of Rz=4 was used. The second was a human fMRI experiment using the 4-channel coil with Rz=2. The fMRI paradigm consisted of a visual checkerboard stimulation presented for periods of twenty seconds on and twenty seconds off repeated six times for four minutes. The subjects were instructed to tap their fingers during the visual stimulation to simultaneously excite both the visual and motor cortices.
Results
Figure 3 shows results from the phantom imaging experiment using the 32-channel head coil. Factors of one and four acceleration were applied along the z direction. It can be seen that the SoS sequence has severe aliasing artifacts for Rz=4 compared to the reference SoS with Rz=1. The Rz=4 Blipped-SoS acquisition however produces images that are visibly very similar to the Rz=1 reference image. Figure 4 shows human brain images with activation overlaid from the visual/motor fMRI study in an example subject. The activation was windowed to t-values between 6 to 10. These data were acquired with Rz=2 using the 4-channel coil. This coil is planar in nature and provides only minimal acceleration along z. The Blipped-SoS images produce images with much reduced aliasing compared to the SoS images. The activation patterns are also visibly consistent with those found in visual/motor fMRI studies. The SoS images however show activation aliased between the visual and motor regions.Discussion
We presented a Blipped-SoS sequence for fast volumetric fMRI with improved parallel imaging performance compared to a standard SoS sequence. The addition of the readout z blips controls the aliasing such that a more efficient usage of coil sensitivity is possible. We found that approximately a factor of two in acceleration was obtained. Further work will examine different blip schemes to create more spiral planes and interleaves as well as adding off resonance corrections and trajectory optimization. The Blipped-SoS technique will also be applied to other fast volumetric imaging applications that utilize SoS such as susceptibility weighted imaging.Acknowledgements
This project was supported by the NIH grants R01DA019912, R21EB02076, and K02DA020569.References
1. Glover, G. H. Spiral imaging in fMRI. Neuroimage 62 pp. 706–712 (2012).
2. Breuer, F. A., Blaimer, M., Heidemann, R. M., Mueller, M. F., Griswold, M. A., & Jakob, P. M. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magnetic Resonance in Medicine 53 pp. 684–691 (2005).
3. Setsompop, K., Gagoski, B. A., Polimeni, J. R., Witzel, T., Wedeen, V. J., and Wald, L. L. Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magnetic Resonance in Medicine 67 pp. 1210–1224 (2012).
4. Zahneisen, B., Poser, B.A., Ernst, T. A., Stenger, V. A. Simultaneous Multi-Slice fMRI using Spiral Trajectories. NeuroImage 92 pp. 8-18 (2014).
5. Irarrazabal, P., and Nishimura, D. G. Fast three dimensional magnetic resonance imaging. Magnetic Resonance in Medicine 33 pp. 656–662 (1995).
6. Pruessmann, K. P., Weiger, M., Börnert, P., and Boesiger, P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magnetic Resonance in Medicine 46 pp. 638–651 (2001).
7. Sutton, B. P., Noll, D. C., and Fessler, J. A. Fast, iterative image reconstruction for MRI in the presence of field inhomogeneities. IEEE Transactions in Medical Imaging 22 (2003), pp. 178–188.
Figures