Synopsis

In this abstract, variable projection sensitivity encoding (VP-SENSE) method is proposed to correct phase error, which is the main cause of Nyquist ghost in EPI. In VP-SENSE, the unknown images are fully represented by a function of phase error and the least squares solution is sought regarding phase error only. Our results have indicated that this approach can robustly remove ghost without apparent SNR penalty. With prior phase error information as constraints, ghost level can be further reduced and the SNR loss can be further minimized through constrained variable projection approach (CVP-SENSE).

Introduction

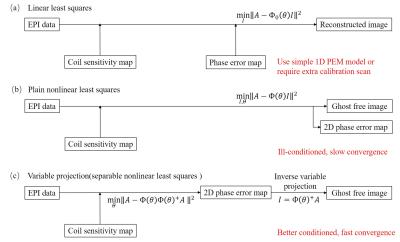
EPI is a widely used MRI application but often degraded by Nyquist ghost caused by phase error. 1D phase error model is sometimes insufficient (Fig. 1a), e.g., with oblique slice planes. 2D phase error correction usually requires time-consuming calibration scans.¹ On the other hand, it is possible to determine the 2D phase error from EPI data itself.^2,3 While direct formation of such problem regarding two variables can be ill-conditioned (Fig. 1b), we propose variable projection SENSE (VP-SENSE) as a robust calibration-free method that separately estimates phase error and images (Fig. 1c). VP-SENSE can be further enhanced by adding constrains to form constrained variable projection approach (CVP-SENESE), if an approximate 2D phase error is available.

Theory

If the positive-echo-only aliased images $$$A_p(x,y)$$$ and negative-echo-only aliased images $$$A_n(x,y)$$$ can be properly reconstructed, their corresponding aliasing-free images $$$I_p(x,y)$$$ and $$$I_n(x,y)$$$ will have the same magnitude but different phase,^4,5 i.e., $$$I_n(x,y)=e^{iθ(x,y)}I_p(x,y)$$$, where $$$e^{iθ(x,y)}$$$ is the relative phase error in negative echoes as compared with positive echoes. If multi-channel coil is used, the aliased images in each channel are $$$A_{p,i}(x,y)=S_i(x,y)I_p(x,y)$$$ and $$$A_{n,i}(x,y)=S_i(x,y)e^{iθ(x,y)}I_n(x,y)$$$, where $$$S_i$$$ is the coil sensitivity map in the $$$i^{th}$$$ coil. Without loss of generosity, let $$$I_p$$$ be the unknown images $$$I$$$ to be solved, the whole system can be described as a matrix equation, $$$A=Φ_s(θ)I$$$, where $$$A$$$ is $$$A_p$$$ and $$$A_n$$$ combined and $$$Φ_s(θ)$$$ is a general encoding function regarding phase error, given the known coil sensitivity maps. The corresponding least square solution is

$$\min \limits_{θ,I} ||A-Φ_s (θ)||^2 (Eq.[1])$$

Although both $$$I$$$ and $$$θ$$$ are unknown initially, Eq.[1] has a special structure that $$$I$$$ can be represented by $$$θ$$$ using the variable projection (VP)⁶ method, i.e., $$$I=Φ_s(θ)^+A$$$, where $$$Φ_s (θ)^+$$$is the pseudo-inverse of $$$Φ_s (θ)$$$. In summary, VP simplify the Eq. [1] to be

$$\min \limits_{θ} ||A-Φ_s (θ)Φ_s(θ)^+A||^2 (Eq.[2])$$

Eq. [2] can be efficiently solved as a pixel-wise operation. It has better conditioning and convergence property than Eq. [1]. Furthermore, it can be enhanced by constrained variable projection(CVP) method as Eq.[3], if an initial estimation of the phase error is available.

$$\min \limits_{θ} ||A-Φ_s (θ)Φ_s(θ)^+A||^2 + \lambda ||\theta -\theta_r||^2 (Eq.[3])$$

Experiments

Results

Fig. 2 shows the phantom images acquired in coronal and oblique imaging planes. Nyquist ghost residue remained clearly visible by LPC and plain nonlinear least squares (PNLS) and was much more severe in oblique images. However, Nyquist ghost was significantly suppressed in all images reconstructed by PAGE, VP-SENSE and CVP-SENSE.

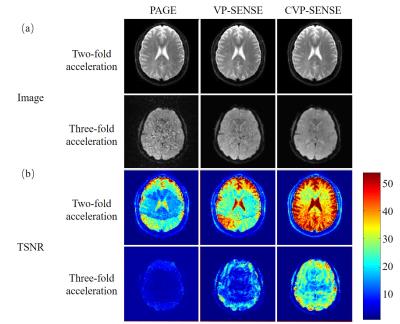
Fig. 3 shows GSRs of the four slices in Fig. 2 and SNRs of a coronal slice. The images corrected by VP-SENSE and CVP-SENSE yielded GSRs that were similar to PAGE and much better than LPC. In general, PAGE suffered from noise amplification in the aliased regions as expected. In contrast, VP-SENSE yielded lesser SNR penalty than PAGE, and CVP-SENSE could achieve almost the same SNR as LPC.

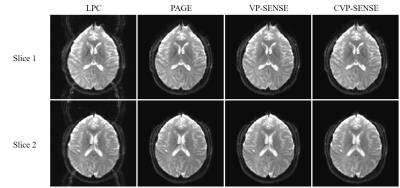
For human brain data, LPC method failed to fully remove the Nyquist ghost (Fig. 4) and the PAGE method compromised SNR (Fig. 5). Again, our proposed methods could remove the most of the ghost without sacrificing SNR.

Discussion and Conclusion

Acknowledgements

References

1. Xu D, King K F, Zur Y, et al. Robust 2D phase correction for echo planar imaging under a tight field-of-view[J]. Magnetic resonance in medicine. 2010; 64(6): 1800-1813.

2. Lee K J, Barber D C, Paley M N, et al. Image-based EPI ghost correction using an algorithm based on projection onto convex sets (POCS)[J]. Magnetic resonance in medicine. 2002; 47(4): 812-817.

3. Buonocore M H, Zhu D C. Image-based ghost correction for interleaved EPI[J]. Magnetic resonance in medicine. 2001; 45(1): 96-108.

4. Victor B. Xie, Mengye Lyu, Yilong Liu, Yanqiu Feng, and Ed X. Wu: Robust Nyquist Ghost Correction by Incorporating Phase Errors Correction in SENSE[C]. Proceedings of the 14th Annual Meeting of ISMRM. 2016

5. Chen N, Wyrwicz A M. Removal of EPI Nyquist ghost artifacts with two-dimensional phase correction[J]. Magnetic resonance in medicine. 2004; 51(6): 1247-1253.

6. Golub G, Pereyra V. Separable nonlinear least squares: the variable projection method and its applications[J]. Inverse problems. 2003; 19(2): R1.

7. Brau A C, Beatty P J, Skare S, et al. Efficient computation of autocalibrating parallel imaging reconstruction[C]. Proceedings of the 14th Annual Meeting of ISMRM. 2006; 2462.

8. Kellman P, McVeigh E R. Phased array ghost elimination[J]. NMR in Biomedicine. 2006; 19(3): 352-361.

9. Uecker M, Lai P, Murphy M J, et al. ESPIRiT—an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA[J]. Magnetic resonance in medicine. 2014; 71(3): 990-1001.