0578
Artifact Correction in Accelerated-Segmented EPI data via Dual-Polarity GRAPPAW. Scott Hoge1,2 and Jonathan R Polimeni3,4
1Radiology, Brigham and Women's Hospital, Boston, MA, United States, 2Harvard Medical School, Boston, MA, United States, 3Radiology, Massachusetts General Hospital, MA, United States, 4Harvard Medical School, MA, United States
Synopsis
A method to reconstruct images from multiple EPI segments in presented. Leveraging the reconstruction framework from Dual-Polarity GRAPPA, data from each segment and readout polarity are modeled as sampled on separate grids. After phase-matching calibration data to each segment, a GRAPPA-like reconstruction kernel is generated. This parameterization ensures that differences in signal phase across all data polarities and segments can be captured in the reconstruction kernel. We present in-vivo images reconstructed using this approach from concurrently segmented and accelerated high-resolution gradient-echo and spin-echo data acquired at 7T.
Introduction
A significant challenge in the formation of images from multi-shot segmented EPI is the proper compensation of inconsistent signal phase between the multiple segments. With multiple segments, phase errors manifest as ghosting artifacts. Phase errors arise from both scanner imperfections and dynamic physiological changes in the subject, and are often spatially non-uniform. Low-order phase correction techniques are often inappropriate and under-perform. We seek to correct inconsistent phase signal between positive (RO+) and negative readouts (RO-) based on 2D training data by applying the recent Dual-Polarity GRAPPA1 (DPG) method to segmented EPI data. We identify 2D phase differences between segments, modulate the DPG calibration data to match those phase differences, and then generate DPG reconstruction coefficients to form an image from EPI data that are both segmented and accelerated.Methods
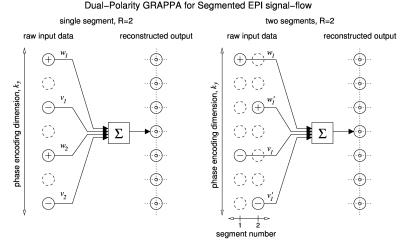
Fig. 1 illustrates the difference between DPG for single-shot and segmented EPI for the case of R=2 acceleration. At left, an example DPG kernel generates a weighted sum of 4 $$$k_y$$$ source points to generate each target point. The data samples are acquired in a single shot, and alternate between RO+ and RO- lines. In 2-shot segmented EPI (Fig. 1, right) the $$$k_y$$$ separation in each segment is increased by a factor of S=2, and lines from the two shots are interleaved to form source data with the same effective acceleration rate as the single-shot acquisition. In segmented EPI, the proposed DPG reconstruction treats the RO+/RO- data from different segments as sampled on separate grids. Whereas DPG for single-shot data employes two source data grids corresponding to the two readout gradient polarities for calibration, DPG for S-shot segmented EPI employs 2*S source data grids. This enables the parametrization provided by DPG to model and compensate for phase errors between both RO+ and RO- data and between different segments. Segmented EPI data were collected on a 7T whole-body MRI scanner (Siemens Healthineers, Erlangen, Germany) with a modified gradient-echo (GE) and a modified spin-echo (SE) sequence. GE protocol: TR=1.09 sec; TE=120 msec; SE protocol: TR=3.14 sec; TE=50 msec; 35 slices, 31 channel head coil.matrix size: 128x128; FOV 19.2 cm2; slice thickness=1.5 mm. Effective acceleration R=3; number of segments, S=2. Temporally-encoded calibration data were acquired prior to image acquisition1. From the ACS data, three images were generated: one each for data collected on RO+ and RO- gradients only, and a ghost-free target image generated from GESTE2 processing of the RO+ and RO- images. Two sets of DPG reconstruction parameters were generated from these three sets: one to reconstruct an image from a single segment, $$$G_{(S\cdot R)}$$$; and one to reconstruct an image from multiple segments, $$$G_{R}$$$. To align the phase between the segments of the DPG source data, a fully-sampled image was reconstructed from each individual segment using DPG, i.e., each segment was reconstructed using an effective under-sampling factor of $$$S\cdot R$$$. The relative phase difference was then calculated between these image estimates.DPG kernel coefficients for $$$S$$$ segments and a $$$k_y$$$ separation of $$$R$$$ were then calculated. The resulting kernel was then applied to the original $S$ segments to form the final image. For comparison, images were formed using a standard Nyquist ghost correction approach, the Local Phase Correction (LPC) method of Feiweier3. The 3-line phase correction navigator data acquired prior to the EPI echo train was used to estimate the LPC linear and constant (i.e., 1D) phase correction parameters for each segment independently. The segments were then combined and reconstructed using GRAPPA with a kernel calibrated fora $$$k_y$$$ separation of $$$R$$$.Results
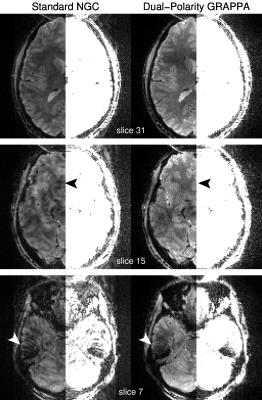
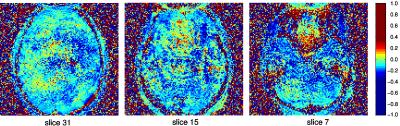
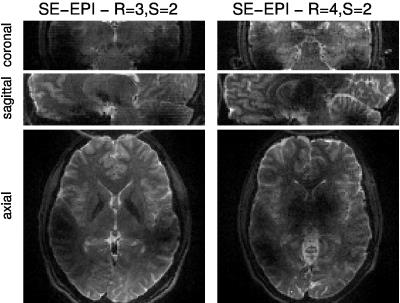
Fig. 2 shows images comparing reconstructions from the standard LPC method and the proposed DPG approach. Reconstruction artifacts are notable in the LPC images, particularly in regions near local field inhomogenieties. This is confirmed in Fig. 3, which shows the 2D phase difference between data sampled during different segments, with the strongest phase differences appearing above the nasal sinuses and the ear canals. Fig. 4 illustrates that the method is applicable to segmented spin-echo EPI, with high qualiity images shown at both R=3 and R=4 and S=2 segments.
Conclusion
We have demonstrated that our Dual-Polarity GRAPPA approach for reconstructing images from multiple EPI segments can produce images with minimal phase error artifacts. Further, the parameterization enabled by the method enables correction of 2D phase errors caused by small shifts in echo time between the segments. We anticipate this reconstruction approach will enable very high spatial-resolution protocols for fMRI, and open the possibility of MRI measurements from spin-echo EPI at echo-times that are better matched to the BOLD signal, particularly at ultra-high field strengths.Acknowledgements
Support for this work was provided in part by the Functional Neuroimaging Laboratory at the Brigham and Women's Hospital, NIH NIBIBK01-EB011498 and R01-EB019437, and by the Athinoula A.Martinos Center for Biomedical Imaging.References
1. Hoge WS, Polimeni JR. Dual-polarity GRAPPA for simultaneous reconstruction and ghost correction of EPI data. Magn Reson Med. 2016; 76(1):32-44.
2. Hoge WS, Tan H, Kraft RA. Robust EPI Nyquist ghost elimination via spatial and temporal encoding. Magn Reson Med. 2010;64(6):1781–1791.
3. Feiweier T. Magnetic resonance method and apparatus to determine phase correction parameters, 2013. US Patent 8,497,681.
Figures
Fig. 1. A comparison between standard DPG and DPG for segmented EPI, with a 4-$$$k_y$$$-point kernel. In standard DPG, the RO+ and RO- lines are interleaved. In DPG for segmented EPI, the $$$k_y$$$ distance between each sampled lines is increased by the number of segments, $$$S$$$, and the interleave groups like-polarity data. Further, the number of source data grids is increased by $$$S$$$. This enables DPG to compensate for complex phase errors between RO+ and RO- data, and across multiple segments.
Fig. 2. A comparison in images formed from {R=3,S=2} segmented data via traditional LPC ghost correction and DPG for segmented EPI. The arrows highlight regions that exhibit artifacts from inconsistent phase correction in the raw data. Notably, ripples are seen in areas above regions of magnetic susceptibility, particularly the nasal sinuses and the ear canals. Because DPG can correction compensate for phase errors in these regions, the extent of these ripples is significantly reduced in the DPG images.
Fig. 3. Normalized phase difference images generated from DPG reconstruction of the individual segments that contribute the images shown in Fig. 2. The same DPG kernel was used to construct images from bothseg1 and seg2, so the phase difference shown reflect subtle phase changes in the imaging plane between the two acquisitions. Particularly notable are the stronger phase changes that correspond to ripple regions in Fig. 2, reflecting the effect of local field inhomogeneity on the acquired signal.
Fig. 4. Images reconstructed segmented spin-echo EPI data, from two separate subjects acquired at {R=3,S=2} (left) and {R=4,S=2} (right) with a 31 channel head coil at 7T.