0577

Effect of Concomitant Field in Fast Spin Echo Acquisition on an Asymmetric MRI Gradient System
Shengzhen Tao1, Paul T Weavers1, Joshua D Trzasko1, Yunhong Shu1, Erin M Gray1, John Huston III1, and Matt A Bernstein1

1Radiology, Mayo Clinic, Rochester, MN, United States

Synopsis

Fast-spin-echo (FSE) acquisitions are routinely used in clinical MRI, but can be affected by concomitant field (CF)-induced phase errors. The conventional whole-body MR gradient typically employs symmetric design. On such systems only CFs of 2nd-order spatial dependence are significant. These CFs can cause ghosting in large-FOV FSE acquisition, but are typically negligible over a brain scan volume. Recently, a high-performance, asymmetric gradient system was developed whose CF contains additional zeroth and first-order spatially-dependent fields. Here, we investigate the effect of CF in FSE on this system using extended-phase-graphs simulation, and demonstrate a real-time compensation for them.

Purpose

Carr-Purcell-Meiboom-Gill (CPMG) condition-compliant fast (or turbo)-spin-echo (FSE) acquisitions are routinely used in clinical MRI, but can be prone to phase errors from various field perturbations including eddy current (EC) and concomitant fields (CF)1-4. The conventional whole-body gradient system typically utilizes symmetric design, and their CF contains only fields of 2nd-order or higher spatial dependence4. These CFs were shown to cause ghosting in FSE images with a large FOV, but their effect is small in FOVs used for brain scanning with the gradient specification available on most whole-body scanners3. Recently, a high-performance, asymmetric MRI gradient was developed. This system is capable of 80mT/m gradient amplitude and 700T/m/s slew rate with greatly reduced peripheral-nerve-stimulation risk due to its compact size (26-cm diameter-spherical-volume) designed for brain, infant, and extremity imaging5. The high-performance gradient can substantially shorten echo-spacing in FSE and improve imaging performance. However, due to its asymmetric design, the CFs of this system contains terms of zeroth and first-order spatial dependence, in addition to the second-order terms on symmetric whole-body gradients6. These additional CFs can cause prominent artifacts even within a standard brain scan FOV (~18-24cm). Here, we investigate the effect of CF in FSE on this system using extended-phase-graphs (EPG) simulation, and demonstrate their correction using a real-time compensation.

Methods

The signal strength of a train of echoes in a FSE sequence was simulated using EPG7-9 with acquisition parameters detailed in Table1. Only the effect of phase-encoding (PE) gradient was simulated due to its strong amplitude on our system (78.6mT/m), and the fact that the readout gradient is symmetric along refocusing pulse and is not expected to cause significant CF artifact4. A sagittal scan with PE gradient on the physical y-axis was chosen as the CF artifacts are most prominent in this configuration. Simulation was performed including all CF terms (0th, 1st, 2nd), only 1st and 2nd-order, only 0th and 2nd-order, and only 2nd-order, respectively, to separate the effects from different terms. In addition, the American College of Radiology (ACR) phantom and the brain of a healthy volunteer were scanned under an IRB-approved protocol (Table1). The real-time gradient pre-emphasis-based method10 was utilized to compensate for the first-order CF. A real-time, zeroth-order CF compensation was performed by adjusting the RF transmitter/receiver frequency according to the applied gradient waveforms, similar to real-time B0 EC correction11. These compensations were switched on and off to observe effects from different terms. The effect of an optional zeroth/linear EC correction (ECC) module (“phase correction”) available on GE’s system12 was also tested and its interaction with CFs was examined.

Results

Figure1 shows an example of echo signal strength along the echo train in a FSE acquisition obtained from simulation. The 2nd-order CF has negligible effect, while the 0th/1st-order CFs cause considerable signal loss along the echo train even at 5cm away from isocenter. Figure2 shows the pixel intensity maps across the 26cm FOV obtained from simulation after zeroth and/or first-order CF correction (CFC) (see captions). The value of each position was calculated from the peak of point-spread-functions separately computed after weighting the k-space by the echo signal strength along PE direction. The phantom images acquired with matching parameters show good correlation with simulation. The slight tilting of black band in phantom images is suspected to be due to EC effect. The black band and signal loss are largely reduced after 0th/1st-order CFC. Figure3 demonstrates the interaction between the standard, commercially-available ECC and the 0th/1st-order CFs. ECC causes image degradation if the CFC is not performed (Figure3a vs 3b). Figure4 shows in vivo examples confirming these observations (see captions).

Discussion

The zeroth and first-order CF on the asymmetric gradients can cause considerable signal loss along echo train in a FSE acquisition. These CFs manifest as local black band or global signal loss, and their effect is expected to be strong for long TE acquisition, as large phase error generated from high-amplitude PE gradients during early echoes can propagate throughout the echo train. We also note interaction between the standard ECC and 0th/1st-order CFs. This is expected as their phase accumulations can add on each other and change the appearance of artifacts.

Conclusion

We analyze the effect of the zeroth and first-order CFs from asymmetric gradients in a FSE acquisition assuming satisfied CPMG conditions, and demonstrate that their correction can improve image quality acquired on such systems. The effects of the zeroth/first-order CFs are relatively well-known for EPI and spiral acquisitions. This work demonstrates the importance of real-time, zeroth and first-order CF compensation when using asymmetric high-performance gradients even for routine anatomical imaging.

Acknowledgements

This work was supported in part by the NIH grant R01EB010065.

References

1. Hennig J, Nauerth A, Friedburg H. RARE imaging: A fast imaging method for clinical MR. Magn Reson Med 1986;3:823-833.

2. Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Burlington, MA: Elsevier Academic Press; 2004.

3. Zhou XJ, Tan SG, Bernstein MA. Artifacts induced by concomitant magnetic field in fast spin-echo imaging. Magn Reson Med 1998;40:582–591.

4. Bernstein MA, Zhou XJ, Polzin JA, King KF, Ganin A, Pelc NJ, Glover GH. Concomitant gradient terms in phase contrast MR: analysis and correction. Magn Reson Med 1998;39:300–308.

5. Lee SK, Mathieu JB, Graziani D, et al. Peripheral nerve stimulation characteristics of an asymmetric head-only gradient coil compatible with a high-channel-count receiver array. Magn Reson Med 2015; doi: 10.1002/mrm.26044.

6. Meier C, Zwanger M, Feiweier T, Porter D. Concomitant field terms for asymmetric gradient coils: consequences for diffusion, flow, and echo-planar imaging. Magn Reson Med 2008;60:128–134.

7. Hennig J. Multiecho imaging sequences with low refocusing flip angles. J Magn Reson 1988;78:397-407.

8. Hennig J. Echoes - how to generate, recognize, use or avoid them in MR-imaging sequences. Part I: Fundamental and not so fundamental properties of spin echoes. Concepts in Magnetic Resonance 1991;3:125-143.

9. Hennig J, Weigel M, Scheffler K. Calculation of flip angles for echo trains with predefined amplitudes with the extended phase graph (EPG)-algorithm: principles and applications to hyperecho and TRAPS sequences. Magn Reson Med 2004;51:68-80.

10. Tao S, Weavers PT, Trzasko JD, Shu Y, Huston J, Lee SK, Frigo LM, Bernstein MA. Gradient pre-emphasis to counteract first-order concomitant fields on asymmetric MRI gradient systems. Magn Reson Med 2016;DOI: 10.1002/mrm.26315.

11. Crozier S, Eccles CD, Beckey FA, Field J, Doddrell DM. Correction of eddy-current-induced B0 shifts by receiver reference-phase modulation. J Magn Reson 1992;97:661–665.

12. Hinks RS, inventors; General Electric Company, assignee. Fast spin echo prescan for MRI system. US patent, 5,378,985, 1995.

13. Stanisz GJ, Odrobina EE, Pun J, Escaravage M, Graham SJ, Bronskill MJ, Henkelman RM. T1, T2 Relaxation and Magnetization Transfer in Tissue at 3T. Magn Reson Med 2005;54:507-512.

Figures

Figure 1: Echo signal strength of different echoes in one TR with and without the effect of concomitant fields (CF) obtained from extended phase graph simulation (corresponding to a spatial position 5cm shifted superiorly from gradient isocenter). The 2nd-order CF, which is present on both symmetric whole-body gradients and asymmetric gradients, show very small impact on echo signal (dashed blue line vs yellow line). The 0th and 1st-order CFs, which are only present on the asymmetric gradients, cause considerable echo signal loss along the echo train (see green, purple, and red lines) , unless they are compensated as in Figs. 2-4.

Figure 2: The pixel intensity maps(left panels) across the 26-cm FOV obtained from simulation after zeroth and/or first-order CF correction, and phantom images acquired with matching acquisition parameters(right). The signal-loss across echo train caused by the first-order CF manifest as a black band(a/b). The zeroth-order CF causes a global SNR degradation(c). Correction of 0th/1st-order CFs largely reduces these artifacts(d). The ghosting at phantom superior end is suspected to be residual eddy current effects. Severe distortion is apparent here because these images were acquired far from isocenter, and gradient-nonlinearity correction was not applied to illustrate the uncorrected location of the artifact.

Figure 3: Phantom images acquired with and without 0th/1st-order CF correction and the product eddy current (EC) correction (“phase correction” on GE’s system) showing their interaction. Note that the EC correction can degrade image quality with the absence of the zeroth/first-order CF correction (a vs b). The signal loss (red arrows) can be further reduced after the EC correction if the CF correction was also applied (c vs d). The ghosting close to phantom superior end is suspected to be residual eddy current effects.

Figure 4: Examples of FSE images acquired on a healthy volunteer. Note the black band caused by the first-order concomitant field (red arrows). These effects are largely removed after CF compensation (c). The EC correction applied after CF correction can further suppress ghosting observed at the peripheral of FOV (green arrows).

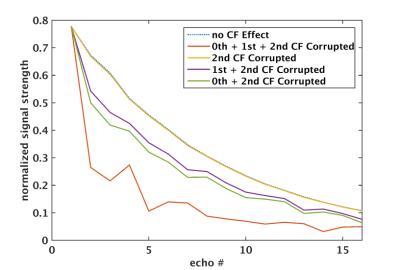
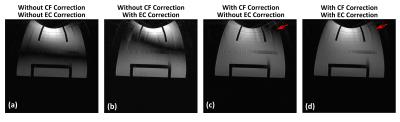
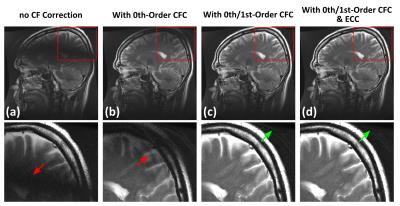
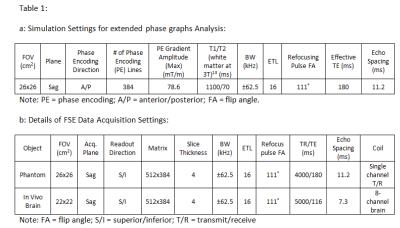
Table 1a: Simulation settings for extended phase graphs analysis.

1b: Details of FSE data acquisition settings.


Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0577