0576

Estimating and eliminating excitation errors in bipolar gradient composite excitations caused by RF-gradient delay: example of bipolar spokes pulses in parallel transmission

Desmond H Y Tse¹, Christopher J Wiggins², and Benedikt A Poser¹

¹Faculty of Psychology and Neuroscience, Maastricht University, Maastricht, Netherlands, ²Scannexus BV, Maastricht, Netherlands

Synopsis

Parallel transmission of spokes pulses is a promising way of mitigating flip-angle inhomogeneity in 2D imaging at ultra-high-field MRI. Bipolar slice-selective gradient is often used to minimise the overall duration of these pulses, making them more resilient to off-resonance related artefacts, but they are prone to errors caused by RF-gradient timing mismatch. In this study, we present a mathematical description for the effect of such delay on bipolar-gradient composite excitations. We demonstrate the effect with both flip-angle maps and EPI images. Finally, we propose a navigator approach to estimate the delay and show two effective ways of eliminating these errors.

Purpose

To eliminate a slice-position dependent excitation error commonly observed in bipolar-gradient composite excitations such as spokes pulses^1-4 in parallel transmission.

Theory and Methods

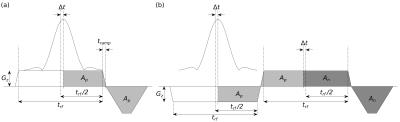
A time delay of $$$\Delta{t}$$$ between a symmetric RF pulse and its slice-selective gradient^5-12 (Fig. 1) gives rise to a phase difference $$$\Delta\phi$$$ between the odd and even sub-pulses in a bipolar composite excitation: $$\Delta\phi=2\gamma{G_{z}}\Delta{t}z=4\pi{BW}\Delta{t}\frac{z}{\Delta{z}},(1)$$ where $$$\gamma$$$ is the gyromagnetic ratio, $$${G_{z}}$$$ is the slice-selective gradient amplitude, $$$z$$$ is the distance of the slice from the isocentre, $$$BW$$$ is the bandwidth of the RF pulse and $$$\Delta{z}$$$ is the slice thickness. The actual achieved excitation pattern (effective flip-angle) will deviate from the expectation when $$$\Delta\phi$$$ is not accounted for during the pulse design.

We propose a dual-echo navigator as shown in Fig. 2 to measure the delay, and subsequently eliminate the error. This is demonstrated with in vivo experiments on a 7 T whole-body MR scanner (MAGNETOM, Siemens Healthineers, Erlangen, Germany) with a 8Ch-pTX/32Ch-Rx coil (Nova Medical, Wilmington, MA, USA). Data were acquired using SMS-pTX EPI^4,13, and flip-angle maps were measured by PreSat-TFL¹⁴. 2-spoke pulses (flip-angle=45˚, $$$\Delta{z}$$$=3.0 mm, BWTP=4.0, $$${G_{z}}$$$=32.62 mT/m, sub-pulse spacing=1.36 ms, sub-pulse duration=0.96 ms) were calculated in a slice-by-slice fashion⁴, using B₀ maps obtained by dual-echo 3D GRE¹⁵ and B₁⁺ sensitivity maps collected by a transmit phase-encoded^15,16, T₂ and T₂^* compensated version of DREAM¹⁷. Two different correction methods are demonstrated here: 1) by removing the time delay directly; 2) or by applying the corresponding slice-position dependent phase differences (Eq. 1) to the sub-pulses. In each case the flip-angle homogeneity [normalised root-mean-square error (NRMSE)] is evaluated and compared with the prediction as well as mono-polar (fly-back) excitations which served as reference.

Results

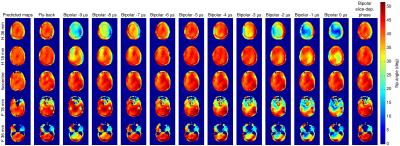
Near-perfect agreement between the observed flip-angles and predictions is achieved with both correction approaches. Fig. 3 shows the flip-angle maps of 2-spoke pulses at five different slice positions. Fly-back spokes (NRMSE=0.096), bipolar spokes with -6 μs correction of the RF-gradient starting time (NRMSE=0.093) and with slice-dependent RF phase correction according Eq. 1 (NRMSE=0.091) all agree well with each other and the pulse optimisation’s prediction.

Fig. 4 shows the excitation errors as a function of the imposed relative RF-gradient starting time in the bipolar excitations where the slice-position dependent phase is clearly seen. Good agreement is seen between the predicted NRMSE (circle), the measured NRMSE of the fly-back spokes, and both the delay-corrected and slice-phase corrected bipolar spokes.

The proposed navigator (Fig. 2d) measured a time delay of 12.6 µs between the echoes, corresponding to a $$$\Delta{t}$$$ value of 6.3 μs, which agreed well with the estimate from the flip-angle maps.

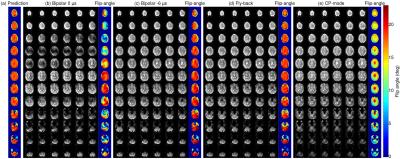
Fig. 5 demonstrates the application of 2-spoke multi-band pulses in a SMS-EPI sequence with slice-acceleration factor 2. Application of the timing correction resulted in accurately excited EPI images with bipolar dual-spokes SMS-2 excitations.

In comparison with the fly-back spokes, the shorter duration of the bipolar spokes results in increased robustness against signal intensity drop in regions where B₀ inhomogeneity is known to be severe, e.g. above the frontal sinus and the ear canals. The lower signal intensity and lower flip-angle seen in the CP-mode excitation (Fig. 5e) in the temporal lobes and the cerebellum confirm the expected benefits of flip-angle homogenisation with spokes excitations.

Discussion

We provided a mathematical description of the slice-position dependent excitation errors that occur when there is an undesired delay between a bipolar gradient trajectory and the RF sub-pulses. We furthermore proposed a navigator acquisition which can be used to rapidly estimate the timing mismatch for any desired set of excitation parameters, e.g. slice thickness, orientation and RF bandwidth. The estimated RF-gradient delay was successfully applied back to the bipolar spokes pulses in our modified sequences. The navigator described here takes less than one second to run and it can be run as a pre-scan and the timing correction applied directly to the following scans. Flip-angle maps obtained with PreSat-TFL demonstrate the efficacy of correcting the RF-gradient delay, showing that the intended flip-angle homogeneity can be restored and brought to good agreement with the predicted excitation maps. This translates into improved image quality with bipolar excitations at any off-centre slice position, as shown here by in vivo SMS-EPI acquisitions with bipolar 2-spoke SMS-pTX excitations at SMS factor 2. In general, bipolar trajectories are preferred over fly-back schemes because of their greater time efficiency which reduces excitation pulse duration, alleviates echo time constraints¹⁸ and improves spectral resolution¹⁹.

Conclusion

An effective correction is proposed to mitigate slice-position dependent errors in bipolar composite excitations with undesired RF-gradient timing delays.

Acknowledgements

We thank Dr Martijn Cloos and Dr Vincent Gras for the valuable discussions on this topic. Scan time was supported under Scannexus/Brains Unlimited development project dev_b0_b1 and intramural MBIC funding (project F8015).

References

1. Setsompop K, Alagappan V, Gagoski B, Witzel T, Polimeni J, Potthast A, Hebrank F, Fontius U, Schmitt F, Wald LL, Adalsteinsson E (2008) Slice-selective RF pulses for in vivo B1+ inhomogeneity mitigation at 7 tesla using parallel RF excitation with a 16-element coil. Magn Reson Med 60 (6):1422-1432

2. Schmitter S, Wu X, Auerbach EJ, Adriany G, Pfeuffer J, Hamm M, Ugurbil K, van de Moortele PF (2014) Seven-tesla time-of-flight angiography using a 16-channel parallel transmit system with power-constrained 3-dimensional spoke radiofrequency pulse design. Invest Radiol 49 (5):314-325

3. Wu X, Adriany G, Ugurbil K, Van de Moortele PF (2013) Correcting for strong eddy current induced B0 modulation enables two-spoke RF pulse design with parallel transmission: demonstration at 9.4T in the human brain. PLoS One 8 (10):e78078

4. Tse DHY, Wiggins CJ, Poser BA (2016) High-resolution gradient-recalled echo imaging at 9.4T using 16-channel parallel transmit simultaneous multislice spokes excitations with slice-by-slice flip angle homogenization. Magn Reson Med 10.1002/mrm.26501

5. Jankiewicz M, Zeng H, Moore JE, Anderson AW, Avison MJ, Welch EB, Gore JC (2010) Practical considerations for the design of sparse-spokes pulses. J Magn Reson 203 (2):294-304

6. Schmitter S, DelaBarre L, Wu X, Greiser A, Wang D, Auerbach EJ, Vaughan JT, Ugurbil K, Van de Moortele PF (2013) Cardiac imaging at 7 Tesla: Single- and two-spoke radiofrequency pulse design with 16-channel parallel excitation. Magn Reson Med 70 (5):1210-1219

7. Zelinski AC, Wald LL, Setsompop K, Goyal VK, Adalsteinsson E (2008) Sparsity-enforced slice-selective MRI RF excitation pulse design. IEEE Trans Med Imaging 27 (9):1213-1229

8. Davies NP, Jezzard P (2005) Calibration of gradient propagation delays for accurate two-dimensional radiofrequency pulses. Magn Reson Med 53 (1):231-236

9. Grissom W, Yip C-y, Zhang Z, Stenger VA, Fessler JA, Noll DC (2006) Spatial domain method for the design of RF pulses in multicoil parallel excitation. Magn Reson Med 56 (3):620-629

10. Wu X, Vaughan JT, Ugurbil K, Van de Moortele PF (2010) Parallel excitation in the human brain at 9.4 T counteracting k-space errors with RF pulse design. Magn Reson Med 63 (2):524-529

11. Duyn JH, Yang Y, Frank JA, van der Veen JW (1998) Simple correction method for k-space trajectory deviations in MRI. J Magn Reson 132 (1):150-153

12. Takahashi A, Peters T (1995) Compensation of multi-dimensional selective excitation pulses using measured k-space trajectories. Magn Reson Med 34 (3):446-456

13. Poser BA, Anderson RJ, Guerin B, Setsompop K, Deng W, Mareyam A, Serano P, Wald LL, Stenger VA (2014) Simultaneous multislice excitation by parallel transmission. Magn Reson Med 71 (4):1416-1427

14. Chung S, Kim D, Breton E, Axel L (2010) Rapid B1+ mapping using a preconditioning RF pulse with TurboFLASH readout. Magn Reson Med 64 (2):439-446

15. Tse DHY, Wiggins CJ, Ivanov D, Brenner D, Hoffmann J, Mirkes C, Shajan G, Scheffler K, Uludag K, Poser BA (2016) Volumetric imaging with homogenised excitation and static field at 9.4 T. Magn Reson Mater Phy 29 (3):333-345

16. Tse DHY, Poole MS, Magill AW, Felder J, Brenner D, Jon Shah N (2014) Encoding methods for B1(+) mapping in parallel transmit systems at ultra high field. J Magn Reson 245:125-132

17. Nehrke K, Versluis MJ, Webb A, Bornert P (2014) Volumetric B1 (+) mapping of the brain at 7T using DREAM. Magn Reson Med 71 (1):246-256

18. Rieseberg S, Frahm J, Finsterbusch J (2002) Two-dimensional spatially-selective RF excitation pulses in echo-planar imaging. Magn Reson Med 47 (6):1186-1193

19. Yang C, Deng W, Alagappan V, Wald LL, Stenger VA (2010) Four-dimensional spectral-spatial RF pulses for simultaneous correction of B1+ inhomogeneity and susceptibility artifacts in T2*-weighted MRI. Magn Reson Med 64 (1):1-8

Figures

Fig. 1: Schematic of a bipolar spokes excitation pulse together with their slice-selective and rephasing gradient lobes. (a) the case of the odd sub-pulses in which the slice-selective gradient has the opposite polarity to the rephasing lobe; (b) the case of the even sub-pulses in which the slice-selective gradient and the rephasing lobe have the same polarity. They demonstrate how a delay Δt between the symmetric sinc pulse and its slice-selective gradient results in different required rephasing gradient moment. This leads to a slice-dependent phase difference between the (a) positive and (b) negative lobes spokes sub-pulses given by Eq. 1.

Fig. 2: Schematic of a two-step dual-echo navigator to measure Δt. (a) First step: only the last sub-pulse (solid line) is played out. (b) Second step: only the second to last sub-pulse is played out. (c) With the sign of the time delay shown in (a) and (b), the dotted line in (c) represents the echo from the pulse played out in (a) with a positive slice-selective gradient lobe; and the solid line represents the echo in (b). (d) Navigator echoes from sub-pulses of both gradient polarities, measured with the proposed navigator approach for direct measurement of the excitation waveforms.

Fig. 3: Flip-angle maps of 2-spoke pulses measured by PreSat-TFL. The left column is the predicted flip-angle distribution from the pulse optimisation. The 2^nd column from the left shows the flip-angle maps from the fly-back spokes pulses. The next 10 columns are the flip-angle maps from the bipolar spokes pulses with the relative starting time between the sub-pulses and the slice-selective gradient set from -9 μs to 0 μs (left to right). The last column plots flip-angle maps from the bipolar spokes pulses with the slice-position dependent phases corrected using Eq. 1 and without any timing correction.

Fig. 4: NRMSE from the pulse optimisation and estimated from the PreSat-TFL measured flip-angle maps of the spokes pulses in the three configurations tested (fly-back, bipolar with relative starting time adjusted and bipolar with the slice-position dependent phase shift corrected): (a) slice at the isocentre; (b) slice at 36 mm from the isocentre; (c) slice at 54 mm from the isocentre; (d) averaged over all slices.

Fig. 5: SMS-spokes-EPI images with their corresponding excitation flip-angle maps. 2-spoke pulses were designed in a slab-specific fashion for 12 slabs. 6 neighbouring slices in the EPI protocol were grouped into one slab to share the same spokes pulse. (a) flip-angle maps predicted from the 2-spoke optimisation; (b) SMS-2 bipolar 2-spoke EPI without any correction to the relative starting time between RF and slice-selective gradient. (c) SMS-2 bipolar 2-spoke EPI with -6 μs correction to the relative starting time between RF and slice-selective gradient. (d) SMS-2 fly-back gradient 2-spoke EPI. (e) SMS-2 EPI in CP-mode.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0576