0573
Correction of Susceptibility-Related Image Distortion Based on an Analytic Point-Spread FunctionFranz Patzig1, Toralf Mildner1, and Harald Möller1
1Max Planck Institute for Human Cognitive and Brain Sciences, Leipzig, Germany
Synopsis
Geometric distortions caused by magnetic susceptibility variations in the underlying medium can severely corrupt the image. A novel correction method is proposed, which uses the prior knowledge of the analytic point spread function (PSF) of the used imaging sequence and a map of the underlying field inhomogeneities. From this input, a PSF operator can be devised and applied to correct the image by performing a deconvolution. Regularization techniques are used to improve and stabilize the outcome. A significant reduction in geometric distortions is demonstrated for human brain images as well as some advantages over existing correction methods.
Purpose
Single-shot acquisition techniques like EPI are the workhorse for functional and diffusion MRI. Due to their long read-out trains and concomitantly low bandwidth in phase-encoding (PE) direction, they are particularly prone to artifacts caused by magnetic susceptibility variations in the object introducing additional phase offsets. This problem becomes more severe at high magnetic fields. Correction methods often require additional acquisitions, such as a map of the underlying field inhomogeneities that is used in the multi-frequency reconstruction (MFR) approach [1,2] or the experimental point-spread function (PSF) in each voxel used in a PSF correction approach [3]. While the latter technique is expected to produce better outcomes, it is also more time consuming. Here, we present a technique combining a field inhomogeneity map with an analytic PSF to correct EPI images by a deconvolution technique.Methods
Analytic complex PSFs were obtained for single-shot GE-EPI and a recently suggested double-shot modification with center-out trajectories (DEPICTING [4]) by applying the inverse Fourier transform to the modulation transfer functions in k-space. The PSFs are deduced with a simplified model considering $$$T ^*_2$$$ relaxation, main magnetic field inhomogeneities, $$$\Delta B_0$$$, and truncation of k-space by the acquisition window. They were validated by experiments with water phantom scans and by simulations (Figure 1). All acquisitions including EPI and DEPICTING scans in human volunteers as well as a multi-echo-FLASH based field-map scan were performed at 3T (Verio, Siemens, Erlangen, Germany). Any measured image is a convolution of the spatially varying PSF and the underlying object, namely $$$\mbox{IMG} = \mbox{PSF} \ast \mbox{OBJ}$$$. Using an acquired $$$\Delta B_0$$$ map and the analytic PSF of the particular sequence as input, the PSF operator can be modeled and a deconvolution in image space with the discrete PSF operator yields a representation of the object that is distortion- and intensity-corrected. Only effects along PE direction are considered as they are known to dominate [5]. The deconvolution is performed by inverting a PSF matrix for every column of the image. This is an ill-posed problem and requires further regularizations, which is based on singular value decomposition (SVD). Briefly, the least-squares solution of a system of linear equations is obtained by the Moore-Penrose pseudoinverse, which can be computed inverting the SVD matrices. The inversion of low singular values was regularized as this is an unbounded operation. Furthermore, in regions of low signal intensity the field map was interpolated employing discrete cosine transforms (see figure 2).Results
Figure 3 shows an uncorrected EPI image (A), and EPI images corrected by both the MFR method (B) and the analytic PSF approach (C). In general, both methods are capable of correcting the major distortion artifacts. The PSF-based correction technique, however, additionally achieves a restoration of the signal intensity distribution and has the potential to reproduce brain structures more clearly by an inherent consideration of $$$T ^*_2$$$ blurring. This is further illustrated in Figure 4, which shows results for the DEPICTING sequence [4], where off-resonance effects are known to cause simultaneous shifts in opposite directions due to the double-shot acquisition with opposite phase blips. Figure 5 demonstrates the effect of applying the regularization strategies necessary for the PSF deconvolution. While the corrected image is highly corrupted if only the inverse of the PSF matrices is used (Fig. 5B), the quality is substantially improved employing the SVD regularization (Fig. 5C) and even more after interpolating the field map (Fig. 5D).Discussion
A distortion correction of EPI-based images was proven to be feasible by the knowledge of an analytical solution of the imaging PSF, a preparation scan ($$$\Delta B_0$$$/$$$T^*_2$$$ map) as input, and successive PSF deconvolution. The method yielded improved results when compared to the MFR method (Figures 3 and 4). In addition, computation times are reduced for the PSF-based technique. The quality of the obtained corrections also substantiates that our analytic model of the PSF approximates the real PSFs quite well and considers the relevant contributions. However, in order to stabilize the deconvolution procedure towards a meaningful result, a regularization strategy was required (Figure 5). As in the MFR approach, the quality of the proposed PSF deconvolution depends on the quality of the underlying field maps, that is, deviations between the $$$\Delta B_0$$$ distributions used for the correction and that present during EPI need to be minimized.Conclusion
A novel method for EPI image distortion correction based on analytic PSFs was introduced. Compared to the MFR technique, an improved image contrast with an inherent intensity correction was achieved. The method might be an alternative to the direct voxel-by-voxel estimation of the PSF [3].Acknowledgements
No acknowledgement found.References
[1] D.C. Noll et al., A Homogeneity Correction Method for Magnetic Resonance Imaging with Time-Varying Gradients. IEEE Trans. Med. Imaging 10: 629-637, 1991. [2] L.C. Man et al., Multifrequency Interpolation for Fast Off-resonance Correction. Magn. Reson. Med. 37: 785-792, 1997. [3] H. Zeng, R.T. Constable. Image Distortion Correction in EPI: Comparison of Field Mapping With Point Spread Function Mapping. Mag. Reson. Med. 48: 137-146, 2002. [4] S. Hetzer, T. Mildner, H.E. Möller. A Modified EPI Sequence for High-Resolution Imaging at Ultra-Short Echo Time. Mag. Reson. Med. 65: 165-175, 2011. [5] P. Jezzard, R.S. Balaban. Correction for Geometric Distortions in Echo Planar Images from B0 Field Variations. Mag. Reson. Med. 34: 65-73, 1995.Figures
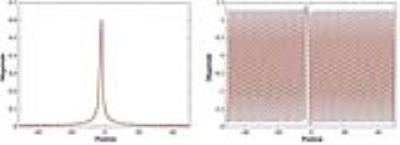
Example of
GE EPI PSF with $$$T
^*_2 = 100$$$ ms, $$$\Delta \omega_0 = 40$$$ Hz. A shift apart from the center due to
field inhomogeneities is visible. Red: simulated PSF; Blue dashed:
analytic PSF.
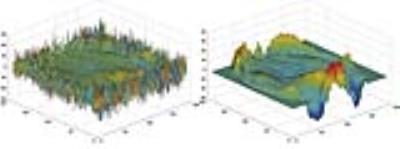
Adjustment of the used field map: Left acquired
field map from fitting 16 echoes. Right: Regularized and interpolated field
map.
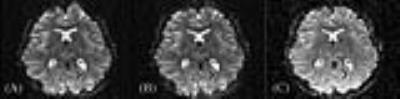
Correction of GE EPI image ($$$T_E = 70$$$ ms, $$$T_R = 4$$$ s,
FOV = 192 mm, 1.5 x 1.5 x 2.5 $$$\mbox{mm}^3$$$). (A) - Raw data from scanner; (B) - Image
corrected with MFR method; (C) - Image corrected with PSF method.
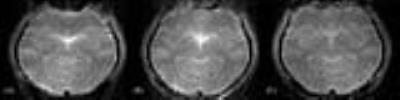
Correction of DEPICTING image ($$$T_E = 3$$$ ms; $$$T_R = 5$$$ s;
FOV = 192 mm; 1.0 x 1.0 x 2.0 $$$\mbox{mm}^3$$$). (A) - Recorded raw data; (B) - Image
corrected with MFR method; (C) - Image corrected with PSF method. An intensity
correction in the PSF corrected image is visible in the centre part.
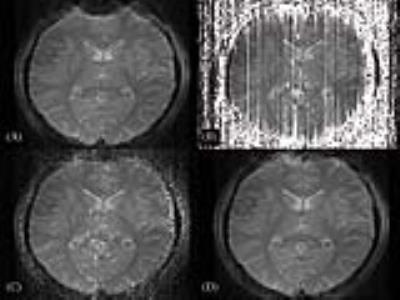
Demonstration of regularization techniques (same
scan as shown in figure 4): (A) - Uncorrected image; (B) - No regularization;
(C) - SVD regularization; (D) - SVD and field map regularization. The used
regularization techniques improve the outcome and yield a meaningful solution.