0571
Parameter-Free Profile Encoding Reconstruction for Multiple-Acquisition bSSFP Imaging1Electrical and Electronics Engineering, Bilkent University, Ankara, Turkey, 2National Magnetic Resonance Research Center (UMRAM), Bilkent University, Ankara, Turkey, 3Graduate School of Engineering and Science, Bilkent University, Neuroscience Program, Ankara, Turkey
Synopsis
Several recent studies suggested accelerating multiple-acquisition balanced steady-state free precession acquisitions to suppress banding artifacts while maintaining scan efficiency. However, these approaches employ regularization terms, which require labor-intensive manual tuning of penalty weights. Here, we propose a parameter-free framework to select penalty weights adaptively for profile-encoding reconstructions. Results indicate the proposed method achieves equivalent image quality to conventional reconstructions, without an exhaustive manual tuning of penalty weights.
Introduction
Balanced steady-state free precession (bSSFP) sequences suffer from banding artifacts near certain off-resonance frequencies1. To suppress banding artifacts while maintaining scan efficiency, several recent studies suggested accelerating multiple-acquisition bSSFP1. In an earlier study, the acquisitions were randomly undersampled and then reconstructed individually using compressed sensing (CS)2. More recently, a profile-encoding reconstruction was proposed to synthesize unacquired data linearly from k-space samples across acquisitions. In both studies, unacquired data were recovered using regularized reconstructions that employ $$$\ell_1$$$-norm and total-variation penalties weighted against a data-consistency term. While regularization significantly improves image quality, these previous reconstructions require labor-intensive manual tuning of penalty weights, often confirmed via visual inspection2,3.
Here, we propose a parameter-free self-tuning approach (SPE) to select the penalty weights in profile-encoding reconstructions. This framework adaptively alters the penalty weights during the course of iterative reconstruction, automatically optimizing the weights for each coil and each acquisition. Phantom and in vivo results demonstrate that the proposed method reconstructs images of equivalent quality to reference images that are obtained by an exhaustive brute-force search across a broad range of penalty weights.
Methods
In multiple-acquisition bSSFP, a total of N images with different RF phase increments are acquired2,3,4. To maintain a fixed total scan time, here each acquisition was accelerated by an undersampling factor of R=N. Undersampling in k-space was achieved by variable-density random sampling patterns3. Unacquired data were recovered by solving the following constrained optimization problem:
$$\min{\lambda_1\parallel\psi(m_n)\parallel_1}+\lambda_2\parallel\nabla(m_n)\parallel_1$$
$$subj. to \parallel(G-I)(m_n)\parallel_2^2=0,$$
$$\parallel F_{p_n}(m_n)-y_n\parallel_2^2$$
Here $$$y_n$$$ is the acquired undersampled data, $$$F_{p_n}$$$ is the partial Fourier operator, $$$m_n$$$ is the reconstruction for the $$$n^{th}$$$ phase-cycled image, $$$G$$$ is the aggregate interpolation operator, $$$I$$$ is the identity operator, $$$\lambda_1$$$ is the sparsity-penalty weight with $$$\psi$$$ representing wavelet-transform operator, and $$$\lambda_2$$$ is the total-variation (TV) penalty weight with $$$\nabla$$$ representing finite differences operator. The above optimization was performed with an alternating projection-onto-sets scheme that iteratively solved several subproblems: calibration-consistency, data consistency, sparsity and TV projections. The calibration consistency was enforced via SPIRiT model7, with a constant kernel size of 11x11 and Tikhonov regularization parameter as 0.01. Data consistency was enforced by replacing reconstructed data with acquired data in each iteration.
To determine $$$\lambda_1$$$ prior to each sparsity projection, data were analyzed using a framework based on Stein’s unbiased risk estimator5. Hundred linearly spaced threshold values were tested in the range [2x10-5 2x10-2] to obtain risk estimates. The wavelet threshold that minimized the estimated risk was selected for each acquisition separately. The sparsity projection was implemented through soft-thresholding.
To determine $$$\lambda_2$$$ prior to each TV projection, the image for each acquisition was first smoothed by a Gaussians filter, with standard deviation of $$$\sigma=8$$$ and length of 21. The distribution of local variation was estimated using this smoothed image. The TV penalty weight was selected as one-third of the median local variation. The TV projection was implemented via a fast-clipping algorithm6.
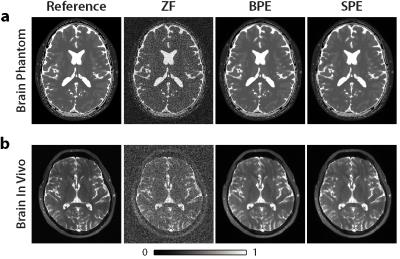
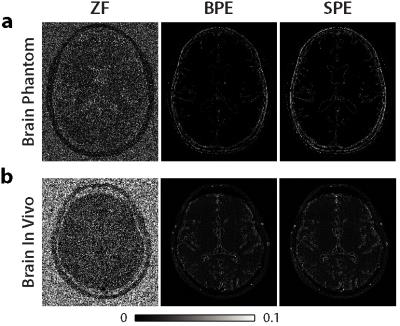
To evaluate the proposed framework, a realistic brain phantom and in vivo brain datasets were used. Both datasets were undersampled by R=8 and acquired with phase increments $$$\Delta\phi=2\pi(0:1:(N-1))/N$$$, where N=8. Zero-filled Fourier (ZF), brute-force profile-encoding (BPE) reconstructions were also implemented. In BPE, PE reconstructions with 20 different linearly spaced sparsity and TV penalty weights were obtained. The penalty weights were varied in ranges [5x10-5 1x10-2] and [1x10-6 3x10-3] for sparsity and TV penalty weights respectively. The reconstruction with best performance among these 4000 reconstructions was selected as the final reconstruction. BPE and SPE reconstructions used 30 iterations.
Reconstructions were combined with p-norm method (p=4), and subsequently images from separate coils were combined via sum-of-squares. Reconstructions were compared against a reference Fourier reconstruction of N=8 fully-sampled acquisitions.
Results
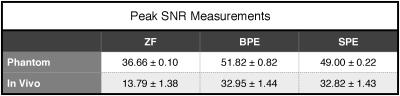
Figures 1 and 2 show the reconstructions and squared-error maps for phantom and in vivo datasets respectively. For both datasets, SPE attains highly similar performance to the brute-force optimized BPE. These observations are supported by the PSNR measurements listed in Table 1. Our results indicate that SPE can automatically tune the penalty weights during profile-encoding reconstructions to maintain near-optimal performance.Conclusion
Here, we evaluated a parameter-free reconstruction approach for accelerated multiple-acquisition bSSFP acquisitions. Compared to conventional reconstructions with hand-picked penalty weights, the proposed method promises greater utility in routine use while maintaining high image quality.Acknowledgements
This work was supported in part by a Marie Curie Actions Career Integration Grant (PCIG13-GA-2013-618101), by a European Molecular Biology Organization Installation Grant (IG 3028), and by a TUBA GEBIP 2015 fellowship.References
1. Scheffler K, Lehnhardt S.Principles and applications of balanced SSFP techniques. Eur. Radiol. 2003;13:2409–2418.
2. Çukur, T. Accelerated Phase-Cycled SSFP Imaging With Compressed Sensing. IEEE Transactions on Medical Imaging 2015; 34(1):107-115; doi: 10.1109/TMI.2014.2346814.
3. Ilicak, E., Senel, L. K., Biyik, E. and Çukur, T. Profile-encoding reconstruction for multiple-acquisition balanced steady-state free precession imaging. Magn. Reson. Med. 2016; doi:10.1002/mrm.26507.
4. Wang, Y., Shao, X., Martin, T., Moeller, S., Yacoub, E. and Wang, D. J.J. Phase-cycled simultaneous multislice balanced SSFP imaging with CAIPIRINHA for efficient banding reduction. Magn. Reson. Med. 2015. doi:10.1002/mrm.26076
5. Khare, K., Hardy, C. J., King, K. F., Turski, P. A. and Marinelli, L. Accelerated MR imaging using compressive sensing with no free parameters. Magn Reson Med. 2012; 68(5):1450–1457. doi:10.1002/mrm.24143.
6. W. Guo and F. Huang. Adaptive total variation based filtering for MRI images with spatially inhomogeneous noise and artifacts. 2009 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Boston, MA, 2009:101-104. doi:10.1109/BI.2009.5192993.
7. Lustig, M. and Pauly, J. M. SPIRiT: Iterative self-consistent parallel imaging reconstruction from arbitrary k-space. Magn. Reson. Med. 2010;64(2):457–471. doi:10.1002/mrm.22428.
Figures