0570
A Fourier Approach to bSSFP Debanding with 3 Phase-Cycled Acquisitions1Radiology, University of British Columbia, Vancouver, BC, Canada
Synopsis
The highly efficient balanced Steady-State Free Precession (bSSFP) sequence has many research and clinical applications. However, it has a peculiar sensitivity to magnetic field inhomogeneity, often resulting in artifacts seen as dark bands. Phase-cycling can generate multiple acquisitions in which the banding is spatially shifted, and subsequently reduced by various algorithms. With 4 acquisitions and an elliptical signal model, it is possible to eliminate the banding by solving the system geometrically, algebraically, or in a combined manner for improved SNR. This work reports a Fourier approach that can effectively reduce the banding using only 3 acquisitions.
Purpose
To develop an efficient and effective method for bSSFP banding artifact reduction with only three phase-cycled acquisitions.Introduction
Owing to its high data acquisition efficiency, superior SNR and resolution, the sequence of balanced Steady-State Free Precession (bSSFP), also termed TrueFISP or FIESTA, keeps finding more research and clinical applications. The bSSFP images are known to have a special type of artifact, observed as dark bands due to magnetic field inhomogengeity. Various algorithms have been proposed to reduce such banding by combining complimentary phase-cycled acquisitions in which the bands are spatially shifted [1-3]. The banding can be eliminated by finding either a geometric solution (GS) or an algebraic solution (AS) from an elliptical signal model with 4 phase-cycled acquisitions [4,5]. The two solutions of GS and AS can be further combined for improved SNR [5]. This work reports another way of using the elliptical signal model. By performing a 3-point Fourier transform, 3 phase-cycled images can be turned into 3 new images containing spatially aligned banding of different amplitudes. These 3 images can be combined using Gradient Energy Minimization (GEM) [6], leading to much reduced banding after destructive interference.Method
The bSSFP signal can be described with the following parametric equation of an ellipse,
$$$I=M\large\frac{1-ae^{i\theta}}{1-b\cos\theta}\normalsize\quad\quad\quad\quad\quad(1)$$$
It can be seen from Eqn.(1) that the signal contains a parallel component $$$P=M/(1-b\cos\theta)$$$ and a rotational component $$$R=-Mae^{i\theta}/(1-b\cos\theta)$$$. For 3 acquisitions with $$$120^{\circ}$$$ phase-cycling, the signals can be written as,
$$$I_{1}=P_{1}+R_{1}\quad\quad\quad\quad\quad\quad(2)$$$
$$$I_{2}=P_{2}+R_{2}E\quad\quad\quad\quad\quad\;(3)$$$
$$$I_{3}=P_{3}+R_{3}E^{2}\quad\quad\quad\quad\;\;\;(4)$$$
where $$$(P_{1},P_{2},P_{3})$$$ and $$$(R_{1},R_{2},R_{3})$$$ are two groups of 3 complex numbers with the same phase or vectors along the same direction, and $$$E=e^{i2\pi/3}$$$ is a phase factor due to phase-cycling. A 3-point Fourier transform can be performed on $$$(I_{1},I_{2},I_{3})$$$ to obtain $$$(S_{1},S_{2},S_{3})$$$ as defined below,
$$$S_{1}\equiv I_{1}+I_{2}+I_{3}=(P_{1}+P_{2}+P_{3})+(R_{1}+R_{2}E+R_{3}E^{2})\quad\quad\quad\quad\quad\quad\qquad(5)$$$
$$$S_{2}\equiv I_{1}+I_{2}E+I_{3}E^{2}=(P_{1}+P_{2}E+P_{3}E^{2})+(R_{1}+P_{2}E^{2}+R_{3}E^{4})\quad\quad\quad\;\;(6)$$$
$$$S_{3}\equiv I_{1}+I_{2}E^{2}+I_{3}E^{4}=(P_{1}+P_{2}E^{2}+P_{3}E^{4})+(R_{1}+R_{2}+R_{3})\quad\quad\quad\qquad(7)$$$
In $$$S_{1}$$$, the 3 vectors $$$(P_{1},P_{2},P_{3})$$$ are all in-phase but the $$$(R_{1},R_{2},R_{3})$$$ are dephased. This $$$S_{1}$$$ is in fact the familiar “complex sum”[1,3] with reduced but still remaining banding; Conversely, in $$$S_{3}$$$, the 3 vectors $$$(R_{1},R_{2},R_{3})$$$ are refocused but the $$$(P_{1},P_{2},P_{3})$$$ are dephased; In $$$S_{2}$$$, both the $$$(P_{1},P_{2},P_{3})$$$ and $$$(R_{1},R_{2},R_{3})$$$ are dephased, in opposite directions. As a result, $$$(S_{1},S_{2},S_{3})$$$ form 3 images containing spatially aligned banding with different amplitudes. A weighted summation can be performed to produce an image with minimized banding due to destructive interference. An algorithm based upon regional Gradient Energy Minimization (GEM) [6] was developed to find the appropriate weighting factors automatically.Three sets of bSSFP data with evenly spaced $$$120^{\circ}$$$ phase-cycling were acquired from a phantom containing metal implant on a 1.5T scanner (Siemens Magneton Avanto, Erlangen, Germany). They were processed off line with codes written in C programing language.
Results
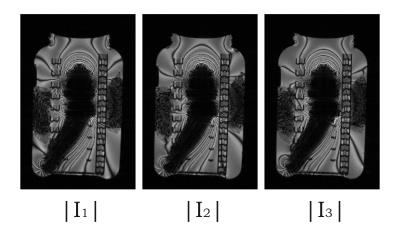
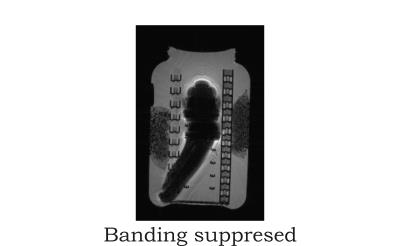
Figure 1 shows the acquired 3 images $$$(I_{1},I_{2},I_{3})$$$ in magnitude format. The busy and intense banding was produced by strong magnetic field inhomogeneity induced by nearby metal implant. The banding was spatially shifted due to phase-cycling among the 3 images. Figure 2 shows the 3 images $$$(S_{1},S_{2},S_{3})$$$ after a 3-point Fourier Transformation according to Eqns.(5-7), in magnitude format. The banding in all 3 images are spatially aligned, but with different amplitude, due to variable rephasing and dephasing configurations of the P and R vectors. The image $$$|S_{2}| $$$ had a weaker average signal intensity due to dephasing of both $$$(P_{1},P_{2},P_{3})$$$ and $$$(R_{1},R_{2},R_{3})$$$ vectors. Figure 3 shows the final output image as a reginally weighted summation of $$$|S_{1}|,|S_{2}|,|S_{3}|$$$ with minimized gradient energy. The banding is hardly visible, demonstrating the effectiveness of this approach.Discussion and conclusion
The bSSFP signal can be decomposed into two vectors, one parallel, the other rotating. With 3-point phase-cycling followed by a 3-point Fourier transform, 3 images can be obtained in which the two vectors have various configurations, either refocused or dephased. In these images, the bands are all spatially aligned but have different amplitudes. Taking advantage of destructive interference, a weighted summation with minimized gradient energy yields a final image free from banding artifact. Efficient and effective bSSFP debanding can be achieved with only 3 phase-cycled acquisitions.Acknowledgements
Support from BCCH Foundation is appreciated.References
[1] Bangerter NK, Hargreaves BA, Vasanawala SS, Pauly JM, Gold GE, Nishimura DG. Analysis of multiple-acquisition SSFP. Magn Reson Med 2004;51:1038–1047.
[2] Elliott AM, Bernstein MA, Ward HA, Lane J, Witte RJ. Nonlinear averaging reconstruction method for phase-cycle SSFP. Magn Reson Imaging 2007;25:359–364.
[3] Lauzon ML, Frayne R. Analytical characterization of RF phase-cycled balanced steady-state free precession. Concept Magn Reson A 2009; 34A:133–143.
[4] Xiang QS, Hoff MN. Banding artifact removal for bSSFP imaging with an elliptical signal model. Magn Reson Med 2014;71:927– 933.
[5] Hoff MN, Andre JB, Xiang QS. Combined Geometric and Algebraic Solutions for Removal of bSSFP Banding Artifacts with Performance Comparisons, Magn Reson Med, First published online : 23 March 2016, DOI: 10.1002/mrm.26150
[6] Chavez S, Xiang QS. Improved Ghost Suppression by Two-Parameter Gradient Energy Minimization. In Proceedings of the 7th Annual Meeting of ISMRM, Philadelphia,USA,1999. Abstract #1999.
Figures