0545

Dictionary-based Reconstruction for Free-Breathing Myocardial T1 Mapping
Jinkyu Kang1,2, Jihye Jang1, Vahid Tarokh2, and Reza Nezafat1

1Department of Medicine, Beth Israel Deaconess Medical Center and Harvard Medical School, Boston, MA, United States, 2School of Engineering and Applied Science, Havard University, Cambridge, MA, United States

Synopsis

In this study, we propose a novel reconstruction framework for myocardial T1 mapping based on a dictionary-based reconstruction algorithm that simultaneously reduces scan time while compensating for respiratory and cardiac-induced motions between different T1-weighted images of T1 mapping sequence.

Introduction

Quantitative myocardial T1 mapping allows for non-invasive assessment of interstitial diffuse fibrosis. In myocardial T1 mapping, series of single shot images are acquired to enable pixel-wise curve fitting of T1 relaxation time. To minimize the impact of cardiac motion during data acquisition for each image, data acquisition is accelerated using conventional acceleration technique such as SENSE or GRAPPA. However, the reduction factor is often limited due to low signal-to-noise ratio which directly impacts measurement precision. In addition, motions between different acquisitions adversely impact T1 map quality. In this study, we propose a novel acceleration technique for myocardial T1 mapping based on dictionary-based reconstruction algorithm that simultaneously reduces the scan time while compensating for respiratory and cardiac induced motions between different T1-weighted images.

Methods

In order to make the T1-weighted images highly compressible1 for acceleration, we propose to design an overcomplete dictionary transform based on Bloch equation by simulating the signal evolutions of T1 mapping sequence with a discrete set of parameters such as T1, T2, TE, TR, flip angle, acquisition time, and the number of phase-encoding lines. From a set $$${\pmb{Y}}$$$ of the training signals generated with a specific range of T1 and T2 values, the overcomplete dictionary $$${\pmb{D}}$$$ is designed such that it simultaneously achieves sparse signal representation and minimizes the approximation error by solving the following optimization problem:

$$\min_{\pmb{D}}\parallel {\pmb{Y}}-{\pmb{D}}{\pmb{X}} \parallel_F^2 \,\,\,\,\,\,\, \text{s.t.} \,\,\,\, \parallel {\pmb{x}}_i \parallel_0 ≤ L \,\,\,\,\,\, \text{for} \,\,\,\,\, ∀\,i,$$

where $$${\pmb{X}}$$$ collects all of the sparse representation $$${\pmb{x}}_i$$$ for i-th training signal as $$${\pmb{X}} = [{\pmb{x}}_1, \dots, {\pmb{x}}_K]$$$ with the number $$$K$$$ of training signals. Here, the dictionary $$${\pmb{D}}$$$ is obtained with sparsity constraint $$$L$$$ based on the K-singular value decomposition (K-SVD) method2 which leads to the optimal possible representation given the set of training signals. Accordingly, the designed dictionary transform provides the optimal approximation of the acquired T1-weighted images that compensates for the motion and aliasing artifacts. In the design of dictionary with $$$K=5000$$$ and $$$L=10$$$, a training set was generated with a range of $$$T_1 \in [50:5:2000]$$$ms and $$$T_2 \in [10:2:200]$$$ms.

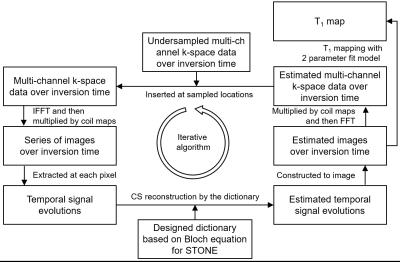
The reconstruction steps are summarized in Fig. 1. In each iteration, multi-channel k-space data were inverse Fourier-transformed and combined by coil sensitivity maps to the image domain for fewer aliasing artifacts. The signal evolutions extracted at each pixel were reconstructed by estimating the sparse representation in the designed dictionary by which the aliasing and cardiac motion artifacts were compensated3. With the image series constructed from the estimated signal evolutions, multi-channel k-space data were computed by multiplying the coil map and performing Fourier transform. Finally, the undersampled k-space data were reinserted into the reconstructed k-space data at the undersampled locations and the result was passed to the next iteration.

To evaluate the performance of the proposed reconstruction frame-work, T1 maps were acquired using Slice-interleaved T1 (STONE) sequence4 with fully-sampled images in both phantom and healthy adult subject. Imaging was performed using a 1.5 T Philips Achieva scanner with a 32 channel cardiac coil array. In phantom study, the imaging parameters were as follows: TR/TE/α=2.45ms/1.23ms/70˚, FOV=277×277mm2, voxel size=2×2×8mm3, 120 phase-encoding lines, 10 linear ramp-up pulses, balanced steady-state free precession readout. In in-vivo study, the imaging parameters were similar except for TR/TE=2.77ms/1.38ms. T1 maps were calculated by using the two-parameter fit model. We performed retrospective undersampling with various reduction factors R in which the acquired fully-sampled data on Cartesian grids were undersampled by keeping the center 11 ky lines and randomly selecting outer ky lines based on a zero-mean Gaussian distribution.

Results

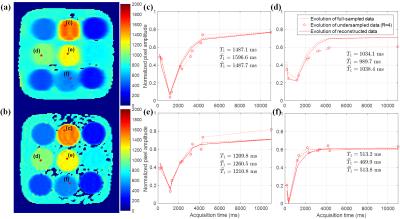
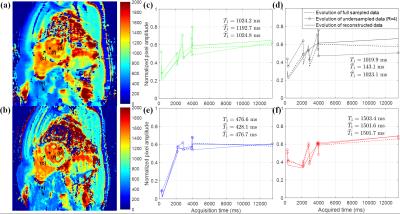
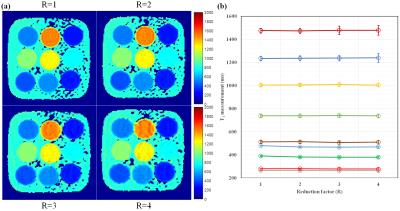
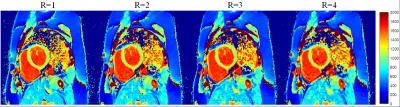
Fig. 2 and 3 show the signal evolutions for 11 T1-weighted images of fully-sampled, undersampled (R=4), and reconstructed data in example voxels in phantom and in-vivo data, respectively. In Fig. 2, the normalized root-mean-square errors (NRMSEs) between signal evolutions of fully-sampled data and reconstructed data are calculated as 0.0717 (c), 0.0632 (d), 0.0659 (e), and 0.0717 (f). Fig. 4 shows T1 maps from reconstructed data, and the T1 measurement and precision in each vial over the reduction factors in phantom. Fig. 5 shows example in-vivo T1 maps with the various reduction factors. The mean T1 values were 1041.3$$$\pm$$$68.36, 1044.1$$$\pm$$$66.16, 1044.3$$$\pm$$$63.24, and 1044.5$$$\pm$$$65.14ms for R=1, 2, 3, and 4, respectively. The precisions were 83.93$$$\pm$$$37.93, 108.72$$$\pm$$$35.86, 114.68$$$\pm$$$40.04, and 136.26$$$\pm$$$48.36ms for R=1, 2, 3, and 4, respectively.

Conclusion

We investigated a dictionary-based reconstruction method from T1 mapping for simultaneous motion correction and image reconstruction. The reconstruction method leads to accurately estimating the signal recovery in T1-weighted images with artifacts.

Acknowledgements

No acknowledgement found.

References

1. Doneva, M., Börnert, P., Eggers, H., et al. Compressed sensing reconstruction for magnetic resonance parameter mapping. Magnetic Resonance in Medicine, 2010; 64(4): 1114-1120.

2. Aharon, M., Elad, M., Bruckstein, A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation. IEEE Transactions on signal processing, 2006; 54(11): 4311-4322.

3. Ma, D., Gulani, V., Seiberlich, N., et al. Magnetic resonance fingerprinting. Nature, 2013; 495(7440): 187-192.

4. Weingärtner, S., Roujol, S., Akçakaya, M., Basha, T. A., Nezafat, R. Free-breathing multislice native myocardial T1 mapping using the slice-interleaved T1 (STONE) sequence. Magnetic resonance in medicine, 2015; 74(1): 115-124.

Figures

Figure 1: Block diagram of iterative dictionary-based reconstruction algorithm. The multi-channel k-space data over inversion time are converted to the image domain and the multi-channel images are combined by coil sensitivity maps. The temporal signal evolutions extracted at each pixel are denoised by compressed sensing (CS) reconstruction with the designed dictionary. The temporal images from the resulting signal evolutions are multiplied by coil map and reconverted to multi-channel k-space data over inversion time. In the final step, the undersampled k-space data are inserted into the estimated k-space data at undersampled locations and the result is passed to the next iteration.

Figure 2: Phantom T1 maps obtained from undersampled data (R=4) (a) and reconstructed data with the dictionary-based algorithm (b). Temporal signal evolutions from the fully-sampled data (dashed lines), undersampled data with R=4 (dotted lines with circle), and reconstructed data (solid lines) for highlighted pixels (c-f), where $$$T_1$$$, $$${\widetilde{T}}_1$$$, and $$${\widehat{T}}_1$$$ are denoted as T1 measurements obtained from fully-sampled, undersampled, and reconstructed data, respectively. In (c), (d), (e), and (f), the NRMSEs between signal evolutions of fully-sampled data and reconstructed data are 0.0717, 0.0632, 0.0659, and 0.0717, respectively. The dictionary-based reconstruction algorithm leads to a good approximation to fully-sampled data.

Figure 3: Free-breathing T1 maps obtained from undersampled data with reduction factor 4 (a) and reconstructed data with the dictionary-based algorithm (b). Temporal signal evolutions from the fully-sampled data (dashed lines), undersampled data with R=4 (dotted lines with circle), and reconstructed data (solid lines) for myocardium (c), (d), liver (e), and left ventricular blood pool (f), where $$$T_1$$$, $$${\widetilde{T}}_1$$$, and $$${\widehat{T}}_1$$$ are denoted as T1 measurements obtained from fully-sampled, undersampled, and reconstructed data, respectively. The dictionary-based reconstruction considerably reduces the artifacts caused by aliasing and cardiac motion.

Figure 4: Phantom T1 maps with various reduction factors in phantom (a). Phantom results in each vial showing the measurement and precision over the reduction factors (b). The error bars indicate the standard deviations within each region of interest. T1 measurements and standard deviations were measured in each vial as the average values over all 5 repetitions. T1 maps seem to be similar and their measurements are consistent but with increased noise at high reduction factor which causes the higher standard deviations.

Figure 5: Reconstruction results of in-vivo undersampled data in a healthy subject with the reduction factors of R=2, 3, and 4. Across 3 subjects, the mean T1 values in the myocardium were 1041.3$$$\pm$$$68.36, 1044.1$$$\pm$$$66.16, 1044.3$$$\pm$$$63.24, and 1044.5$$$\pm$$$65.14ms for R=1, 2, 3, and 4, respectively. The precisions were 83.93$$$\pm$$$37.93, 108.72$$$\pm$$$35.86, 114.68$$$\pm$$$40.04, and 136.26$$$\pm$$$48.36ms for R=1, 2, 3, and 4, respectively.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0545