0524
3D Multi-band Interleaved DW-EPI with 3D Phase Correction1Department of Diagnostic Radiology, The University of Hong Kong, Hong Kong, Hong Kong, 2The State Key Laboratory of Brain and Cognitive Sciences, The University of Hong Kong, Hong Kong, 3Department of Biomedical Engineering, University of Arizona, Tucson, AZ, United States, 4Brain Imaging and Analysis Center, Duke University Medical Center, Durham, NC, United States
Synopsis
The optimal SNR efficiency of 3D multi-slab multi-shot DWI acquisition can be enabled by using a TR range of 1-2s. However, due to the low feasible slab thickness, the multi-slab acquisition can only achieve limited brain coverage when using a short TR. In this study, we first develop a 3D multi-band (MB) iDW-EPI sequence with MB-EVI-based navigator to increase brain coverage when using optimal TR. Second, we extend 3D-MUSER algorithm, which is proposed in another study, to reconstruct 3D-MB-iDW-EPI data with 3D phase correction. Our preliminary result demonstrates the feasibility of 3D MB DWI with 3D phase correction.
Introduction
3D interleaved diffusion-weighted echo-planar imaging (3D-iDW-EPI) can be used to obtain high-resolution DWI with isotropic voxel size1-3. Recently, in-vivo submillimeter DWI is enabled by using 2D multiplexed sensitivity encoding (2D-MUSE) method4, which can suppress undesired noise amplification associated with conventional parallel imaging reconstruction. To achieve better SNR efficiency, multi-slab acquisition is typically used for covering whole brain. Furthermore, the optimal SNR efficiency for white-matter signal can be achieved by using a TR range of 1-2 sec5. However, due to the low feasible slab thickness1, the multi-slab acquisition can only achieve limited brain coverage when using a short TR. We have thus proposed 3D multiplexed sensitivity encoding and reconstruction (3D-MUSER) in another study to improve feasible slab thickness by enabling 3D phase correction with an echo-volume imaging (EVI) -based navigator6. In this study, we first develop a 3D multi-band iDW-EPI (3D-MB-iDW-EPI) sequence with MB-EVI-based navigator to increase brain coverage. Second, we extend 3D-MUSER algorithm to reconstruct 3D-MB-iDW-EPI data with 3D phase correction for eliminating aliasing artifact due to inter-shot phase variations.Methods
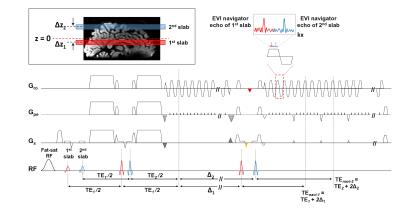
Pulse sequence design: Figure 1 shows a 3D-MB-iDW-EPI sequence using two consecutive RF pulses to simultaneously excite two slabs7. Alternating polarity of second excitation RF pulse between each excitation was used to enable controlled aliasing8. The technical consideration of MB-EVI-based navigator echo is to separate overlapped EVI-based navigator echoes (with R=4) from different slab locations. In order to refrain from using SENSE-based reconstruction of MB-EVI-based navigator echo, we adopted a split-echo scheme to acquire the MB-EVI-based navigator echo by adding a small Gx gradient between two consecutive RF pulses of second refocusing (red triangle in Figure 1). The area of fly-back gradient (orange triangle in Figure 1) was adjusted for aligining the k-space center of navigator echo for each slab, as shown as in FIgure 1.
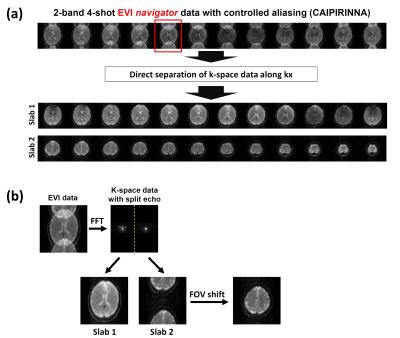
Reconstruction of MB-EVI-based navigator: With implementation of split-echo scheme during acquisition, the k-space signal of MB-EVI-based navigator data can be directly divided into two portions and then reconstructed using the flowchart shown in Figure 2.
Data reconstruction with 3D-MB-MUSER: The 3D-MUSER proposed in another study is a hybrid k-space based reconstruction algorithm with a plane-by-plane reconstruction. The signal equation of a single slab in x-ky-kz space after 1D-FT along x direction can be written as:
$$$S_{\gamma,k_{y|j},k_{z}}=\mathbf{F}_{k_{y|j},k_{z}}\mathbf{\phi}_{k_{y|j},k_{z}}\mathbf{C}_{\gamma}\overline{\rho}$$$ (1).
where $$$\mathbf{F}_{k_{y|j},k_{z}}$$$ denotes an operator of 2D FT along ky|j and kz (ky-kz plane at each x’), $$$\mathbf{\phi}_{k_{y|j},k_{z}}$$$ represents 3D phase variation measured from navigator echo at specific ky|j and kz, Cγ represents the 3D coil sensitivity map of γth coil element, and $$$\overline{\rho}$$$ represents image intensity. With a 2-band excitation, the k-space signal is theoretically a sum of signals from two simultaneously excited slabs, which can be written as:
$$$S_{\gamma,k_{y|j},k_{z}}=\mathbf{F}_{k_{y|j},k_{z}}[\mathbf{\phi}_{k_{y|j},k_{z}}^{z1}\mathbf{C}_{\gamma}^{z1}\overline{\rho}_{z1}+\mathbf{\phi}_{k_{y|j},k_{z}}^{z2}\mathbf{C}_{\gamma}^{z2}\overline{\rho}_{z2}]$$$ (2).
Solving the linear system of 3D-MB-MUSER (Equation 2) by concatenating all signals equations for different coil elements, ky segments, and kz encoding steps can obtain the 3D image volumes of two overlapped slabs. In addition, 3D-MB-MUSER algorithm takes 3D inter-shot phase variations of two overlapped slabs into account, thereby eliminating aliasing artifacts in both of them.
Preliminary test: One set of 3D-MB-iDW-EPI data with 2-band excitation was acquired from a healthy subject at 1.5T MRI scanner (GE HDxt) using an 8-channel head coil. The scan parameters included: slab thickness = 20mm, number of ky segment = 4, number of kz encoding steps = 10, x-y matrix size = 128, TR = 1250 ms, b-value = 800 s/mm2).
Results
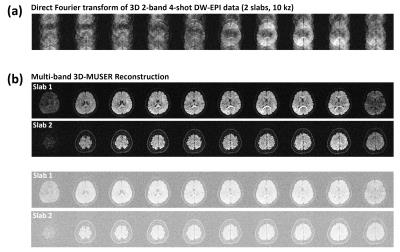
Figure 3a shows MB-EVI-based navigator images reconstructed using direct echo division. Figure 3b shows a representative image (red box in Figure 3a) before and after reconstruction using the flowchart shown in Figure 2. Figure 4 shows the 3D-MB-iDW-EPI data (with 2-band excitation) reconstructed by using either direct FT or 3D-MB-MUSER algorithm.Discussion and Conclusion
Our preliminary result demonstrates the feasibility of 3D-MB-DWI with 3D phase correction. The overlapped 3D-MB-iDW-EPI images can be successfully reconstructed by using 3D-MB-MUSER algorithm, which also eliminates the aliasing artifacts due to inter-shot phase variations present in both slabs. The implementation of split-echo scheme for MB-EVI-based navigator echo reveals a successful measurement of 3D inter-shot phase variations from two simultaneously excited slabs. In conclusion, the implementation of MB technique with 3D-MB-MUSER algorithm is expected to enable optimal SNR efficiency with sufficient brain coverage for 3D-iDW-EPI acquisition.Acknowledgements
No acknowledgement found.References
1. Engstrom M, Skare S. Diffusion-weighted 3D multislab echo planar imaging for high signal-to-noise ratio efficiency and isotropic image resolution. Magn Reson Med 2013;70(6):1507-1514.
2. Frost R, Miller KL, Tijssen RH, Porter DA, Jezzard P. 3D multi-slab diffusion-weighted readout-segmented EPI with real-time cardiac-reordered K-space acquisition. Magn Reson Med 2014;72(6):1565-1579.
3. Van AT, Hernando D, Sutton BP. Motion-induced phase error estimation and correction in 3D diffusion tensor imaging. IEEE Trans Med Imaging 2011;30(11):1933-1940.
4. Chang HC, Sundman M, Petit L, Guhaniyogi S, Chu ML, Petty C, Song AW, Chen NK. Human brain diffusion tensor imaging at submillimeter isotropic resolution on a 3Tesla clinical MRI scanner. Neuroimage 2015;118:667-675.
5. Engstrom M, Martensson M, Avventi E, Skare S. On the signal-to-noise ratio efficiency and slab-banding artifacts in three-dimensional multislab diffusion-weighted echo-planar imaging. Magn Reson Med 2015;73(2):718-725.
6. “Three-Dimensional Multiplexed Sensitivity Encoding and Reconstruction (3D-MUSER): 3D Phase Correction for 3D Multi-shot DWI”, submitted to ISMRM 2017.
7. Chang HC, Guhaniyogi S, Chen NK. Interleaved diffusion-weighted improved by adaptive partial-Fourier and multiband multiplexed sensitivity-encoding reconstruction. Magn Reson Med 2015;73(5):1872-1884.
8. Breuer FA, Blaimer M, Heidemann RM, Mueller MF, Griswold MA, Jakob PM. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med 2005;53(3):684-691.
Figures