0523

Minimum peak power root-flipped gSlider-SMS RF pulses for high-resolution in vivo diffusion imaging
Jun Ma1, Thomas Witzel2, William A Grissom1, and Kawin Setsompop2

1Biomedical Engineering, Vanderbilt University, Nashville, TN, United States, 2Athinoula A. Martinos Center for Biomedical Imaging, Massachusetts General Hospital, Charlestown, MA, United States

Synopsis

gSlider is an RF encoding method that increases SNR in high-resolution diffusion imaging, by repeatedly acquiring high-SNR thick-slab images with distinct through-slice RF phase encoding. The method is currently based on linear-phase RF pulses designed using the inverse scattering transform. However, the high peak power of the associated refocusing pulses requires VERSE to meet practical peak RF amplitude constraints. Here we show that the pulses can be equivalently designed using the SLR algorithm, and that the refocusing pulse can be further root-flipped to minimize its peak amplitude and obviate the use of VERSE, while preserving gSlider encoding and linear-phase spin echoes.

Introduction

The Generalized SLIce Dithered Enhanced Resolution (gSlider)1 method is a volumetric RF-encoded acquisition which improves the SNR efficiency of high resolution diffusion imaging. The method works by acquiring the same slab N times with different excitation phase profiles, and then resolving the slab’s N sub-slices from the high-SNR measurements. In the original method, the excitation-encoding pulses were designed using the inverse scattering method2. However, the associated refocusing pulses had high peak RF amplitudes, especially when multibanded for simultaneous multislice (SMS) imaging. They therefore required VERSE3 for practical implementation, making them sensitive to off-resonance distortion and gradient errors. Here we show how gSlider encoding pulses can be designed using the Shinnar-Le Roux algorithm4 and standard digital filter design codes, and we show that the associated refocusing pulse can be root-flipped5 to minimize its peak amplitude, and the resulting nonlinear refocusing phase profile can be canceled by the excitation pulse to maintain a linear-phase spin echo.

Methods

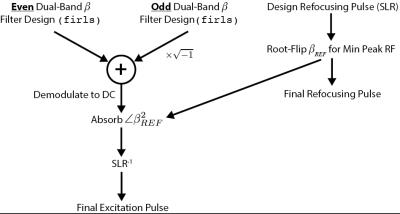
Pulse Design: Figure 1 illustrates the overall design procedure. gSlider slab profiles are generally not symmetric, but conventional least-squares FIR digital filter design codes (in this case, MATLAB’s firls) can only design even or odd filters. To overcome this, both even and odd frequency-offset filters are designed with the same parameters, whose left passbands cancel when summed in quadrature. At the same time, a linear-phase refocusing pulse is designed and root-flipped by exhaustive search. The resulting nonlinear phase profile that will be applied by the root-flipped refocusing pulse is absorbed into the excitation pulses’ beta profiles, before invoking the inverse SLR transform to obtain the excitation pulses. This cancels the refocusing pulse's nonlinear phase and maintains the necessary linear-phase spin echo signals. The phase of the excitation pulses’ alpha polynomials is also absorbed into their beta polynomials for a flatter phase profile. Full pulse design code is available at https://github.com/wgrissom/gSliderRF.

Experiments: The pulses were implemented on the MGH-UCLA Skyra Connectom scanner, with a 64-channel custom receive coil. Data were acquired with a 10 simultaneous slice sagittal acquisition (gSlider × MB = 5 × 2), and ZOOPPA6 was used to suppress neck signal (Rzoom × RGRAPPA = 1.85 × 2 = 3.7). The partial Fourier factor was 6/8, and the TE/TR/b-value were 70ms/5s/1000s/mm2. The final reconstructed matrix size was 158 × 260 × 170, with resolution 660 μm. A head phantom was scanned with both conventional linear-phase gSlider pulses and the root-flipped pulses, and a human volunteer was scanned with the root-flipped pulses, with IRB approval. The excitation pulses were designed with time-bandwidth product 12, slab thickness 3.3 mm, and duration 11 ms. The refocusing pulses were designed with time-bandwidth product 8, slab thickness 3.8 mm, and duration 7.3 ms. The flat-phase pulses were VERSE'd by the pulse sequence to meet peak RF limits.

Results

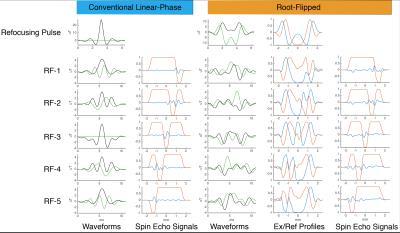
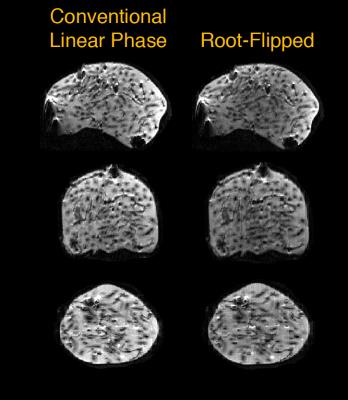
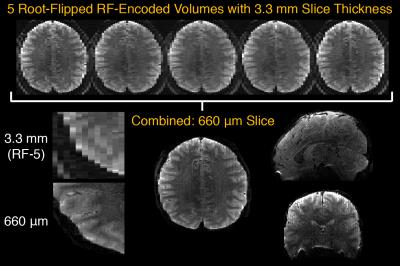
Figure 2 plots conventional linear-phase and root-flipped excitation and refocusing RF pulses and their profiles. The excitation pulses have similar peak amplitudes (~4 μT), but the root-flipped refocusing pulse has ~2.5x lower peak amplitude than the conventional pulse (11 μT versus 27 μT). Figure 3 shows conventional linear phase and root-flipped reconstructions in the phantom, which match closely. Figure 4 shows the individual RF encoded slab images and the high-resolution reconstruction from the in vivo acquisition.

Discussion and Conclusion

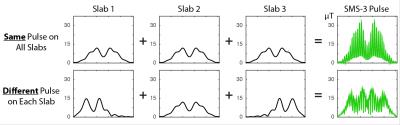
We have demonstrated that gSlider encoding pulses can be designed using the SLR algorithm and conventional digital filter design tools, and that root-flipping can be applied to minimize the peak RF amplitude of the sequence's refocusing pulses, while maintaining the excitation pulses' encoding capability. The root-flipped SLR pulses were validated in 10 simultaneous slice gSlider-SMS acquisitions, where they did not require VERSE to meet the scanner's peak RF limit. With the low MB factor used here (2x) the pulses could be directly summed for SMS imaging without violating the peak RF limit, but Figure 5 shows that constructing MB pulses with multiple root-flipping profiles could help minimize peak RF amplitude for higher MB factors.

Acknowledgements

This work was supported by NIH grants U01MH093765, R01EB020613, R24MH106096, P41EB015896, R01EB016695, R01DA019912, and R21EB018521.

References

1. K. Setsompop, J. Stockmann, Q. Fan, T. Witzel, and L L Wald. Generalized SLIce Dithered Enhanced Resolution Simultaneous MultiSlice (gSlider-SMS) to increase volume encoding, SNR and partition profile fidelity in high-resolution diffusion imaging. In Proceedings 24th Scientific Meeting, International Society for Magnetic Resonance in Medicine, Singapore, page 607, 2016.

2. C. L. Epstein. Minimum energy pulse synthesis via the inverse scattering transform. 2004;167:185– 210.

3. S. Conolly, D. G. Nishimura, A. Macovski, and G. Glover. Variable-rate selective excitation. J Magn Reson, 78:440–458, 1988.

4. J. M. Pauly, P. Le Roux, D. G. Nishimura, and A. Macovski. Parameter relations for the Shinnar-Le Roux selective excitation pulse design algorithm. IEEE Trans Med Imaging, 10:53–65, 1991.

5. A. Sharma, M. S. Lustig, and W. A. Grissom. Root-flipped multiband refocusing pulses. Magn Reson Med, 75(1):227–237, 2016.

6. K. Setsompop, D. A. Feinberg, J. R. Polimeni. Rapid brain MRI acquisition techniques at ultra-high fields. NMR Biomed. 2016. doi: 10.1002/nbm.3478.

Figures

Figure 1: The SLR-based gSlider RF pulse design algorithm, with root-flipping of the refocusing pulse to minimize its peak RF amplitude. A conventional digital filter design code (MATLAB's firls) is used to design even and odd dual-band filters, whose left passbands cancel when summed in quadrature. The refocusing pulse is designed using standard SLR, and is then root-flipped using an exhaustive search of passband root flip combinations. The square of the final refocusing pulse's non-linear phase profile is then absorbed into the excitation pulse's phase profile, to cancel it. Total computation time is ~2.8s on a 3 GHz laptop.

Figure 2: RF Pulses and excitation profiles of conventional linear-phase gSlider refocusing and excitation pulses, and of root-flipped gSlider pulses. The root-flipped refocusing pulse has ~2.5x lower peak RF amplitude, and produces a non-linear phase profile. The square of that phase profile is absorbed into the excitation pulse's profile, resulting in a nonlinear excitation phase that cancels the refocusing pulse's phase in the spin echo signal. Thus, the RF encoded spin echo signals are equivalent for the two pulse types and encoding is maintained.

Figure 3: Reconstructed high resolution (660 μm) diffusion-weighted (b = 1000 s/mm2) phantom images, using conventional linear-phase and root-flipped gSlider pulses. No significant differences are observable between the images.

Figure 4: Acquired diffusion-weighted (b = 1000 s/mm2) in vivo 5x low-resolution (3.3 mm left-right) gSlider images using root-flipped pulses, and reconstructed high resolution (660 μm isotropic) images.

Figure 5: To mitigate peak RF amplitude increases as the MB factor increases, different root-flip patterns can be used for each slab. In this MB factor 3 example, the top row shows the conventional approach of summing identical root-flipped refocusing pulses after modulation and optimal inter-band phase shifting. The peak RF amplitude increased from 12 to 33 μT. The bottom row shows an alternative low-peak power construction using three different root-flip patterns with RF energy concentrated at different times. This results in a 1.4x lower peak amplitude of 23 μT.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0523