0519
Simultaneous Multi-VENC Imaging1Medical Physics in Radiology, German Cancer Research Center, Heidelberg, Germany, 2Institute for Forensic Medicine and Traffic Medicine, University Hospital Heidelberg, Heidelberg, Germany, 3Physikalisch-Technische Bundesanstalt (PTB), Braunschweig and Berlin, Germany
Synopsis
In this work we introduce and investigate the feasibility of "Simultaneous Multi-VENC" (SMV) imaging. This technique is inspired by "spokes" RF pulses used for parallel transmission and by Simultaneous-Multi-Slice (SMS) imaging. SMV enables encoding of a single 2D plane by two or more 2D phase images with different velocity sensitivities, allowing multiple encoding velocities (VENC). Only a single readout is used to acquire all VENC data, which are separated using a standard SMS slice-GRAPPA algorithm. The feasibly of SMV is demonstrated in a flow phantom and in-vivo for three spokes with two different VENC values.
Purpose / Introduction
One-directional 2D phase-contrast MRI is a standard velocity imaging technique used clinically. The velocity is obtained from one (or more) phase differences, thus two (or more) acquisitions are needed, each multiplying the acquisition time. In addition, changes due to e.g. motion between the acquisitions may result in artifacts. In this work we introduce and investigate the feasibility of "Simultaneous Multi-VENC" (SMV) imaging. This technique is inspired by "spokes" RF pulses [1] used for parallel transmission and by Simultaneous-Multi-Slice (SMS) imaging [2]. SMV enables encoding of a single 2D plane by two or more 2D phase images with different velocity sensitivities, allowing multiple encoding velocities (VENC). Only a single readout is used to acquire all velocity encoded data, which are separated using a standard SMS slice-GRAPPA algorithm. The feasibly of SMV is demonstrated in a flow phantom and in-vivo for three spokes with two different VENC values.Theory
According to the superposition principle, in the small tip-angle regime [3] the sum of complex transverse magnetizations $$$M_1,M_2,...,M_N$$$ generated by $$$N$$$ different RF pulses ($$$RF_1,RF_2,...,RF_N$$$) is equal to the magnetization $$$M_{Σ}$$$ generated by a single RF pulse $$$RF_Σ=\sum_{i=1}^{N}RF_i$$$. We make use of this principle for velocity imaging and apply a train of spokes RF pulses (Fig.1) to simultaneously encode the magnetization's velocity through a single 2D slice using multiple different first gradient moments $$$m_1=\int_{t_0}^{t_{end}}G(t)\cdot{t}dt$$$ and, therefore, different $$$VENC$$$ values ($$$VENC=\frac{\pi}{\gamma\left\vert\Delta{m_1}\right\vert}$$$). Each spoke has a characteristic 'isodelay' time point $$$t_0$$$ (typically the RF center), starting from which $$$m_1$$$ is calculated. Compared to standard monopolar spoke pulses, a bipolar rewinder replaces the monopolar rewinder, which allows setting desired moments $$$m_1^i$$$ for each spoke $$$i$$$ (Fig.1). As a result, the transverse magnetization is split into $$$N$$$ portions having different velocity sensitivity.Methods
All acquisitions were performed at 7T (Siemens Healthcare, Erlangen, Germany) using a 28-channel knee coil (Quality Electrodynamics, Mayfield, USA). The excitation pulse of a standard gradient echo (GRE) sequence was replaced by a spokes-train separated by bipolar gradients (Fig.1) in the slice direction. A phantom scan was performed using an agarose-filled cylindrical phantom that contained four water-filled pipes of diameters 4.2/7.8/12.1/15.5mm with water flowing through the two largest pipes. Three spokes were used with $$$m_1^1=23.5\frac{mT}{m}ms^2$$$, $$$m_1^2=13.1\frac{mT}{m}ms^2$$$, $$$m_1^3=0\frac{mT}{m}ms^2$$$ (Fig.1a), leading to $$$VENC_{13}=\frac{\pi}{\gamma\left\vert\Delta{m_1^1-m_1^3}\right\vert}=50\frac{cm}{s}$$$ (low VENC) and $$$VENC_{23}=\frac{\pi}{\gamma\left\vert\Delta{m_1^2-m_1^3}\right\vert}=90\frac{cm}{s}$$$ (high VENC). CAIPIRINHA [4] was applied to shift the field-of-view by 0%/33%/66% for magnetization encoded with $$$m_1^3$$$/$$$m_1^2$$$/$$$m_1^1$$$. Other parameters are listed in Tab.1. Postprocessing was performed in MATLAB (The MathWorks, Natick, USA) as follows: SMV data were dealiased by a slice-GRAPPA [5] algorithm using a separate GRE scan (Tab.1); phase-difference images were corrected for eddy currents (background phase removal) and were noise-masked.
In-vivo data were obtained after obtaining consent according to an IRB approved protocol. Again, 3-spoke SMV excitations were performed with $$$VENC_{23}=70\frac{cm}{s}$$$ and $$$VENC_{13}=50\frac{cm}{s}$$$ targeting a straight portion of the femoral artery. Imaging was performed with cardiac triggering, and a single cardiac phase was obtained during systole (trigger delay=248ms). A B0 map was obtained using a vendor-provided dual-echo GRE sequence (Tab.1) providing a bandwidth of 980Hz. Postprocessing was performed as for the phantom scan, but images were corrected for B0 drifts.
A vendor-provided 2D velocity sequence (Tab.1) was acquired for comparison for both phantom and in-vivo experiments using the high VENCs.
Results
Fig.2 shows magnitude and phase of the aliased and the reconstructed SMV dataset. A clean separation of magnitude and phase was obtained. Corresponding velocity maps are shown in Fig.3b-e for reconstructed high-VENC and low-VENC datasets in comparison to a vendor-provided flow sequence. Corresponding line plots (Fig.3f-h) reveal results comparable to the vendor sequence. Low-VENC data reveal a 1.4-fold lower velocity standard deviation in static areas, indicating lower phase noise. In-vivo results are highlighted in Fig.4 showing high similarity to the vendor-provided sequence with 2% deviation of the peak velocity. Note that fat tissue shows a phase offset caused by the fat signal phase-wrap in the B0 map, which was used for background correction.Discussion
In this work we demonstrate the feasibility of Simultaneous Multi-VENC imaging. Phantom and in-vivo data provide highly similar velocity values compared to the vendor sequence; however, a B0 map with higher bandwidth is needed to also correct for the phase bias within fat tissue. The technique can be extended to encode velocities in other directions, and combinations are feasible as well. Furthermore, simulations demonstrate that this technique is not limited to mono-polar spokes; bi-polar switching can reduce maximum TE values to 6ms for 3 spokes. Furthermore, SMV imaging is not limited to three spokes and can of course be applied at other magnetic field strengthsAcknowledgements
No acknowledgement found.References
[1] Saekho, S., Yip, C.-y., Noll, D. C., Boada, F. E. and Stenger, V. A. (2006), Fast-kz three-dimensional tailored radiofrequency pulse for reduced B1 inhomogeneity. Magn. Reson. Med., 55: 719–724. doi:10.1002/mrm.20840
[2] Larkman, D. J., Hajnal, J. V., Herlihy, A. H., Coutts, G. A., Young, I. R. and Ehnholm, G. (2001), Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J. Magn. Reson. Imaging, 13: 313–317. doi:10.1002/1522-2586(200102)13:2<313::AID-JMRI1045>3.0.CO;2-W
[3] Pauly, J., Nishimura, D., Macovski, A. (1989). A k-space analysis of small-tip-angle excitation. J. Magn. Reson. (1969), 81(1), 43-56.
[4] Breuer, F. A., Blaimer, M., Heidemann, R. M., Mueller, M. F., Griswold, M. A. and Jakob, P. M. (2005), Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn. Reson. Med., 53: 684–691. doi:10.1002/mrm.20401
[5] Setsompop, K., Gagoski, B. A., Polimeni, J. R., Witzel, T., Wedeen, V. J. and Wald, L. L. (2012), Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty. Magn. Reson. Med., 67: 1210–1224. doi:10.1002/mrm.23097
Figures

Table 1:
Sequence parameters for the phantom and in-vivo acquisitions. The gradient echo (GRE) acquisition was used to dealias the SMV dataset. In-vivo acquisitions were performed with cardiac triggering using a vendor-provided ECG system.
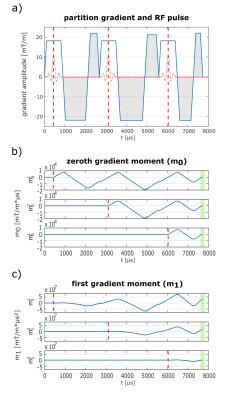
Figure 1:
a) 3-spoke SMV encoding with bipolar gradients (gray shaded) between the spokes. Earlier spokes make use of all following gradients including the following slice selection gradients to encode the velocity in the slice direction. Gradients moments (b+c) are calculated starting from the isodelay time points (dotted red lines in a) until the end of the excitation. Zeroth moments are refocused for all spokes at the end (green shaded area in b). In contrast, first moments are calculated to be non-zero for the first and second spoke (green shaded area in c).
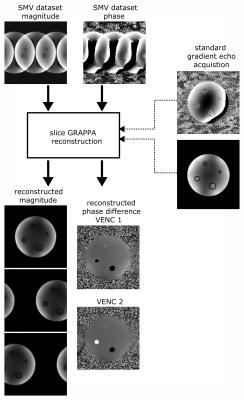
Figure 2:
Data reconstruction scheme. A separate gradient echo dataset is used to dealias the SMV data using a slice-GRAPPA algorithm, providing a clean separation of magnitude and phase. From the dealiased data, high- and low-VENC velocity maps are calculated via phase differences. The high-VENC data can then be used to unwrap the low-VENC data in order to get correct velocity maps with reduced velocity standard deviation.
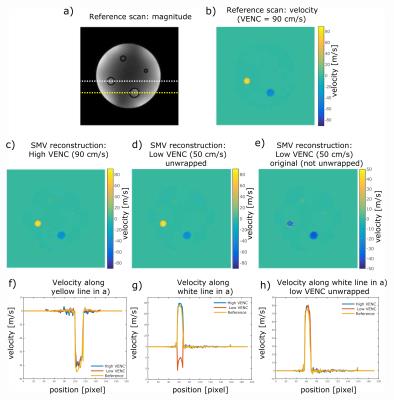
Figure 3:
Velocity maps for reconstructed high-VENC (c) and low-VENC (d+e) datasets in comparison to a vendor-provided flow sequence (b). Corresponding line plots (f-h) reveal results comparable to the vendor sequence. Low-VENC data reveal a velocity standard deviation that is lower by a factor of 1.4 in static areas compared to the high-VENC data, indicating lower phase noise.
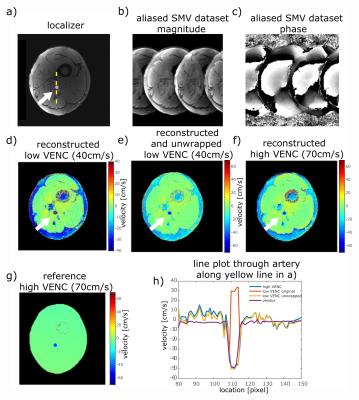
Figure 4:
a) Transverse localizer through the femoral artery (white arrow). b+c) aliased magnitude and phase of the 3-spoke SMV dataset with 3 different $$$m_1$$$ values. d-f) reconstructed low- and high-VENC dataset showing velocity-wraps within the femoral artery in d) that could be recovered using phase unwrapping in e) based on the high-VENC data shown in f). Note that fat is not properly ∆B0 corrected due to the low bandwidth of the B0 acquisition. g) Reference velocity map obtained using the vendor sequence. h) Velocity line plots for reconstructions shown in d-g) along the dashed yellow line shown in a).