0518
Simultaneous Multi-Slice Real-Time Imaging with Radial Multi-Band FLASH and Nonlinear Inverse Reconstruction1Institut für Diagnostische und Interventionelle Radiologie Göttingen, University Medical Center Göttingen, Göttingen, Germany, 2Partner site Göttingen, German Centre for Cardiovascular Research (DZHK), Göttingen, Germany
Synopsis
Simultaneous multi-slice (SMS) MRI allows for the acquisition of several slices at the same time. We propose a novel reconstruction technique for radial SMS MRI based on Regularized Nonlinear Inversion (NLINV). This method does not require a priori knowledge of the coil sensitivities. We present the simultaneous estimation of images and coil sensitivities of two slices of a phantom from 10-fold undersampled data. Image quality is analyzed for different sampling schemes and compared to single-slice acquisitions. Clinical relevance is demonstrated by in-vivo imaging of two slices of a human heart in real-time at a time-resolution of 30.8 ms per frame.
Introduction and Purpose
Increasing imaging speed is of utmost importance in in-vivo MRI. With simultaneous multi-slice (SMS) MRI¹ we can simultaneously acquire several slices of an object, which allows for higher undersampling factors compared to single- or conventional multi-slice measurements by exploiting axial coil sensitivity information. Furthermore, SMS MRI benefits from an inherently increased SNR which contributes to an improved overall image quality.
In SMS MRI, we can use a specific encoding scheme and the spatial encoding information provided by the multi-coil receiver system to disentangle the superposed information of the simultaneously excited slices. Common reconstruction strategies make use of previously estimated coil sensitivities to solve a linear equation. Here, we extend the novel reconstruction approach based on Regularized Nonlinear Inversion (NLINV)2 from Cartesian SMS MRI3 to radial data. For this method no prior knowledge of the coil sensitivities is required, which is particularly beneficial for real-time imaging where coil sensitivities vary due to motion or interactive changes of slice positions.
Method
Phantom
For static measurements we utilize a custom-made phantom made of ABS bricks (LEGO) and pure water (Fig. 1). It is designed such that the proton density of the top and bottom part of the phantom apparently differ. We use this property to demonstrate the capability of SMS-NLINV to disentangle simultaneously excited slices.
SMS sequence
We utilize a 2D radial FLASH sequence with multiband RF excitation pulses generated by a superposition of single-slice pulses. For the acquisition of $$$mb$$$ slices ($$$mb$$$: multi-band factor) we perform $$$mb$$$ (undersampled) measurements and in each measurement $$$p=1,...,mb$$$ the simultaneously excited slices $$$q=1,..,mb$$$ are modulated with a phase (Fourier encoding) $$\Xi_{pq}:=\exp\left(-2\pi i \cdot (p-1)(q-1)/mb\right).$$ We obtain $$$mb$$$ different k-spaces $$$Y_p$$$ (one for each measurement) and define $$$\boldsymbol{Y}:=(Y_1,...,Y_{mb})$$$. For each measurement $$$p$$$ we use complementary radial k-space trajectories to avoid redundancy and to guarantee a maximum coverage of k-space. A schematic of this turn-based sampling strategy for $$$mb=2$$$ slices and 3 spokes is shown in Fig. 2a.
SMS-NLINV reconstruction
$$$\boldsymbol{X}:=(X_1,...,X_{mb})$$$ is the vector we want to reconstruct. Its elements $$$X_q=(m_q,\boldsymbol{c}_q)$$$ contain the object function $$$m_q(x)$$$ and the coil sensitivities $$$\boldsymbol{c}_q(x)$$$ of slice $$$q$$$. We set up the nonlinear equation $$F(\boldsymbol{X})=\boldsymbol{Y},$$ where $$$F$$$ is the forward operator, and solve it with the Iteratively Regularized Gauss-Newton Method (IRGNM).³ The extension to non-Cartesian trajectories is performed by employing a technique that is similar to convolution-based SENSE, where $$\mathcal{F}^{-1}\boldsymbol{P}_{\vec{k}} \mathcal{F}$$ is used as the point spread function.4,5 Here $$$\mathcal{F}$$$ and $$$\mathcal{F}^{-1}$$$ are the Fourier Transform and its inverse and $$$\boldsymbol{P}_\vec{k}$$$ is the projector onto the k-space trajectories.
Experiments
All measurements were conducted on a SIEMENS Skyra 3T scanner. For the static measurements we used a 20-channel head coil. For the in-vivo measurement we utilized 26 channels of a body/spine coil.
Phantom. We measured two slices (base resolution 192, slice thickness 5mm, flip angle 15°, TE 2.0ms, TR 3.1ms) at a distance of 50mm and acquired 31 spokes per measurement (10-fold undersampling), using
(1) two independent single-slice acquisitions,
(2) a SMS acquisition without turn-based trajectory scheme (Fig. 2b),
(3) a SMS acquisition with turn-based trajectory scheme (Fig. 2a).
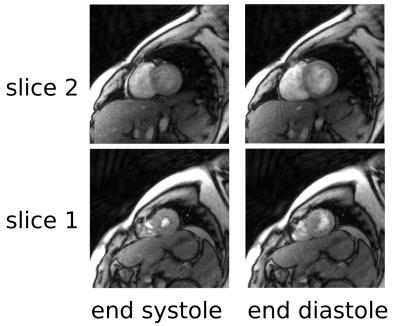
In-vivo. To demonstrate the real-time capability of our reconstruction technique, we simultaneously measured two slices of a human heart (short-axis view) with the turn-based scheme at a time-resolution of 30.8 ms for two slices (7 spokes per measurement, base resolution 160, slice thickness 6mm, flip angle 8°, TE 1.4ms, TR 2.2ms).
Results and Discussion
Phantom. The SMS-NLINV reconstruction can reproduce both slices without significant artifacts (Fig. 3). The SMS scheme (2) gives better results than the single-slice measurements (1) due to the $$$\sqrt{mb}$$$ SNR benefit. The turn-based scheme (3) provides a distinctly higher image quality than the scheme without turns (2). Further preliminary experiments (not depicted) show that the method also works well for higher multi-band factors.
In-vivo. Fig. 4 shows two exemplary frames (end systole and end diastole) for both slices of the real-time in-vivo measurement. The images provide a clinically relevant-time resolution and image quality.
Conclusion and Outlook
In this work, we developed a radial multi-band FLASH sequence and extended the method of Regularized Nonlinear Inversion to radial SMS MRI. We successfully reconstructed highly undersampled SMS data without prior knowledge of the coil sensitivities both for a phantom and in-vivo with real-time-resolution. In the future we will implement the reconstruction algorithm on GPUs5 to allow for online live-reconstructions and evaluate the method in clinical studies.
Acknowledgements
No acknowledgement found.References
1. D. Larkman et al. “Use of multicoil arrays for separation of signal from multiple slices simultaneously excited”. J. Magn. Reson. Imaging 13 (2001), pp. 313–317.
2. M. Uecker et al. “Image reconstruction by regularized nonlinear inversion—joint estimation of coil sensitivities and image content”. Magn. Reson. Med. 60 (2008), pp. 674–682.
3. S. Rosenzweig and M. Uecker. “Reconstruction of multiband MRI data using Regularized Nonlinear Inversion”. In: Proc. Intl. Soc. Mag. Reson. Med. 24 (2016), p. 3259.
4. F. Wajer and K. Pruessmann. "Major speedup of reconstruction for sensitivity encoding with arbitrary trajectories". In: Proc. Intl. Soc. Mag. Reson. Med. 9 (2001), p. 767.
5. M. Uecker et al. “Nonlinear inverse reconstruction for real-time MRI of the human heart using undersampled radial FLASH”. Magn. Reson. Med. 63 (2010), pp. 1456–1462.
Figures
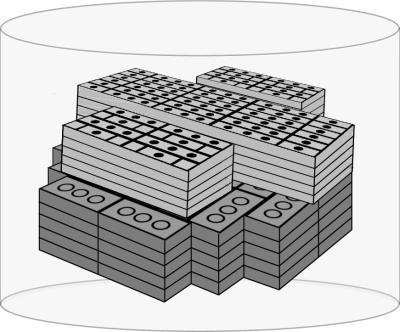
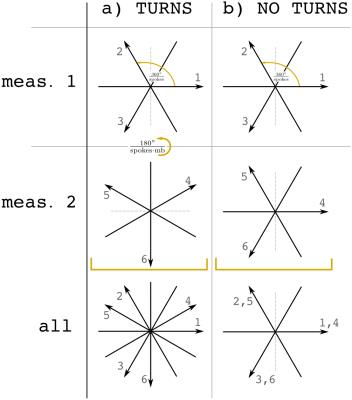
Fig. 2: Schematic of two radial sampling schemes (multi-band factor mb=2 and 3 spokes per measurement). The numbers indicate the order of acquisition.
a) Turn-based scheme: The spokes of all measurements are complementary to guarantee optimal coverage of the k-space.
b) Non-turn-based scheme: For all measurements the same spokes are used.

Fig. 3: Reconstructed slices (2 slices, 50mm slice distance, 5mm slice thickness, 31 spokes per measurement, base resolution 192) acquired from the brick phantom (see Fig. 1). A zoom-in of the inner part as indicated by a red rectangle is shown as inset on the bottom right.
a) Single-slice acquisition and NLINV reconstruction for each slice.
b) SMS acquisition and SMS-NLINV reconstruction (multiband factor mb=2) without turn-based sampling.
c) SMS acquisition and SMS-NLINV reconstruction (mb=2) with turn-based sampling.