0516
A Maximum Likelihood Approach to Simultaneous Multislice Magnetic Resonance Fingerprinting1Martinos Center for Biomedical Imaging, Chalestown, MA, United States, 2Department of Radiology, Harvard Medical School, Boston, MA, United States
Synopsis
Magnetic resonance fingerprinting is an efficient quantitative MRI paradigm, which simultaneously acquires multiple MR tissue parameters. Recently, simultaneous multislice (SMS) acquisition has been used to further speed up MRF experiments. In this abstract, we present a maximum likelihood formulation to enable improved SMS-MRF reconstruction. We further describe an algorithm based on variable splitting, the alternating direction method of multipliers, and the variable projection method to solve the resulting nonlinear and nonconvex optimization problem. Representative results are shown to demonstrate that the proposed method enables more accurate MR tissue parameter maps compared to the recent SMS-MRF approach utilizing direct pattern matching.
Introduction
Magnetic resonance fingerprinting (MRF) [1] is an efficient quantitative imaging paradigm, which simultaneously acquires multiple MR tissue parameters in a single experiment. Although MRF provides an unprecedented imaging speed for single slice imaging, it can still result in clinically unacceptable lengthy acquisitions of up to 20 minutes for volumetric coverage of e.g., the brain. Simultaneous multislice (SMS) imaging [2-4] is an emerging powerful data acquisition methodology, which enables rapid volumetric imaging through acquisition of data from multiple imaging slices simultaneously. Although SMS acquisition has been recently extended to MRF [5, 6], the existing reconstruction framework is still largely based on the conventional approach that utilizes direct pattern matching [1]. In this abstract, we present a maximum likelihood (ML) formulation for SMS-MRF, which models spin physics, SMS data acquisition, and noise statistics. To solve the resulting optimization problem, we develop an algorithm integrating variable splitting, the alternating direction method of multipliers, and the variable projection method. The proposed method is a natural extension of a recent statistical image reconstruction method for single-slice MRF [7], and provides improved accuracy for tissue parameter maps over the competing approach in [5].Method
Denoting $$${\left\{ {I_m^v} \right\}^{}}$$$ as the contrast-weighting images associated with the simultaneously-excited $$$N_s$$$ imaging slices at the $$$m$$$th repetition time, the data model for SMS-MRF can be written as
$${{\bf{d}}_{m,c}} = {{\bf{F}}_m}\sum\limits_{v = 1}^{{N_s}} {{\bf{S}}_c^v} I_m^v + {n_{m,c}},$$
where $$$v$$$ and $$$c$$$ respectively denote the slice and coil index, $$$\mathbf{F}_m$$$ the undersampled Fourier encoding matrix, $$$\mathbf{d}_{m, c}$$$ the measured k-space data, $$$\mathbf{S}_c$$$ the sensitivity maps, and $$$\mathbf{n}_{m, c}$$$ the measurement noise. Furthermore, the contrast-weighting function $$$I_m^v $$$ for each slice can be expressed as $$$I_m^v = \Phi _m^v(T_1^v,T_2^v){\rho ^v}$$$, where $$$ \Phi _m^v(T_1^v,T_2^v)$$$ denotes the contrast-weighting function, and $$$\rho ^v$$$ the spin density. Given that $$$n_{m, c}$$$ is complex Gaussian noise, the maximum likelihood reconstruction can be formulated as
$$ \left\{ {\hat T_1^v,\hat T_2^v,{{\hat \rho }^v}} \right\} = \arg \min \sum\limits_{m = 1}^M {\sum\limits_{c = 1}^{{N_c}} {\left\| {{\bf{d}}_{m,c} - {{\bf{F}}_m}\sum\limits_{v = 1}^{{N_s}} {{\bf{S}}_c^v} \Phi _m^v(T_1^v,T_2^v){\rho ^v}} \right\|_2^2} } .$$
The above formulation leads to a challenging nonlinear and nonconvex optimization problem. Here we extend the algorithm in [7] to solve this problem. More specifically, we use the following variable splitting: $$$g_m^v = \Phi _m^v(T_1^v,T_2^v){\rho ^v}$$$, and $$${h_{m,c}} = \sum\limits_{v = 1}^{{N_s}} {{\bf{S}}_c^vg_m^v} $$$ to form the following augmented Lagrangian functional:
$$ \sum\limits_{m = 1}^M {\sum\limits_{c = 1}^{{N_c}} {\left\| {{{\bf{d}}_{m,c}} - {{\bf{F}}_m}{{\bf{h}}_{m,c}}} \right\|_2^2} } + \frac{{{\mu _h}}}{2}\sum\limits_{m = 1}^M {\sum\limits_{c = 1}^{{N_c}} {\left\| {{{\bf{h}}_{m,c}} - \sum\limits_{v = 1}^{{N_s}} {{\bf{S}}_c^vg_m^v + X_m/{{{\mu _h}}}} } \right\|} } _2^2 + \frac{{{\mu _g}}}{2}\sum\limits_{m = 1}^M {\sum\limits_{v = 1}^{{N_s}} {\left\| {g_m^v - \Phi _m^m\left( {T_1^v,T_2^v} \right){\rho ^v} + Y_m/\mu _g} \right\|_2^2} },$$
where $$$\mathbf{X}_m$$$ and $$$\mathbf{Y}_m$$$ are the Lagrangian multipliers, and $$$\mu_h$$$ and $$$\mu_g$$$ are the penalty parameters. We then use the
alternating minimization scheme to minimize the above functional. In particular, note that the sub-problem with respect to $$$\left\{T_1^v,T_2^v, \rho ^v\right\} $$$ can be solved by the variable projection algorithm as in [7].
Results
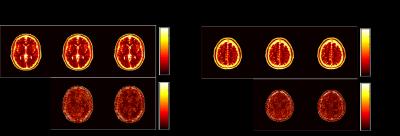
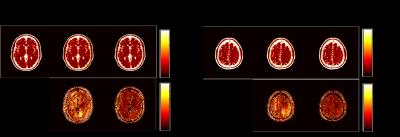
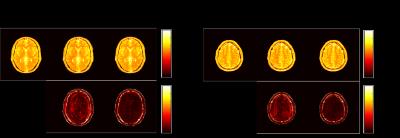
We performed numerical simulations based on the BrainWeb database [8] to evaluate the performance of the proposed method. We simulated the balanced SSFP MRF pulse sequence using Bloch simulations, and created coil sensitivity maps for a 32-channel receiver coils using a Biot-Savart calculator. Two imaging slices with a 40 mm gap were excited with a multiband RF pulse, and the t-blipped SMS-MRF [5] was simulated by adding a 180º degree phase modulation to the second slice at every other TR. The same set of spiral trajectory as in [1] was used, which consists of 48 interleaves. A single spiral interleave was acquired for each TR such that in-plane acceleration is 48. Here, we set the length of an acquisition train as 1000. We performed image reconstruction using the SMS-MRF method in [5] and the proposed method. Figure 1, 2, 3 respectively show the reconstructed T1, T2, and spin density maps, as well as the associated normalized error maps. As can be seen, the proposed method provides more accurate T1, T2, and spin density maps over [5]. The improvement is more pronounced for the T2 and spin density maps, which is consistent with the observations for single-slice MRF reconstruction. Qualitatively, the proposed method reduces ringing and other shading-like artifacts appearing in the T2 and spin density reconstruction for the slice 1.Conclusions
In this abstract, we presented a maximum likelihood formulation for SMS-MRF. We further developed an algorithm to solve the resulting optimization problem. Compared to the conventional approach based on direct pattern matching, the proposed method provides improved accuracy for tissue parameter maps.Acknowledgements
This work was supported in part by the National Institute of Health under Grants: NIH-R01-EB017219, NIHR01-EB017337, NIH-R01-NS089212, NIH-P41-EB015896, NIH-U01-MH093765, and NIH-R24-MH106096.References
[1] D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. Sunshine, J. Duerk, and M. A. Griswold, “Magnetic Resonance Fingerprinting,” Nature, vol. 495, pp. 187-192, 2013.
[2] F. A. Breuer, M. Blaimer, R. M. Heiemann, M. F. Mueller, M. A. Griswold, and P. M. Jakob, “Controlled alising in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging,” Magn. Reson. Med., vol. 53, pp. 684-691, 2005.
[3] K. Setsompop, B. A. Gagoski, J. R. Polimeni, T. Witzel, V. J. Wedeen, L. L. Wald, “Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty,” Magn. Reson. Med., vol. 67, pp. 1210-1224, 2012.
[4] D. A. Feiberg, and K. Setsompop, “Ultra-fast MRI of the human brain with simultaneous multi-slice imaging,” J. Magn. Reson. Med., vol. 229, pp. 90-100, 2013.
[5] H. Ye, D. Ma, Y. Jiang, S. F. Cauley, Y. Du, L. L. Wald, M. A. Griswold, and K. Setsompop, “Accelerating magnetic resonance fingerprinting (MRF) using t-Blipped simultaneous multislice acquisition,” Magn. Reson. Med. vol. 75, pp. 2078-2085, 2016.
[6] H. Ye, S. F. Cauley, B. A. Gagoski, B. Bilgic, D. Ma, Y. Jiang, M. A. Griswold, L. L. Wald, and K. Setsompop, “Simultaneous multislice magnetic resonance fingerprinting (SMS-MRF) with direct spiral slice-GRAPPA (ds-SG) reconstruction,” Magn. Reson. Med., in press. doi: 10.1002/mrm.26271
[7] B. Zhao, K. Setsompop, H. Ye, S. F. Cauley, and L. L. Wald, “Maximum likelihood reconstruction for magnetic resonance fingerprinting,” IEEE Trans. Med. Imag. vol. 35, pp. 1812-1823, 2016.
[8] D. L. Collins, A. P. Zijdenbos, V. Kollokian, J. G. Sled, “Design and construction of a digital brain phantom,” IEEE Trans. Med. Imag., vol.17, pp. 463-468, 2008.
Figures