0478
Massively accelerated VOP compression for population-scale RF safety models1MRI.TOOLS GmbH, Berlin, Germany, 2Berlin Ultrahigh Field Facility (B.U.F.F.), Max Delbrück Center for Molecular Medicine, Germany
Synopsis
Generating high-accuracy VOP sets for safety assessment is hampered by long computation times. We present modifications to the generalized VOP algorithm, significantly increasing its compression capabilities and speed. The novel algorithm is validated and benchmarked on SAR and temperature matrices from nine different coil arrays.
Purpose
Virtual Observation Points (VOPs) have become the de-facto standard for addressing SAR and temperature constraints appearing in parallel transmission (pTx) pulse design, as well as enabling real-time patient safety monitoring during pTx experiments.1,2,3.
To accurately capture SAR variations for broad range of patient anatomies and coil positions, it is imperative to generate VOPs from joint input datasets derived from multiple EMF simulations (using different voxel models), leading to large numbers of input voxels. A low overestimation boundary is desired to minimize unnecessary additional overestimations on top of already applied safety factors. Finally, the number of generated VOPs should not exceed $$$\approx$$$1000 matrices to enable fast pulse calculation and realtime supervision, allowing VOPs to be used in clinical applications of parallel transmission.
This requirement inspired the development of a generalized approach2, which improves upon the original1 in terms of compression, yet suffers from long computation times for large problems and low overestimation bounds, significantly hampering its application for practically sized simulation datasets.
The purpose of this work was to address these shortcomings and enable large scale safety model creation within acceptable timeframes. We investigated the bottlenecks of the existing algorithms and propose massively accelerated VOP compression while concurrently reducing the computational burden. The improved algorithm was evaluated and validated for SAR and temperature matrix datasets for a broad palette of real-world RF coils supporting parallel transmission as well as virtual RF antenna array configurations.
Materials and Methods
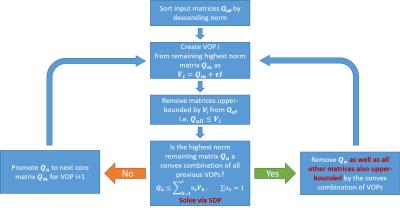
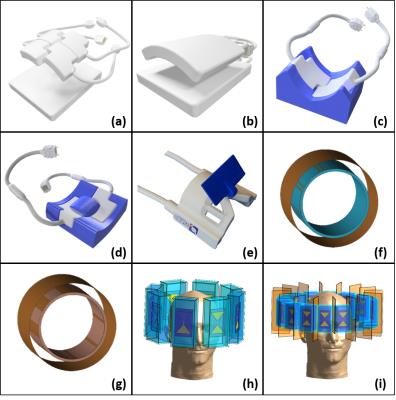
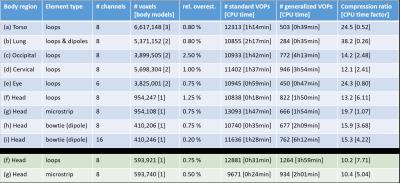
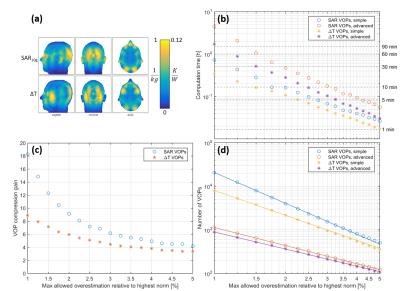
The modified compression algorithm was implemented in MATLAB (The MathWorks, USA), and is outlined in Fig. 1. It was applied to compress the SAR matrices obtained for nine RF arrays between six and sixteen Tx channels (Fig. 2). All coils operated at 300 MHz and were loaded with human voxel models12. Steady-state temperature VOPs were calculated for the two head coil arrays where tissue thermal data was available3. For all models, the overestimation bound was decreased until the original algorithm1 yielded approximately 10,000 VOPs. The final bound was then used in the improved implementation for comparison. Compression performance was evaluated for each coil configuration, with an exemplary focus on one of the head coils for which thermal data was available.Results
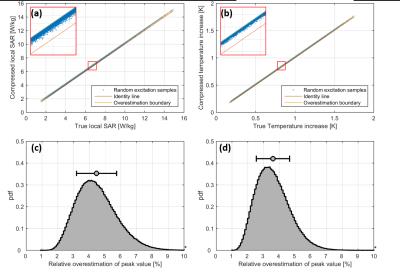
A comparison of the improvements is surveyed in Fig. 3. Compared to the original method1, our proposed algorithm boosts compression by a factor of 13-38 for the SAR VOPs and a factor of 10 for temperature VOPs. This improvement comes at only a moderate increase in computation time (2-4 fold, at worst 7-fold). Contrary to that, even a significant decrease in computation time by up to 75% was observed for the two torso configurations and the eye-coil. A trial over 1,000,000 random excitations comparing the SAR and temperature VOPs is shown in Fig. 4, demonstrating excellent agreement between compressed and full datasets. Results for an overestimation factor sweep is shown in Fig. 5.Discussion
Our modifications to the compression algorithm yield a substantial gain in compression and speed. Compression is gained by exactly solving the linear matrix inequality at the heart of the convex combination problem instead of relying on an iterative approach which is not proven to find a solution if one exists. Speed is gained by additionally testing all matrices against the superpositions previously found by the semidefinite solver.
In the application tests, the algorithm showed remarkably improved compression capabilities across all arrays investigated, with computation times reduced by an order of magnitude compared to previously published results2. Temperature matrices were found to be more compressible than SAR datasets for the same model.
Differences in compressibility between the different coil types can be explained by the strength of E-field correlations inside the different body regions. In a smaller sample, it is possible for higher-order interactions between coil elements since they all cover a large common fraction of the whole volume. In larger samples, such as the torso, the field overlap is comparatively weaker and there are fewer correlations to be captured by individual VOPs. The relatively small eye coil behaves more like two independent 3-channel arrays, explaining the strong compressibility and low computational time.
The fast computation times and low achievable overestimations also enable VOPs to be used in hyperthermia optimizations, where slow speed and overestimation errors often hamper practical use5. The VOP datasets for the two bowtie arrays (Fig.2 h&i) were used for a theoretical performance comparisons in hyperthermia applications6.
In conclusion, our approach enables the large-scale safety model creation required for next generation parallel transmit coils to live up to their full potential.
Acknowledgements
This work was funded (in part, A. K., T.N.) by the EUROSTARS program (heaRT_4_EU, E!9340) and the BMBF (Federal Ministry of Education and Research,Germany, FKZ 01QE1501B).
This work was funded (in part, H.W., T.N.) by the BMBF (Federal Ministry of Education and Research, Germany) FKZ 13GW0102.
References
1. Eichfelder, G., & Gebhardt, M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn. Reson. Med., 66(5), 1468–76.
2. Lee J, et al. Local SAR in parallel transmission pulse design. Magn. Reson. Med. 2012;67:1566–78.
3. Boulant N, et al. (2016) Direct control of the temperature rise in parallel transmission by means of temperature virtual observation points: Simulations at 10.5 tesla. Magn. Reson. Med. 2016;75:249–256.
4. Pendse M, Rutt BK. A Vectorized Formalism for Efficient SAR Computation in Parallel Transmission. Proc. ISMRM 2015:379.
5. Oberacker E. et al. Evaluation and development of applicator designs for simultaneous imaging and adjuvant hyperthermia treatment of glioblastoma multiforme, ISMRM 2017, submitted
6. Michael Grant and Stephen Boyd. CVX: Matlab software for disciplined convex programming, version 2.0 beta. http://cvxr.com/cvx, September 2013.
7. Graessl, A., et al. Modular 32-channel transceiver coil array for cardiac MRI at 7.0T. Magn. Reson. Med., 72(1), 276–90.
8. Waiczies H. et al. 8CH 19F/1H Array for Lung Imaging at 7T (pTX), Proc. ISMRM 2016:3506.
9. Graessl A, et al. Ophthalmic Magnetic Resonance Imaging at 7 T Using a 6-Channel Transceiver Radiofrequency Coil Array in Healthy Subjects and Patients With Intraocular Masses. Invest. Radiol. 2014;49:260–270.
10. Kuehne A. et al. Power balance and loss mechanism analysis in RF transmit coil arrays. Magn. Reson. Med. 2015;74:1165–1176.
11. L. Winter, et al., Design and Evaluation of a Hybrid Radiofrequency Applicator for Magnetic Resonance Imaging and RF Induced Hyperthermia: Electromagnetic Field Simulations up to 14.0 Tesla and Proof-of-Concept at 7.0 Tesla. PLoS One, 2013. 8(4): p. e61661
12. Christ A et al. The Virtual Family--development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys. Med. Biol. 2010;55:N23-38
Figures