Synopsis

Quantitative Magnetization Transfer (qMT) Imaging allows quantification of parameters describing the macromolecular component of tissues, potentially specific for myelin in the central nervous system. To date, applications of qMT in small structures (e.g. the spinal cord) have been hampered by prohibitively long acquisition. We present a framework for robust qMT examinations in small structures. It consists of: a dedicated MT-weighted sequence for reduced field-of-view imaging, explicit modelling of the non-steady state signal, and optimal definition of the sampling scheme. Superiority of the framework compared to a conventional qMT protocol is demonstrated in the healthy spinal cord and in the brainstem.

Purpose

Quantitative Magnetization Transfer (qMT) methods allow the conventionally inaccessible macromolecular component of tissues to be probed. In particular, qMT provides quantification of parameters such as the macromolecular fraction (BPF), macromolecular T₂ (T₂^B), free water T₂ (T₂^F), and free water to macromolecules exchange rate (k_FB), which have proven valuable in assessing myelin integrity in the central nervous system¹.

However, translation of qMT from the brain to small, yet key, structures, such as the spinal cord (SC), a primary location in demyelinating diseases, has not been fully implemented^2,3, as demands of high-resolution and adequate SNR result in prohibitive protocol lengths.

We propose a framework to enable robust assessment of qMT parameters in the SC within a clinically feasible scan time. An MT-weighted reduced Field-of-View echo-planar imaging (EPI) sequence is combined with a dedicated model for unbiased parameter estimation. The sampling scheme is optimized via Cramer-Rao-Lower-Bounds (CRLBs) minimization⁴. Reproducibility of qMT metrics is shown in the healthy SC, and the versatility of the framework for investigating other small structures is demonstrated in the brainstem, crucial for several neurodegenerative diseases and often characterized through MT imaging⁵.

Methods

Image acquisition is performed with ZOOM-EPI⁶. MT sensitization is achieved via off-resonance pulse trains preceding slice excitations. A numerical model based on the coupled Bloch equations⁷ is used for parameter estimation, to account for the non-steady-state nature of the acquisition. In addition to pulse amplitude (B₁) and offset frequency (Δ), effects of pulse duration (τ), inter-pulse gap (Δt), and number of pulses (N) are also modelled.

CRLB theory is used to derive configurations of (B₁,Δ,τ,Δt,N) that maximise precision of (BPF,T₂^F,T₂^B,k_FB), for a fixed number of data-points K=14 (+1 reference image), and under realistic SAR constraints. CRLBs are minimized using a self-organizing migratory algorithm (SOMA)⁸, to produce sets of optimal pairs (Δ,B₁). Remaining parameters (τ,Δt,N) are selected by comparing a posteriori cost function values for optimisations at several combinations of (τ,Δt,N). The cost function is given by the weighted mean of BPF, T₂^B and k_FB CRLBs.

The efficacy of optimization is tested using Monte-Carlo simulations (N=1000 repetitions of Rician noise at SNR=100,50,25,18,12), comparing parameter estimate errors from the optimal protocol against a scheme based on standard steady-state qMT acquisition (i.e. uniform sampling)⁹.

Reproducibility indices (I) of qMT metrics, from a repeated acquisition (three times) on the same subject, are compared between optimal and uniform sampling. For a given parameter p, I(p) is defined as $$$1-\frac{1}{2}(\frac{max(p)-min(p)}{mean(p)})$$$, where I(p)=1 means ideal reproducibility. Qualitative comparison of sampling schemes is performed in the brainstem to highlight the flexibility of the proposed framework.

In vivo imaging is performed on a 3T Philips Achieva system. The full protocol comprises 2 qMT acquisitions (optimal 21:27min, uniform 23:44min), and a shared Inversion-Recovery sequence (8 TIs, TI_min/Δt=150ms/350ms) for T₁ estimation (15:06min); 12 axial slices are acquired at 0.75x0.75x5mm³ resolution in the SC, or at 0.9x0.9x3mm³ in the brainstem.

Results

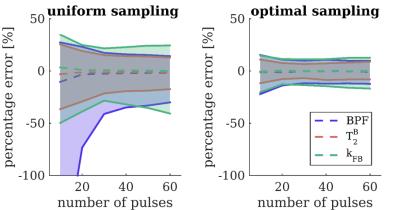
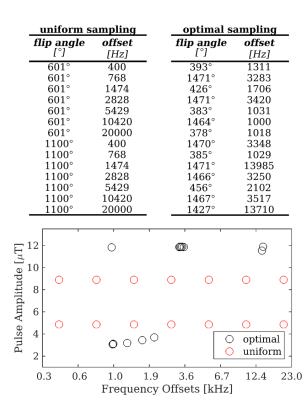
Figure 1 shows optimised protocols producing low estimation errors and having little dependence on N by taking SAR and B₁ limits into account in the optimisation. For N=25, the best configuration for (τ,Δt) was found heuristically at τ/Δt=15ms/15ms. Comparison of optimal (Δ,B₁) sampling at (τ/Δt/N=15ms/15ms/25) and uniform sampling for simulations and in vivo are given in figure 2.

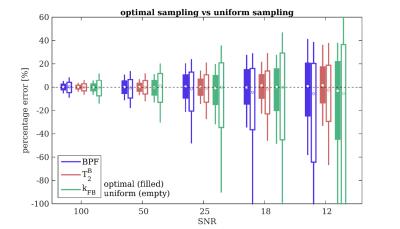
Monte-Carlo simulations demonstrate the superiority of optimal compared to uniform sampling, consistent at different SNR levels (figure 3).

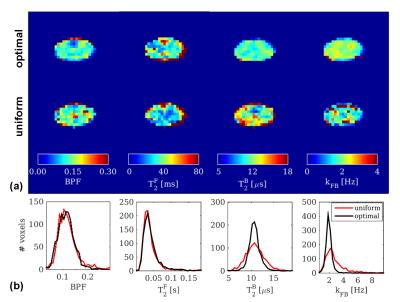
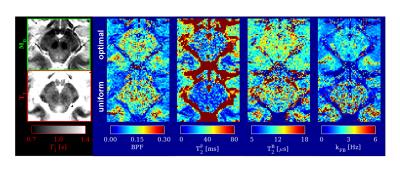
In vivo, qMT parameters in the SC and brainstem (figures 4,5) show reduced variability when obtained from optimal sampling. The improvement over uniform sampling is particularly evident for k_FB. Reproducibility indices (uniform/optimal) in the SC are: I(BPF)=0.74/0.74, I(T₂^F)=0.66/0.62, I(T₂^B)=0.83/0.87, I(k_FB)=0.58/0.82.

Discussion

We combine explicit modelling of the non-steady-state MT signal and protocol optimization to simultaneously improve parameter estimates and shorten scan time compared to conventional sampling.

k_FB is the parameter that benefits the most from optimisation, given its large intrinsic variability as previously reported¹⁰. Reproducibility index did not show improvements in BPF, therefore further investigations are needed to clarify this aspect, including specific protocol optimisations targeting only BPF.

Our framework allows to choose pulse train duty-cycle and duration independently, which we exploit for shorter and more efficient protocols. Here, optimal configuration for (τ,Δt,N) was found empirically, which could lead to suboptimal protocols. The full set of sequence parameters will be optimized simultaneously in future analysis.

The proposed framework is versatile and can be used for any type of localized qMT examination. We have demonstrated its applicability to the brainstem, to delineate differences between the substantia nigra and the surrounding white matter, and provide new complementary information towards the characterization of this structure using MT¹¹.

Acknowledgements

References