Synopsis

The question about the precise value of the proton Larmor frequency in neuronal tissues is a major topic in current research. In this study we present a comprehensive answer for spins moving in magnetically heterogeneous media formed by impermeable susceptibility inclusions. We obtain an analytic result for the mean Larmor frequency in the limit of fast diffusing spins in the space external to the inclusions. This mean frequency explicitly depends on the correlation function of the inclusion. For anisotropic media this results in a nonzero frequency shift, which is confirmed by Monte Carlo simulations.

Purpose

Methods

We consider media with impermeable inclusions with the magnetic susceptibility excess $$$\chi$$$ (Fig.1). The correlation length in the media is $$$l_c$$$, which is close to the inclusion size for a dense packing. The inclusions create a local Larmor frequency shift $$$\Omega(\mathbf{r})$$$, which is the most straightforward to calculate in terms of the Fourier transformed quantities,

$$\Omega(\mathbf{k})=\delta\Omega\,v(\mathbf{k})\,Y_{ab}(\mathbf{k})\,n_am_b\,,\quad\delta\Omega=4\pi\,\gamma B_0\,\chi\,,$$

where $$$v(\mathbf{k})$$$ is the Fourier transform of $$$v(\mathbf{r})$$$, the indicator function that is unity inside and zero outside the susceptibility inclusions, $$$n_a$$$ and $$$m_b$$$ are the unit vectors in the directions of the main field and the induced magnetization, respectively. In media with isotropic magnetic susceptibility $$$m_b=n_b$$$, and in more general case the product $$$\chi\,m_b$$$ should be replaced with $$$\chi_{bc}\,n_c$$$, where $$$\chi_{bc}$$$ is the susceptibility tensor arising on the molecular level⁶. $$$Y_{ab}(\mathbf{k})$$$ is the elementary dipole field,

$$Y_{ab}(\mathbf{k})=\frac{\delta_{ab}}{3}-\frac{k_a k_b}{k^2}\,,$$

and Einstein's convention about summation over repeating indices is used.

In order to disentangle effects of the overall sample shape and the tissue microstructure, we decompose the sample's magnetic field in a far and a near region, where the latter encompasses the transition from the local spin environment to the far region as shown in Fig.2. In the following we consider the field inside a spherical near region, which is shown to be equivalent to cubic simulation media with periodic boundary conditions⁷.

Various media consisting of equally oriented oblate and prolate spheroids (axes radii $$$a=b\neq c$$$) occupying a volume fraction of $$$\zeta=0.15$$$ were generated using a random sequential addition algorithm (Fig.1). Monte Carlo simulations of spin diffusion outside of the impermeable inclusions were performed with the FID signal acquired as the sum of the spins' phase factors. The mean frequency in the near region, $$$\overline\Omega$$$, was obtained as the maximum of the spectral line. Details on medium generation and MC simulations are described elsewhere⁷.

Results

For fast motion each spin senses the effectively averaged field $$$\langle\Omega(\mathbf{r})\rangle$$$ and the NMR signal from the near region (Fig.2B) is completely determined by the mean frequency, $$$\overline\Omega=\langle\Omega\rangle$$$. For the averaging taking place only outside the impermeable inclusions, this quantity is shown to take the form:

$$\overline\Omega=-\frac{\delta\Omega}{1-\zeta}\int\frac{\mathrm{d}^3 k}{(2\pi)^3}\,\Gamma_2(\mathbf{k})\,Y_{ab}(\mathbf{k})\,n_a m_b\,.$$

Here $$$\Gamma_2(\mathbf{k})$$$ is the Fourier transform of the two-point correlation function of the susceptibility inclusions, which is considered in detail elsewhere⁸ and is illustrated in Fig.3,

$$\Gamma_2(\mathbf{r})=\int\frac{\mathrm{d}^3r_0}{V}\,v(\mathbf{r}_0+\mathbf{r})\,v(\mathbf{r}_0)-\zeta^2\,, $$

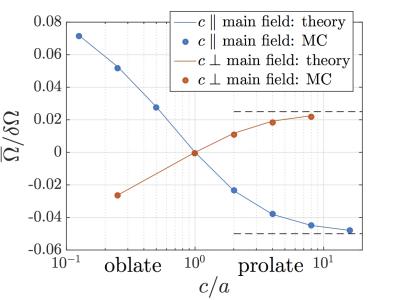
where $$$V$$$ is the sample volume. This revealed dependence on the medium structure is illustrated in Fig.4 in an excellent agreement with Monte Carlo simulations.

For the ideal case of infinitely long, parallel cylinders the above equation is tractable analytically resulting in $$$\overline\Omega/\delta\Omega=\zeta/6$$$ for cylinders orthogonal and $$$\overline\Omega/\delta\Omega=-\zeta/3$$$ for cylinders parallel to the main field. The known zero field for the latter case comes upon addition of the field of the cylindrical far region with a cavity (Fig.2A).

Discussion

The above result is comprehensive for bi-component media. It shows that the Larmor frequency is fully determined by the molecular susceptibility tensor and the inclusions' correlation function. This function is spherically symmetric in isotropic media (for randomly placed spherical and randomly oriented arbitrarily shaped inclusions). In such media the angular integration of the dipole field yields zero as within the classical Lorentz cavity. Anisotropic correlation functions result in a nonzero correction to the Larmor frequency. The anisotropy can arise due to the structural organization of the medium, even for isotropic susceptibility of inclusions' material.

Applied to biological tissues, the considered motional narrowing is a good approximation for the native magnetic susceptibility of cells with sizes of the order of a micrometer. A most probably overestimated upper limit on the controlling parameter of the motional narrowing, $$$\delta\Omega\,l_c^2/D\approx0.2$$$, where $$$D$$$ is the diffusivity, is sufficiently small to justify the approximation.

In biological tissues, the present result is applicable to the extracellular compartment with the most complicated diffusion motion. The intracellular signal should be added to describe the whole tissue⁹.

Acknowledgements

References

1. Duyn JH, van Gelderen P, Li TQ, de Zwart JA, Koretsky AP, Fukunaga M. High-field MRI of brain cortical substructure based on signal phase. Proc Natl Acad Sci USA. 2007; 104:11796–11801.

2. He X, Yablonskiy DA. Biophysical mechanisms of phase contrast in gradient echo MRI. Proc Natl Acad Sci USA. 2009; 106:13558–13563.

3. Duyn JH, Barbara TM. Sphere of Lorentz and Demagnetization Factors in White Matter. Magn Reson Med. 2014; 72:1–3.

4. Yablonskiy DA, He X, Luo J, Sukstanskii AL. Lorentz Sphere Versus Generalized Lorentzian Approach: What Would Lorentz Say About It? Magn Reson Med. 2014; 72:4–7.

5. The original publications have triggered a broad discussion; we apologize for not citing all papers in the abstract format.

6. Liu C. Susceptibility Tensor Imaging. Magn Reson Med. 2010; 63:1471– 1477.

7. Ruh A. Mesoscopic structure through the prism of transverse relaxation. PhD thesis, Faculty of Mathematics and Physics, University of Freiburg. 2016; DOI: 10.6094/UNIFR/11274.

8. Novikov DS, Kiselev VG. Transverse NMR relaxation in magnetically heterogeneous media. J Magn Reson. 2008; 195:33–39.

9. Yablonskiy DA, Sukstanskii AL. Effects of biological tissue structural anisotropy and anisotropy of magnetic susceptibility on the gradient echo MRI signal phase: theoretical background. NMR Biomed. in press.