0455
Stochastic Primal-Dual Optimization for Locally Low-Rank MRI Reconstruction: A Stable Alternative to Cycle Spinning1Radiology, Mayo Clinic, Rochester, MN, United States
Synopsis
Locally low rank (LLR) reconstruction is an effective strategy that has found application across a range of MRI applications. In lieu of processing all overlapping image blocks each iteration, most LLR implementations employ “cycle spinning”, where only a random subset of blocks is processed. Cycle spinning improves efficiency, but may compromise reconstruction convergence and introduce artifacts. We propose a primal-dual algorithm for LLR reconstruction and show that stochastically updating the dual variable provides similar computational advantage as cycle spinning but avoids its primary disadvantages. Reconstruction performance benefits are demonstrated on both a numerical phantom and in vivo.
Purpose
Locally low rank (LLR) reconstruction1,2 is an effective strategy that has proven useful in several MRI applications. Although LLR reconstructions ideally enforce low-rankedness within every overlapping image block per-iteration, that is computationally prohibitive. Thus, most implementations – typically based on parallel proximal gradient3-4 (PPG) iteration – employ “cycle spinning”5,6, wherein only a subset of non-overlapping blocks is processed each iteration. This significantly reduces computational cost, but can cause image intensities to visually oscillate between iterations7, and manifest artifacts at block boundaries. We propose a novel stochastic primal-dual optimization (SPD) strategy for LLR reconstruction that offers the computational advantage of cycle spinning but avoids its instability and artifact issues. After presenting our approach, we demonstrate its performance advantages for calibrationless parallel MRI8,9.
Theory
MRI k-space data is commonly modeled as $$G=A\{F\}+N~[EQ1]$$ where $$$F$$$ is the target image series, $$$A{\cdot}$$$ is the forward operator, and $$$N$$$ is zero-mean Gaussian noise. LLR reconstruction comprises solving the following convex optimization problem:
$$X_{LLR}=\arg\min_{X}\left\{J(X):=\lambda\sum_{b\in\Omega}\|R_{b}X\|_{*}+\|A{X}-G\|_{F}^{2}\right\}~[EQ2]$$
where $$$\Omega$$$ denotes the set of all image blocks, $$$R_{b}$$$ is a block selection operator, $$$\|\cdot\|_{*}$$$ and $$$\|\cdot\|_{F}$$$ are the nuclear and Frobenius norms, and $$$\lambda$$$ is a regularization parameter. EQ1 is generally solved via PPG iteration:
$$X_{t+1}=P_{LLR}\{\tau\lambda\}\{t\}\left(X_{t}-\tau{A^{*}\{A\{X_{t}\}-G\}}\right)~[EQ3]$$
where $$$P_{LLR}\{\gamma\}\{t\}\left(\cdot\right)$$$ is a pseudo-proximal mapping of the LLR penalty, e.g., the blockwise singular value thresholding (SVT)2 operator
$$P_{LLR}\{\gamma\}\{t\}\left(Z\right)=\left(\sum_{b\in\Lambda_{t}}R_{b}^{*}R_{b}\right)^{-1}\sum_{b\in\Lambda_{t}}R_{b}^{*}\mathrm{SVT}_{\tau\lambda/2}\{R_{b}Z\}~[EQ4]$$
and $$$\Delta_{t}$$$ is the blockset considered at iteration $$$t$$$. Although employing $$$\Lambda_{t}=\Omega$$$ is mathematically preferred, in practice $$$\Lambda_{t}$$$ is often defined as a non-overlapping subset of $$$\Omega$$$ that is randomly shifted each $$$t$$$. Cycle spinning offers computational advantage but, as aforementioned, suffers certain limitations. To overcome those, we recast LLR optimization in a manner that stably enables use of stochastic acceleration. To start, recall the nuclear norm dual identity
$$\|Z\|_{*}=\max_{\|Y\|_{2}\leq{1}}\left\{\Re\left\{\mathrm{Tr}\left\{Y^{*}Z\right\}\right\}\right\}~[EQ5]$$
where $$$\|\cdot\|_{2}$$$ denotes the spectral norm. EQ3 can thus be equivalently stated as a primal-dual optimization:
$$X_{LLR}=\arg\min_{X}\max_{\forall{b}\in\Omega,\|Y_{b}\|_{2}\leq{\lambda/2}}\left\{ \sum_{b\in\Omega}2\Re\left\{\mathrm{Tr}\left\{Y_{b}^{*}R_{b}X\right\}\right\}+\|A\{X\}-G\|_{F}^{2}\right\}~[EQ6]$$
where $$$Y_{b}$$$ are dual
variables. Such problems can
be solved using -- amongst other strategies -- Chambolle-Pock iteration10:
$$X_{t+1}=\left(\tau{A}^{*}\{A\}\}+I\right)^{-1}\left(\tau{A^{*}}\{G\}+X_{t}-\sum_{b\in\Omega}R_{b}^{*}Y_{b,y}\right)~[EQ7a]$$
$$Y_{b,t+1}=P_{\|\cdot\|_{2}\leq{\lambda/2}}\left\{Y_{b,t}+\sigma_{b}R_{b}(2X_{t}-X_{t-1})\right\}~[EQ7b]$$
where $$$\tau$$$ and $$$\sigma_{b}$$$ are step sizes, and $$$P_{\|\cdot\|_{2}\leq{\gamma}}\{\cdot\}$$$ is the singular value clipping operator11. Unlike PPG, EQ7 exactly solves EQ1; yet, when all $$$Y_{b}$$$ are updated each iteration, it offers no computational advantage over it. However, analogous to cycle spinning, a random subset (i.e., “mini-batch”) of the dual variables can be updated per-iteration; specifically, EQ7 can be replaced by
$$Y_{b,t+1}=(1-\eta_{b,t})+\eta_{b,t}P_{\|\cdot\|_{2}\leq{\lambda/2}}\left\{Y_{b,t}+\sigma_{b}R_{b}(2X_{t}-X_{t-1})\right\}~[EQ8]$$
where $$$\eta_{b,t}$$$ are Bernoulli random variable. Noting the correspondence between dual variables and blocks, assigning a single $$$\eta$$$ to a set of non-overlapping blocks, with probability reciprocal to set count, is recommended. By casting randomization into the dual domain, this SPD12 strategy for LLR reconstruction is anticipated to exhibit superior convergence behavior and artifact mitigation relative to PPG with cycle spinning.
Methods
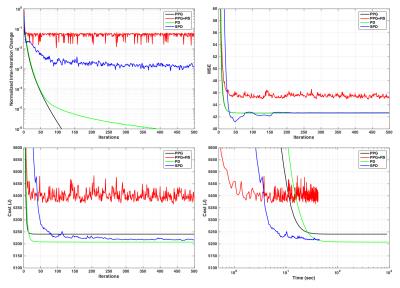
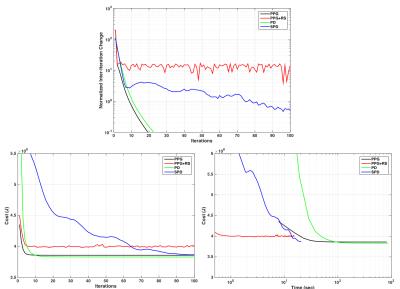
An 8-channel numerical brain phantomREF (128x128) was retrospectively 3x undersampled (variable-density Poisson Disk13), and LLR reconstructed (5x5x8 blocks) using: 1) PPG with fully-overlapping blockset; 2) PPG with randomly shifted non-overlapping blockset (PPG+RS); 3) PD with fully-overlapping blockset; and 4) PD with randomly updated dual variables (SPD). For SPD, updating was performed on dual variable subsets corresponding to non-overlapping blocksets. Each algorithms was executed for 500 iterations, and the primal cost ($$$J(X)$$$) and mean-square-error (MSE) were recorded, as was the inter-iteration image difference Frobenius norm. A healthy volunteer was also scanned at 1.5T (GE Signa, v16) with a 3D-SPGR sequence (FA=20o, TR/TE=15/5ms, FOV=24cm, BW=±31.25kHz, 256x256) and 8-channel head coil. One axial slice of this dataset was retrospectively 3x-undersampled. The same algorithm comparison as above was performed albeit for 100 iterations. All reconstructions were performed in Matlab on a MacBook Pro (2.6GHz Intel Core i7; 16GB memory).Results
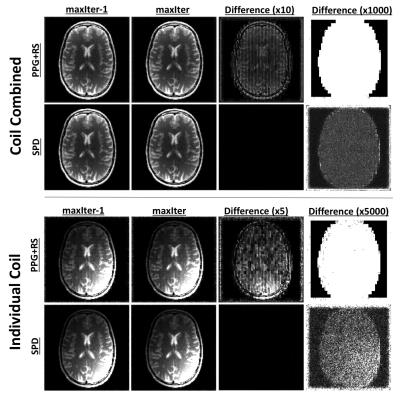
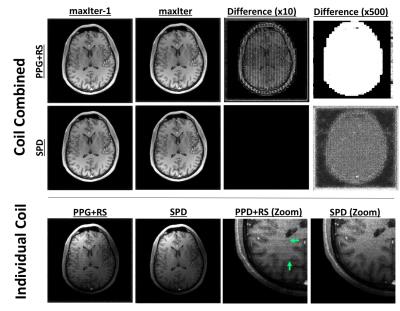
Figures 1 and 3 show convergence plots of various metrics for the numerical phantom and volunteer data. Figures 2 and 4 show both coil combined and individual coil image reconstructions at the second-to-last and last iterations, as well as inter-iteration differences scaled up by different amounts.Discussion
Both PPG and PD demonstrated fast per-iteration but slow per-unit-time convergence. PPGs slight cost underperformance relative to PD can be attributed to its inexact construction4. PPG+RS, as expected, demonstrates low per-iteration cost but poor and unstable convergence, and fails to achieve the same cost reduction as its deterministic counterpart. The high amplitude and structure inter-iteration residuals of PPG+RS are apparent in Figures 2 and 4. Comparatively, SPD exhibits suppressed and non-structured inter-iteration differences, no visually apparent artifact, and computational efficiency mirroring PPG+RS. SPD additionally demonstrates asymptotic cost convergence to PD, highlighting consistency between the optimization models.
Conclusion
Stochastic primal-dual optimization is a stable and computationally efficient alternative to proximal gradient iteration with cycle spinning for LLR reconstruction.Acknowledgements
This work was supported in part by NSF CCF:CIF:Small:1318347 and the Mayo Clinic Discovery Translation Program.References
[1] Trzasko and Manduca. Local versus global low rank promotion in dynamic MRI series reconstruction. Proc. ISMRM 2011;4371.
[2] Candes et al. Unbiased risk estimates for singular value thresholding and spectral estimators. IEEE Trans Sig Proc 2013;61:4643-4657.
[3] Bertsekas. Incremental gradient, subgradient, and proximal methods for convex optimization: A survey. Optimization for Machine Learning 2010:1-38.
[4] Kamilov. Parallel proximal methods for total variation minimization. Proc. ICASSP 2016;4697-4701.
[5] Coifman and Donoho. Translation invariant denoising. Wavelets and Statistics, Springer Lecture Notes, 103, Springer-Verlag, Berlin, 1995.
[6] Figueiredo and Nowak. An EM algorithm for wavelet-based image restoration. IEEE Trans Imag Proc. 2003;12:906-16.
[7] Guerquin-Kern et al. A fast wavelet-based reconstruction method for magnetic resonance imaging. IEEE Trans Med Imag 2011;30:1649-60.
[8] Shin et al. Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion. MRM 2014;72:959-70.
[9] Trzasko and Manduca. CLEAR: Calibration-free parallel imaging using locally low-rank encouraging reconstruction. Proc. ISMRM 2012;517.
[10] Chambolle and Pock. A first-order primal-dual algorithm for convex problems with applications to imaging. J Math Imag Vis 2011;40:120-45.
[11] Cai and Osher. Fast Singular Value Thresholding without Singular Value Decomposition. Methods and Applications of Analysis 2013;20:335-352
[12] Zhang and Xiao. Stochastic primal-dual coordinate method for regularized empirical risk minimization. Proc. ICML 2015;951:2015.
[13] Vasanawala et al. Improved pediatric MR imaging with compressed sensing. Radiology 2010;256:607-16.
Figures