0453
Accelerated 3D Multispectral MRI with Robust Principal Component Analysis for Separation of On and Off-resonance Signals1Electrical Engineering, Stanford University, Stanford, CA, United States, 2Radiology, Stanford University, Stanford, CA, United States
Synopsis
3D multispectral imaging (MSI) corrects most distortion in MRI near metallic implants at the cost of prolonged scan time by phase encoding to resolve slice distortions. However, existing methods to accelerate 3D MSI do not exploit the redundancy of slice-phase encoding for the dominant on-resonance signal. A novel compact representation of 3D-MSI images based on a decomposition of on- and off-resonance via robust principal component analysis (RPCA) is introduced to exploit this redundancy in a calibration and model-free reconstruction and push the current limits of accelerated 3D MSI. A complementary randomized sampling strategy is used to vary undersampling in different spectral bins to enable the separation. Experiments with retrospective and prospective undersampling show comparable image quality between standard MSI images and 2.6-3.4-fold accelerated RPCA and improvement over bin-by-bin compressed sensing reconstruction.
Purpose
3D multispectral imaging (MSI) techniques SEMAC1 and MAVRIC-SL2 enable MRI near metal with substantially reduced distortion by phase-encoding to resolve the slice profile, at the cost of prolonged scan time. Existing methods for constrained 3D MSI offer approximately twofold acceleration, and are limited as they are applied on a bin-by-bin basis3-6. One approach is to explicitly represent the nonlinear relationship between quantitative parameters and undersampled k-space data7. However, model-based reconstruction can be less robust due to modeling errors that are specific to sequence parameters and faces a challenging nonconvex optimization problem. Existing methods also do not exploit the redundancy of slice phase encoding associated with the dominant on-resonance signal. In this work, this redundancy is exploited in a novel calibration and model-free technique to accelerate 3D MSI inspired by robust principal component analysis8 (RPCA), where multispectral images are compactly represented as a sum of rank-one and sparse matrices corresponding to on- and off-resonance signals.Methods
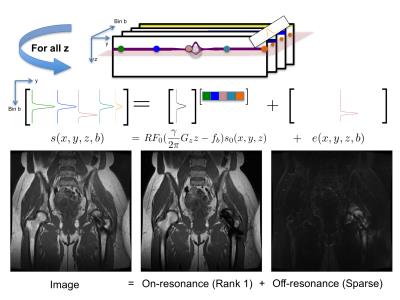
The signal in spectral bin $$$b$$$ and voxel $$$(x,y,z)$$$ is $$$s(x,y,z,b)=RF_0(\frac{\gamma}{2\pi} G_zz−f_b)s_0(x,y,z)+e(x,y,z,b)$$$, where $$$RF_0$$$ is the on-resonance bin RF profile, which weights the on-resonance magnetization $$$s_0$$$, and $$$e$$$ is the off-resonance component. At a fixed $$$z$$$, on-resonance bin profiles at any $$$(x,y)$$$ are spanned by $$$RF_0$$$, and thus, a matrix of bin profiles from different $$$(x,y)$$$ is rank-one plus a spatially sparse error $$$e$$$ due to off-resonance. Figure 1 illustrates this property, showing that the first principal component of this matrix represents on-resonance (93% of the energy) and the residual, off-resonance (Figure 1). Correspondingly, on- and off-resonance components, $$$\hat{L}$$$ and $$$\hat{S}$$$, can be reconstructed from undersampled k-space data, $$$y$$$ by solving $$\hat{L},\hat{S}=\arg\min_{L,S}\|y–\mathcal{F}_u(L+S)\|_2^2+\lambda_1\|TS\|_1+J_L(L) +J_C(L+S)$$ (1), where $$$F_u$$$ is an undersampled Fourier operator, $$$T$$$ is a wavelet transform applied along spatial dimensions, $$$\|\cdot\|_1$$$ is an entry-wise 1 norm, $$$J_L$$$ is a rank-one or low-rank-inducing regularizer, and $$$J_C$$$ is a regularizer previously introduced to extend image-domain calibration-free parallel imaging (CLEAR9) for partial Fourier parallel imaging.10 (1) can be minimized using the alternating direction method of multipliers,11 which can be easily extended with other constraints. We refer to this reconstruction as RPCA. To enable joint reconstruction of bins, a calibrationless variable-density complementary Poisson-disc sampling pattern was used to vary the undersampling in different bins.12
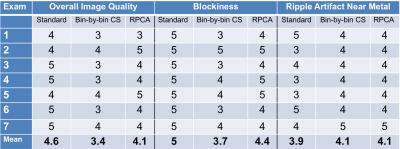
Initial experiments with retrospective undersampling were used to evaluate reconstruction accuracy. Additional experiments were performed with prospective undersampling. PD-weighted hip images in 7 patients were acquired using standard MSI (2×2 autocalibrating parallel imaging and partial Fourier) and prospectively undersampled MSI also with partial Fourier. Scan parameters were 3T; Coronal; TE 6.5ms; TR 4s; FOV 40×40cm2; matrix 384×256; 20-40 sections; 24 bins; radial echo-train view ordering; slice thickness 4mm; ETL 20; half-Fourier; cut k-space corners. Acquisition times were 6-8.3min for standard MSI and 2-3.5 min for accelerated, a 2.6-3.4-fold reduction, 18-24-fold overall. Images from standard and accelerated 3D MSI were evaluated by an experienced MSK radiologist using a 5-point scale (nondiagnostic; limited; diagnostic; good; excellent) in three categories: 1) image quality, 2) blockiness, 3) ripple or pipe-up artifact near metal.
Results
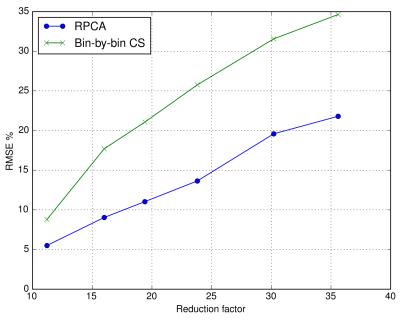
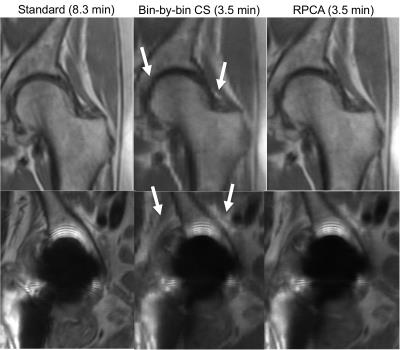
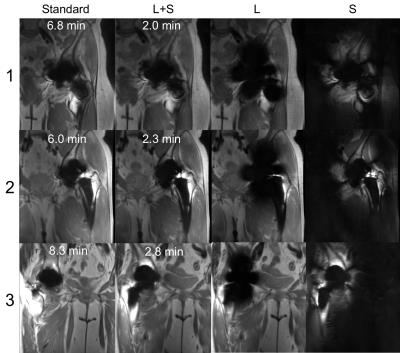
Figure 2 shows reconstruction errors over a range of reduction factors for RPCA and bin-by-bin CS reconstructions. Bin-by-by CS reconstructions used the same penalty terms but without $$$J_L$$$ to induce separation. Artifacts seen in each reconstruction are compared in Figure 3. Figure 4 shows reconstructions from standard and prospectively undersampled 3D MSI acquisitions with separated $$$L$$$ and $$$S$$$ images. RPCA reconstructions and standard MSI showed comparable image quality, while bin-by-bin CS reconstructions had worse scores for image quality and blockiness (Table 1). Reconstructions showed comparable artifact very close to metal.Discussion
In the RPCA approach, multispectral images are compactly represented by a single bin profile and scaling per $$$z$$$ location (rank-one matrix) for voxels that are on-resonance, often the vast majority as shown in Figure 1. This representation is independent of sequence parameters and relies only on separability of the signal. Figure 2 demonstrates the impact of the enhanced sparsity due to the separation of on- and off-resonance. Note that RPCA does not assume spatial smoothness in $$$L$$$ and thus, $$$L$$$ cannot suffer from blocky CS artifacts. Even near metal, these artifacts do not appear in $$$S$$$ due to the enhanced sparsity. Images (Figure 4) and reader scores (Table 1) indicate comparable image quality between standard and accelerated MSI with RPCA, while bin-by-bin CS reconstruction does not provide enough sparsity to reconstruct artifact-free images.Conclusion
3D MSI can be highly accelerated using randomized undersampling that varies between bins and a calibration and model-free reconstruction that represents multispectral images as a sum of rank-one on-resonance and sparse off-resonance components.Acknowledgements
R01 EB017739, research support from GE HealthcareReferences
[1] Lu et. al, MRM 62:66-76, 2009; [2] Koch et. al, MRM 65:71-82, 2011; [3] Worters et. al, JMRI 37:243–248, 2013; [4] Fritz et. al, Investigative Radiology 2016 0:1-11; [5] Otazo et. al, MRM 2016; [6] Sveinsson et. al, MRM 73:662-668, 2015; [7] Shi et. al, ISMRM 2016, p47; [8] Candès E et al. ACM 2011; 58:1-37; [9] Trzasko ISMRM 2012:517 [10] Levine et. al, ISMRM 2015, p3624; [11] Boyd et. al, Foundations and Trends in Machine Learning 3:1-22, 2011; [12] Levine et. al, MRM 2016Figures