0450
Non-ECG First-Pass Myocardial Perfusion T1 Mapping with Low-Rank Tensor Cardiovascular MR Multitasking1Biomedical Imaging Research Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, 2Cedars-Sinai Heart Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, 3Department of Bioengineering, University of California, Los Angeles, Los Angeles, CA, United States, 4Siemens Healthcare, Los Angeles, CA, United States, 5Department of Biomedical Sciences, Cedars-Sinai Medical Center, Los Angeles, CA, United States
Synopsis
Quantitative first-pass myocardial perfusion imaging is a potentially powerful tool for diagnosing coronary artery disease. However, quantification is complicated by ECG misfires and the nonlinear response of signal intensity to contrast agent concentration. Here we propose a method overcoming the curse of dimensionality to simultaneously image cardiac motion, contrast dynamics, and T1 relaxation in 2D and 3D, using a low-rank tensor imaging framework for cardiovascular MR multitasking. This non-ECG, first-pass myocardial perfusion T1 mapping method accounts for the signal intensity nonlinearity, allowing direct quantification of contrast agent concentration at any cardiac phase in any cardiac cycle.
Purpose
First-pass myocardial perfusion imaging is a potentially powerful tool for diagnosing coronary artery disease. However, conventional ECG-triggered methods can misfire, skipping beats and confounding quantification, leading to interest in non-ECG methods1,2. Quantification is further complicated by the nonlinear response of signal intensity to contrast agent concentration, which violates linear shift-invariant flow models. Time-resolved T1 maps could correct for this nonlinearity3, but the curse of dimensionality presents a major barrier for simultaneous imaging of cardiac motion, contrast dynamics, and T1 relaxation. Here we propose a method overcoming this barrier, enabling non-ECG, first-pass myocardial perfusion T1 mapping using a low-rank tensor (LRT) imaging framework for cardiovascular MR multitasking4.Methods
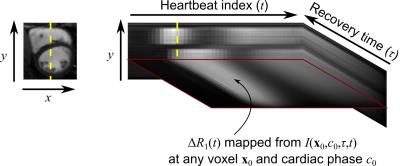
For ECG-free, time-resolved T1 mapping, the desired multidimensional image $$$I(\mathbf{x},c,\tau,t)$$$ is a function of spatial location $$$\mathbf{x}$$$, cardiac phase $$$c$$$, saturation recovery (SR) time $$$\tau$$$, and heartbeat index $$$t$$$. Representing this image as a 4-way tensor $$$\mathcal{A}$$$ with elements $$$A_{ijk\ell}=I(\mathbf{x}_i,c_j,\tau_k,t_\ell)$$$, signal correlation can be exploited by modeling $$$\mathcal{A}$$$ as low-rank4,5, i.e., as the outer product of a core tensor $$$\mathcal{C}$$$ and basis matrices6:$$\mathcal{A}=\mathcal{C}\times_1\mathbf{U_x}\times_2\mathbf{U}_\mathrm{c}\times_3\mathbf{U}_τ\times_4\mathbf{U}_\mathrm{t},\qquad(1)$$or in collapsed form,$$\mathbf{A}_{(1)}=\mathbf{U_xC}_{(1)}(\mathbf{U}_\mathrm{t}\otimes\mathbf{U}_τ\otimes\mathbf{U}_\mathrm{c})^T,\qquad(2)$$where each $$$\mathbf{U}$$$ contains a limited number of basis functions for the corresponding dimension. $$$\mathcal{A}$$$ can then be reconstructed by estimating $$$\mathbf{\Phi}=\mathbf{C}_{(1)}(\mathbf{U}_\mathrm{t}\otimes\mathbf{U}_τ\otimes\mathbf{U}_\mathrm{c})^T$$$ from subspace training data4,5 and then fitting $$$\mathbf{\Phi}$$$ to the remainder of the sparsely sampled data to recover $$$\mathbf{U_x}$$$:$$\hat{\mathbf{U}}_\mathbf{x}=\arg\min_\mathbf{U_x}\|\mathbf{d}-E(\mathbf{U_x\Phi})\|_2^2+R(\mathbf{U_x}),\qquad(3)$$where $$$\mathbf{d}$$$ is the measured data, $$$E(\cdot)$$$ describes multichannel MRI encoding and sampling, and $$$R(\cdot)$$$ is a regularization functional.
The proposed method employed an ECG-free continuous-acquisition SR-FLASH prototype pulse sequence with readouts collected throughout the entire SR period. For 2D, radial acquisition was performed using a golden-angle ordering scheme, interleaved with 0° radial spoke acquisition every other readout as subspace training data. For 3D, stack-of-stars acquisition was performed with golden-angle ordering for the polar coordinates and variable-density Gaussian random sampling for $$$k_z$$$, interleaved with 0° spoke acquisition at $$$k_z=0$$$ every other readout.
Explicit-subspace low-rank matrix imaging7 was first used to obtain an image $$$I(\mathbf{x},t')$$$ with a single “real-time” dimension $$$t'$$$. $$$I(\mathbf{x},t')$$$ depicts the overlapping effects of cardiac motion, T1 recovery, and contrast agent dynamics, allowing image-based cardiac phase identification. The matrix $$$\mathbf{\Phi}$$$ was estimated after LRT completion of the subspace training data4. $$$\hat{\mathbf{U}}_\mathbf{x}$$$ was reconstructed according to Eq. 3, using spatial total variation as the regularization functional $$$R(\cdot)$$$.
To assess repeatability of resting myocardial blood flow (MBF) measurements, n=8 healthy volunteers were imaged on a 3 T Siemens Verio. Pulse sequence parameters were FA=10°, TR/TE=3.6/1.6 ms, FOV=270$$$\times$$$270 mm2, matrix size=160$$$\times$$$160, spatial resolution=1.7$$$\times$$$1.7 mm2, and slice thickness=8 mm. Image reconstruction was performed for 15 cardiac bins and 42 saturation times. Two 0.1 mmol/kg doses of Gadovist were administered 20 to 30 minutes apart. Subjects were instructed to hold their breath for as much of the 45 s scan duration as possible, followed by shallow breathing. To demonstrate the feasibility of 3D imaging, the same process was performed for a healthy volunteer using FA=10°, TR/TE=5.9/2.7 ms, FOV=256$$$\times$$$256$$$\times$$$96 mm3, matrix size=128$$$\times$$$128$$$\times$$$12, spatial resolution=2.0$$$\times$$$2.0$$$\times$$$8.0 mm3.
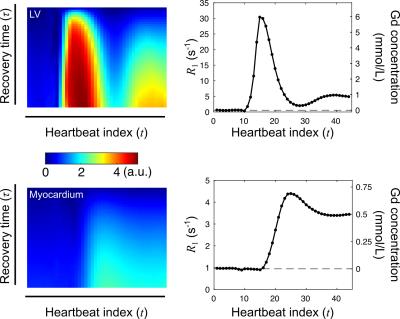
For quantification, $$$T_1(t)$$$ was calculated for the left ventricular (LV) blood pool and six myocardial segments in the 2D images at end-diastole. Contrast agent concentration was calculated as$$Gd(t)={\Delta}R_1(t)/\gamma=\left(\tfrac{1}{T_1(t)}-\tfrac{1}{T_1(0)}\right)/\gamma,\qquad(4)$$where $$$\gamma$$$ is the T1 relaxivity of the contrast agent. Fermi deconvolution8 of each myocardial $$$Gd(t)$$$ by the LV $$$Gd(t)$$$ yielded MBF for each myocardial segment.
Results
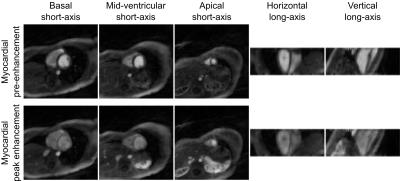
Fig. 1 demonstrates the ability of the proposed method to image multiple cardiac phases as well as the passage of contrast agent. Fig. 2 depicts 3D results demonstrating the ability of the method to scale to whole-heart coverage. Fig. 3 illustrates how with multiple saturation times, signal intensity curves become surfaces; Fig. 4 demonstrates how joint fitting of T1 values at different time points from these surfaces yields $$$Gd(t)$$$. Fig. 5a shows the two-way ANOVA table indicating a nonsignificant difference (p=0.44) between repetitions as well as a nonsignificant difference (p=0.47) between segments, as expected for healthy volunteers. Fig. 5b lists repeatability statistics aggregated over segments. MBF was within the normal range from previous literature9, and the within-segment standard deviation of 0.30 g/mL/min compares favorably with other non-ECG methods10.Conclusions
The proposed method for non-ECG first-pass myocardial perfusion T1 mapping is promising for quantitative myocardial perfusion. The repeatability study shows that 2D MBF measurements are robust to initial contrast agent concentration, demonstrating nonsignificant difference in MBF between first and second boluses. Potential future directions include evaluation of the method for stress perfusion, evaluation of 3D repeatability, and incorporation of motion correction for free-breathing acquisition.Acknowledgements
This work was supported by NIH 1R01HL124649 and NIH T32HL116273.References
1. DiBella EV, Chen L, Schabel MC, et al. Myocardial perfusion acquisition without magnetization preparation or gating. Magn Reson Med. 2012 Mar;67(3):609-13.
2. Sharif B, Dharmakumar R, Arsanjani R, et al. Non-ECG-gated myocardial perfusion MRI using continuous magnetization-driven radial sampling. Magn Reson Med. 2014 Dec;72(6):1620-8.
3. Chen D, Sharif B, Dharmakumar R, et al. Quantification of myocardial blood flow using non-ECG-triggered MR imaging. Magn Reson Med. 2015 Sep;74(3):765-71.
4. Christodoulou AG, Shaw JL, Sharif B, Li D. Proc ISMRM. 2016:867.
5. Liang ZP. Spatiotemporal imaging with partially separable functions. Proc IEEE ISBI. 2007:988-991.
6. Kolda TG, Bader BW. Tensor decompositions and applications. SIAM Rev. 2009 Aug;51(3):455-500.
7. Christodoulou AG, Zhang H, Zhao B, et al. High-resolution cardiovascular MRI by integrating parallel imaging with low-rank and sparse modeling. IEEE Trans Biomed Eng. 2013 Nov;60(11):3083-92.
8. Jerosch-Herold M, Wilke N, Stillman AE, Wilson RF. Magnetic resonance quantification of the myocardial perfusion reserve with a Fermi function model for constrained deconvolution. Med Phys. 1998 Jan;25(1):73-84.
9. Muehling OM, Jerosch-Herold M, Panse P, et al. Regional heterogeneity of myocardial perfusion in healthy human myocardium: assessment with magnetic resonance perfusion imaging. J Cardiovasc Magn Reson. 2004 Jan;6(2):499-507.
10. Likhite D, Suksaranjit P, Adluru G, et al. Interstudy repeatability of self-gated quantitative myocardial perfusion MRI. J Magn Reson Imaging. 2016 Jun;43(6):1369-78.
Figures