0449
Navigator-free EPI ghost correction using low-rank matrix modeling: Theoretical insights and practical improvements1Electrical Engineering, University of Southern California, Los Angeles, CA, United States, 2Radiology, Brigham and Women’s Hospital, Boston, MA, United States, 3Radiology, Harvard Medical School, Boston, MA, United States
Synopsis
While the formation of ghost-free images from EPI data can be a difficult problem, recent low-rank matrix modeling methods have demonstrated promising results. In this abstract, we provide new theoretical insight into these approaches, and show that the low-rank ghost correction optimization problem has infinitely many solutions without using additional constraints. However, we also show that SENSE-like or GRAPPA-like constraints can be successfully used to make the problem well-posed, even for single-channel data. Additionally, we show that substantial performance gains can be achieved over previous low-rank ghost correction implementations by using nonconvex low-rank regularization instead of previous convex approaches.
Purpose
Echo planar imaging (EPI) is subject to Nyquist ghost artifacts due to inconsistencies between adjacent lines of k-space that are acquired with positive and negative (RO+ and RO-) readout gradient polarities. These artifacts are usually addressed by acquiring navigator information to calibrate differences between the polarities1-3. Unfortunately, collecting navigator information adds to experiment duration, and navigator-based methods rely on simplified assumptions and perform inconsistently. Consequently, several navigator-free methods have been proposed4-8, and methods based on LOw-RAnk modeling of local K-Space neighborhoods (LORAKS)8-10 have emerged as especially promising6,7. In this work, we investigate several theoretical and practical aspects of navigator-free LORAKS-based EPI ghost correction.Theory and Methods
EPI collects multiple k-space lines after a single excitation, employing alternating positive and negative readout gradients to quickly traverse k-space. Due to hardware miscalibration, eddy currents, and several other factors, the RO+ and RO- datasets are not directly compatible. While images reconstructed from different polarities have similar magnitudes, they typically have different phase profiles, leading to ghost artifacts if these differences are not corrected before combining the RO+ and RO- data.
Existing LORAKS-based approaches6,7 observe that the RO+ and RO- data can be treated as different channels from a parallel imaging acquisition, similar to dual-polarity GRAPPA11. This is useful because earlier work10,12 showed that subsampled parallel imaging k-space data can be embedded into structured low-rank matrices, and then reconstructed using low-rank matrix recovery. A typical approach is to minimize $$$J(\mathbf{C}(\mathbf{k}))$$$ subject to independent channel-by-channel data consistency constraints, where $$$\mathbf{C}(\mathbf{k})$$$ is a structured matrix formed from the multi-channel k-space data $$$\mathbf{k}$$$, and $$$J(\cdot)$$$ is a regularization functional that encourages $$$\mathbf{C}(\mathbf{k})$$$ to have low-rank.
While LORAKS-based ghost correction has shown promise6,7, we can mathematically prove that the problem with channel-by-channel data consistency constraints is ill-posed. Specifically, there are infinitely many optimal solutions to this problem, and including many undesirable solutions. We omit the details due to space constraints, but the proof relies on the fact that it is possible to spatially-shift the image without violating channel-by-channel k-space data consistency, and without changing the singular values, rank, or nuclear norm (a regularization functional used to encourage low rank6,7) of $$$\mathbf{C}(\mathbf{k})$$$. An illustration is shown in Fig. 1.
This theory implies that additional prior information is necessary for robust LORAKS-based ghost correction. Previous ghost correction work6,7 did not emphasize the importance of such prior information, although one reference7 implicitly incorporated information by using sensitivity maps within the SENSE framework13,14. Using SENSE-like information7,13, LORAKS-based ghost correction is reformulated as $$\hat{\mathbf{k}}=\arg\min_\mathbf{k}\|\mathbf{E}\mathbf{p}-\mathbf{d}\|_2^2+\lambda J(\mathbf{C}(\mathbf{k})),$$ where $$$\mathbf{E}$$$ is the SENSE encoding matrix incorporating sensitivity map information14, $$$\mathbf{d}$$$ is the acquired data, $$$\mathbf{p}$$$ is the SENSE image to be estimated, and $$$\mathbf{k}$$$ is the Fourier transform of $$$\mathbf{p}$$$ after sensitivity weighting.
In this work, we make the novel observation that it is also possible to perform LORAKS-based ghost correction using GRAPPA-like prior information15. The formulation in this case is $$$\|\mathbf{k}-\mathbf{d}\|_2^2+\|\mathbf{N}\mathbf{C}(\mathbf{k})\|_2^2+\lambda J(\mathbf{C}(\mathbf{k}))$$$, where $$$\mathbf{N}$$$ is an estimate of the nullspace of $$$\mathbf{C}(\mathbf{k})$$$ obtained from autocalibration data16. This GRAPPA-like approach is potentially more powerful than the SENSE-like approach, because it does not require explicit estimates of the coil sensitivity---which can be difficult to obtain---and can be used for single-channel EPI data (which features two-channel data when separated by readout polarity).
Finally, we investigated the choice of the regularization functional $$$J(\cdot)$$$, comparing the nuclear norm functional used by recent ghost correction work6,7 against the nonconvex functional used in earlier LORAKS work9,10,13.
Results
Twelve-channel EPI data was acquired using a temporal encoding scheme (PLACE)5 that enables construction of ghost-free fully-sampled RO+ and RO- images (unlike the original PLACE5, we do not subsequently combine polarities). This data was then retrospectively undersampled to simulate EPI datasets with interleaved RO+ and RO- encoding at different acceleration factors.
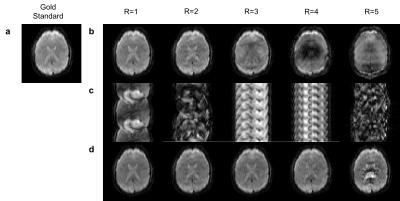
Fig. 2 shows LORAKS-based ghost correction with and without SENSE-based prior information, confirming the power of the LORAKS-based approach and illustrating the importance of prior information. Fig. 3 shows similar results for an in-vivo brain dataset. Fig. 4 shows that LORAKS-based ghost correction of single-channel data is feasible using GRAPPA-based prior information. Finally, Fig. 5 shows the advantages of using nonconvex regularization over nuclear norm regularization.
Discussion and Conclusions
This work provided several new insights into the use of LORAKS-based modeling for EPI ghost correction. We showed that prior information is required for robust LORAKS-based results, and demonstrated that SENSE-like and GRAPPA-like formulations of the problem could both be successful. We also showed that there can be substantial performance advantages to using a nonconvex formulation of LORAKS9,10,13 instead of the nuclear norm6,7.Acknowledgements
This work was supported in part by NSF CAREER award CCF-1350563, and NIH research grants R21-EB022951 and R01-NS089212.References
1. Bruder H, Fischer H, Reinfelder HE, Schmitt F. "Image reconstruction for echo planar imaging with nonequidistant k-space sampling." Magnetic Resonance in Medicine 23:311-323, 1992.
2. Hoge WS, Tan H, Kraft RA. "Robust EPI Nyquist ghost elimination via spatial and temporal encoding." Magnetic Resonance in Medicine 64:1781-1791, 2010.
3. Bernstein MA, King KF, Zhou XJ. Handbook of MRI pulse sequences. Elsevier, 2004.
4. Buonocore MH, Gao L. "Ghost artifact reduction for echo planar imaging using image phase correction." Magnetic Resonance in Medicine 38:89-100, 1997.
5. Xiang QS, Ye FQ. "Correction for geometric distortion and N/2 ghosting in EPI by phase labeling for additional coordinate encoding (PLACE)." Magnetic Resonance in Medicine 57:731-741, 2007.
6. Lee J, Jin KH, Ye JC. "Reference-free single-pass EPI Nyquist ghost correction using annihilating filter-based low rank Hankel matrix (ALOHA)." Magnetic Resonance in Medicine, 2016.
7. Mani M, Jacob M, Kelley D, Magnotta V. "Multi-shot sensitivity-encoded diffusion data recovery using structured low-rank matrix completion (MUSSELS)." Magnetic Resonance in Medicine, 2016.
8. Peterson E, Aksoy M, Maclaren J, Bammer R. "Acquisition-free Nyquist ghost correction for parallel imaging accelerated EPI. " Proc. ISMRM 2015, p. 75.
9. Haldar JP. "Low-rank modeling of local-space neighborhoods (LORAKS) for constrained MRI." IEEE Transactions on Medical Imaging 33:668-681, 2014.
10. Haldar JP, Zhuo J. "P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data." Magnetic Resonance in Medicine, 2015.
11. Hoge WS, Polimeni JR. "Dual-polarity GRAPPA for simultaneous reconstruction and ghost correction of echo planar imaging data." Magnetic Resonance in Medicine, 2015.
12. Shin PJ, Larson PE, Ohliger MA, Elad M, Pauly JM, Vigneron DB, Lustig M. "Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion." Magnetic Resonance in Medicine 72:959-970, 2014.
13. Kim TH, Setsompop K, Haldar JP. "LORAKS makes better SENSE: Phase-constrained partial fourier SENSE reconstruction without phase calibration." Magnetic Resonance in Medicine, 2016.
14. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. "SENSE: sensitivity encoding for fast MRI." Magnetic Resonance in Medicine 42:952-962, 1999.
15. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. "Generalized autocalibrating partially parallel acquisitions (GRAPPA)." Magnetic Resonance in Medicine 47:1202-1210, 2002.
16. Haldar JP. "Autocalibrated LORAKS for fast constrained MRI reconstruction." Proc. IEEE International Symposium on Biomedical Imaging 2015, pp. 910-913.
Figures