0445
Calibrationless Parallel Imaging Reconstruction Using Hankel Tensor Completion (HTC)1Laboratory of Biomedical Imaging and Signal Processing, The University of Hong Kong, Hong Kong, People's Republic of China, 2Department of Electrical and Electronic Engineering, The University of Hong Kong, Hong Kong, People's Republic of China
Synopsis
Autocalibrating parallel imaging requires sufficient autocalibration signals (ACS) for reliable estimation of coil sensitivity. However, this is not feasible in some applications, for example, spectroscopic imaging where matrix size is relatively small. Recent publications (SAKE, P-LORAKS, and ALOHA, etc.) proposed to construct k-space data into block-wise Hankel matrix, and perform parallel imaging reconstruction with low rank matrix completion. In this study, we proposed to construct a block-wise Hankel tensor, and use tensor completion techniques to synthesize the unacquired samples. This method can also be extended to reconstruct multiple slices simultaneously and provide more accurate reconstruction.
Introduction
Autocalibrating parallel imaging requires sufficient autocalibration signals (ACS) for reliable estimation of coil sensitivity. However, this is not feasible in some applications, for example, spectroscopic imaging where matrix size is relatively small. Shin et al. propose to arrange the k-space into a block-wise Hankel matrix, which has an inherently low rank structure. Low rank matrix completion is then applied to synthesize the unacquired samples, and this method is termed simultaneous autocalibrating and k-space estimation (SAKE)1. In SAKE, each kernel contains multiple coils. Block-wise Hankel matrix constructed from multiple coils can also be concatenated side by side (P-LORAKS2 and ALOHA3) based on the assumption that images from different coils share the same support-limited information. In our proposed new method, data from different coils are concatenated as the third dimension, forming a third-order tensor, and tensor completion methods are used to synthesize the unacquired samples. Moreover, if multiple slices are acquired, data from all slices can be stacked to form a tensor of higher order, which can further exploit correlations among adjacent slices.Method
Reconstruction Workflow
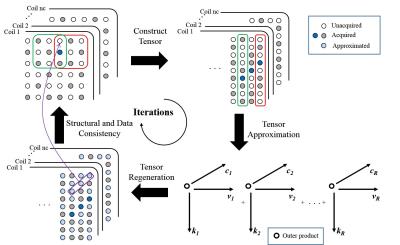
The proposed calibrationless construction using HTC consists of the following steps as illustrated in Figure 1:
(1) Construct Tensor: k-space data from each channel can be structured into a block-wise Hankel matrix, as shown in Figure 1. Data from different channels are stacked to form a 3rd-order tensor, and termed as block-wise Hankel tensor.
(2) Tensor Approximation: Each k-space sample can be fitted from its neighborhood with a compact kernel, indicating that the tensor is inherently low rank. Thus, the tensor formed in this way can be approximated as sum of R rank-1 tensor, where R < nc (coil number) × nk (kernel size). Each rank-1 tensor can be expressed as outer product of three vector, k, c, and v. The approximation can be performed using Alternating Least Square (ALS), which minimizes the least square error between the estimated tensor and original tensor4.
(3) Tensor Regeneration: R rank-1 tensors are summed up to generate the approximated tensor.
(4) Structural and Data Consistency: The k-space is then recovered from the approximated tensor, which enforce structural consistency (Hankel tensor entries from the same k-space sample should be consistent) and data consistency (Hankel tensor entries from acquired samples should match the acquisition).
(5) The unacquired samples are updated iteratively until convergence.
Note that, when multiple slices acquired, the coil sensitivity maps and image structures are usually similar, in which case we can further exploit the correlation among slices. The aforementioned approach can be naturally extended for multi-slice acquisition by concatenating Hankel tensors of different slices to form a 4th-order tensor. Reconstruction with Hankel tensor completion (HTC) can be performed on a single slice or multiple slices simultaneously. These two reconstruction methods are here termed as single-slice HTC (SS-HTC) and multi-slice HTC (MS-HTC), respectively.
Data Acquisition and Retrospective Undersampling
In vivo T2-weighted data were acquired on a 3T scanner using an 8-channel coil with TR/TE=3000/115ms, the data were normalized such that, the image intensity ranges from 0 to 1. Retrospective undersampling was performed by randomly discarding some phase-encoding lines according to a 1-D Poisson disk pattern, which produced a uniform yet randomized sampling. The undersampling factor was set to 3, and 4 phase-encoding lines around k-space center were reserved.
Image Reconstruction
For MS-HTC, data from 6 slices were undersampled independently and reconstructed simultaneously. Considering computation efficacy, MS-HTC, SS-HTC and SAKE were used to recover a 50×50 calibration region, with iteration number set to 100, kernel size set to 6×6, and target rank set to 100, 60, and 60 for MS-HTC, SS-HTC and SAKE, respectively. After that, ESPIRiT applied with the same parameters (2 maps, 20 iterations)5.
Results
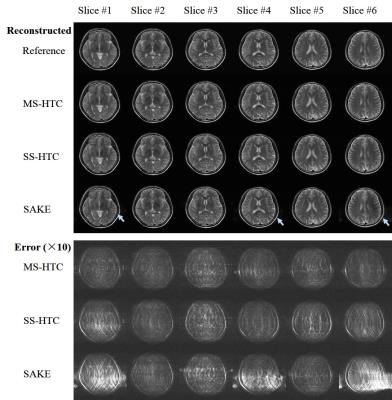
As shown in Figure 2, with SAKE, the reconstructed images still suffered from residual aliasing artifacts, likely due to the inaccurate estimation of calibration region. With SS-HTC, the results were improved significantly. Careful inspection revealed that, with MS-HTC, the reconstructed images exhibited fewer residual aliasing artifacts. The mean residual errors (i.e., difference from the reference images) for SAKE, SS-HTC, MS-HTC were 0.032, 0.027, and 0.025, respectively, indicating that MS-HTC offered ~25% less residual error when compared with SAKE.Discussion and conclusions
We demonstrated that the proposed calibrationless reconstruction with Hankel tensor completion (HTC) method offers a better alternative to SAKE. The proposed new method provides more accurate estimation of unacquired data, thus less residual error. Moreover, it is more flexible. It can be extended to exploit data redundancy across different slices and further improves the calibrationless parallel imaging reconstruction.Acknowledgements
No acknowledgement found.References
[1] P. J. Shin, P. E. Larson, M. A. Ohliger, M. Elad, J. M. Pauly, D. B. Vigneron, et al., "Calibrationless parallel imaging reconstruction based on structured low-rank matrix completion," Magn Reson Med, vol. 72, pp. 959-70, Oct 2014.
[2] J. Zhuo and J. P. Haldar, "P-LORAKS: Low-rank modeling of local k-space neighborhoods with parallel imaging data," in Proc. Int. Soc. Magn. Reson. Med, 2014, p. 745.
[3] D. Lee, K. H. Jin, E. Y. Kim, S. H. Park, and J. C. Ye, "Acceleration of MR parameter mapping using annihilating filter-based low rank hankel matrix (ALOHA)," Magnetic resonance in medicine, 2016.
[4] N. Vervliet, O. Debals, L. Sorber, M. Van Barel, and L. De Lathauwer, "Tensorlab 3.0," 2016.
[5] M. Uecker, P. Lai, M. J. Murphy, P. Virtue, M. Elad, J. M. Pauly, et al., "ESPIRiT-an eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA," Magn Reson Med, May 6 2013.
Figures