0441
Joint Reconstruction of Phase-Cycled Balanced SSFP with Constrained Parallel Imaging1Martinos Center for Biomedical Imaging, Charlestown, MA, United States, 2Siemens Medical Solutions, Charlestown, MA, United States
Synopsis
Balanced SSFP is an SNR-efficient sequence with unique T2/T1 contrast, but suffers from banding artifacts due to B0 sensitivity. These artifacts can be mitigated through RF phase-cycling at a cost of significant increase in scan time. Here, we propose Joint L1-SPIRiT to jointly reconstruct highly accelerated/undersampled phase-cycled images and convert the different banding artifacts of these images into additional spatial encoding. This enables highly accelerated 2D and Simultaneous Multi-Slice imaging, thus mitigating scan time burden of phase-cycled bSSFP while producing banding-free images. In particular, Joint L1-SPIRiT provides around 2-fold decrease in both the average g-factor and RMSE relative to GRAPPA.
Introduction
Balanced steady state free precession (bSSFP) is an SNR-efficient technique that has found widespread use in cardiac, abdominal and brain imaging. Despite being a rapid sequence with unique T2/T1 contrast, it suffers from banding artifacts due to B0 sensitivity. To mitigate these artifacts, multiple image data with different RF phase-cycling that shifts the B0 sensitivity band are acquired and combined through maximum intensity projection (MIP). Such phase-cycling increases scan time, counteracting the inherent efficiency of bSSFP. To alleviate this, parallel imaging [1,2] and Simultaneous Multi-Slice (SMS) [3] have been deployed in phase-cycled bSSFP [4,5] for up to 4-fold acceleration. Moreover, Joint-GRAPPA [6] has recently been proposed to permit joint reconstruction of phase-cycled images and provided improvement over conventional GRAPPA reconstruction.
Herein, we propose Joint L1-SPIRiT, which extends and improves upon Joint-GRAPPA by enforcing consistency across both sampled and estimated k-space and exploiting gradient sparsity. This approach permits: up to 2.5-fold decrease in maximum g-factor, 2.3-fold decrease in average g-factor, and 1.9-fold reduction in RMSE relative to GRAPPA. Such improvement is achieved through Total Variation (TV) regularization together with SPIRiT kernels [2] that are fitted jointly across channels and phase-cycles, analogous to k-t and virtual coil approaches in dynamic and diffusion imaging [7,8].
Matlab code that reproduces the results is available at: bit.ly/2eyWfAT
Methods
Joint L1-SPIRiT creates virtual coils by
stacking phase-cycles along the channel axis, where all coils and all cycles
contribute to the reconstruction of a particular channel. Similar to k-t
acquisition, sampling pattern is shifted across the cycles to provide
complementary k-space coverage. By creating virtual coils out of the
phase-cycles, Joint L1-SPIRiT makes use of intensity and phase modulations due
to B0 inhomogeneity, and converts these artifact sources into useful,
additional spatial encoding. With Joint L1-SPIRiT reconstruction is regularized
by gradient sparsity as follows:
$$\min_{x} \parallel (G-I)x \parallel_2^2 + \lambda \parallel \nabla F^{-1}x \parallel_1 \hspace{5mm} s.t. \hspace{5mm} Dx=y$$
Here $$$x$$$ represents k-space from all coils and cycles, $$$G$$$ are SPIRiT kernels, $$$\nabla$$$ is the gradient operator, $$$F^{-1}$$$ is the inverse Fourier transform, $$$y$$$ denotes sampled data and $$$D$$$ selects acquired samples. The constraint $$$Dx=y$$$ can be absorbed into the data consistency via $$$x=D^{T}y+D_c^T \tilde{x}$$$, where $$$D^T$$$ and $$$D_c^T$$$ insert the acquired and nonacquired samples into the full k-space grid, and $$$\tilde{x}$$$ denotes only the missing samples:
$$\min_{\tilde{x}} \parallel (G-I) D_c^T \tilde{x} +(G-I)D^T y \parallel_2^2 + \lambda \parallel \nabla F^{-1} D^T y+ \nabla F^{-1} D_c^T \tilde{x} \parallel_1$$
Optimization is performed using nonlinear CG [9].
To test Joint L1-SPIRiT, three datasets were acquired on a healthy volunteer at 3T with four phase-cycled bSSFP (0, π/2, π, 3π/2) for the following 2D and SMS cases:
i) 2D abdominal imaging at R=6×: FOV=380×380mm2, mtx=160×160, 5mm slice, TR/TE=3.3/1.54ms, FA=37°, BW=822Hz/px, 34-channel reception.
ii) 2D brain imaging at R=6×: FOV=240×240mm2, mtx=160×160, 4.5mm slice, TR/TE=3.37/1.57ms, FA=47°, BW=845Hz/px, 32-channel reception.
iii) SMS brain imaging at MB-8: Eight slices were acquired using parameters from case ii). To simulate SMS acquisition, these slices were shifted by multiples of FOV/4 and collapsed retrospectively. Since alternating the RF phase leads to a shift in both FOV and frequency [5], a collapsed slice group has contribution from all phase-cycles. As such, slices from appropriate cycles were shifted and collapsed.
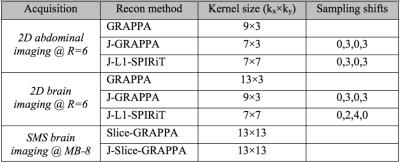
GRAPPA, Joint-GRAPPA and Joint L1-SPIRiT were employed for reconstruction of the 2D acquisition cases, while Slice- and Joint Slice-GRAPPA, both with leak-block [10], were used to reconstruct the SMS data. All experiments used 32 ACS lines, 12 GCC compressed channels [7] and 300 Monte-Carlo iterations for g-factor calculation [8]. Kernel sizes, under-sampling pattern staggering between phase-cycles, and regularization parameters were selected for optimal RMSE in each case (parameters in Fig4).
Results
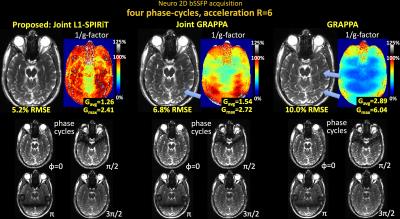
Fig1 shows reconstructed MIP images, error and g-factor maps for 2D abdominal imaging at R=6×. With GRAPPA, significant image artifacts are observed (blue arrows) along with a marked reduction in SNR, as reflected by the high g-factor. The image reconstruction improves with Joint-GRAPPA, and improve further still with Joint L1-SPIRiT to provide high quality reconstruction at ~2× lower RMSE and g-factor penalty.
Fig2 shows results for 2D brain imaging at R=6×, where Joint L1-SPIRiT also provides a similar reconstruction quality boost.
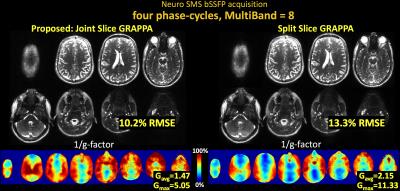
Fig3 shows results for SMS brain imaging at MB-8, where joint reconstruction via Joint Slice-GRAPPA provides 1.3× reduction in RMSE and 1.5× reduction in g-factor.
Discussion
Joint L1-SPIRiT employed banding artifacts as additional spatial encoding along with TV regularization. This provided up to 2-fold reduction in RMSE and noise amplification for highly accelerated phase-cycled 2D and SMS bSSFP acquisitions. Such reconstruction approach should enable rapid imaging of banding-free, high-SNR bSSFP images.
Acknowledgements
NIH grant numbers R01EB020613, R24MH106096, R01EB019437, P41EB015896 and R01EB017337.References
1. Griswold M, Jakob P, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn. Reson. Imaging 2002;47.6:1202–1210. doi: 10.1002/mrm.10171.
2. Lustig M, Pauly J. SPIRiT: Iterative self consistent parallel imaging reconstruction from arbitrary k space. Magn. Reson. Med. 2010;64.2:457–471. doi: 10.1002/mrm.22428.
3. Larkman D, Hajnal J, Herlihy AH, Coutts GA, Young IR, Ehnholm G. Use of multicoil arrays for separation of signal from multiple slices simultaneously excited. J. Magn. Reson. Imaging 2001;13:313–317.
4. Stäb D, Ritter C, Breuer F, Weng AM, Hahn D, Köstler H. CAIPIRINHA accelerated SSFP imaging. Magn. Reson. Med. 2011;65:157–164. doi: 10.1002/mrm.22600.
5. Wang Y, Shao X, Martin T, Moeller S, Yacoub E, Wang DJJ. Phase-cycled simultaneous multislice balanced SSFP imaging with CAIPIRINHA for efficient banding reduction. Magn. Reson. Med. 2015. doi: 10.1002/mrm.26076.
6. Bilgic B, Witzel T, Bhat H, Wald L, Setsompop K. Joint Reconstruction for Phase-Cycled Balanced SSFP. In: NYU i2i Workshop. ; 2016.
7. Huang F, Akao J, Vijayakumar S, Duensing GR, Limkeman M. k-t GRAPPA: A k-space implementation for dynamic MRI with high reduction factor. Magn. Reson. Med. 2005;54:1172–1184. doi: 10.1002/mrm.20641.
8. Dai E, Ma X, Zhang Z, Yuan C, Guo H. Simultaneous multislice accelerated interleaved EPI DWI using generalized blipped-CAIPI acquisition and 3D K-space reconstruction. Magn. Reson. Med. 2016. doi: 10.1002/mrm.26249.
9. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182–95. doi: 10.1002/mrm.21391.
10. Cauley SF, Polimeni JR, Bhat H, Wald LL, Setsompop K. Interslice leakage artifact reduction technique for simultaneous multislice acquisitions. Magn. Reson. Med. 2014;72:93–102. doi: 10.1002/mrm.24898.
11. Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 2013;69:571–582. doi: 10.1002/mrm.24267.
12. Breuer FA, Kannengiesser SAR, Blaimer M, Seiberlich N, Jakob PM, Griswold MA. General formulation for quantitative G-factor calculation in GRAPPA reconstructions. Magn. Reson. Med. 2009;62:739–746. doi: 10.1002/mrm.22066.
Figures
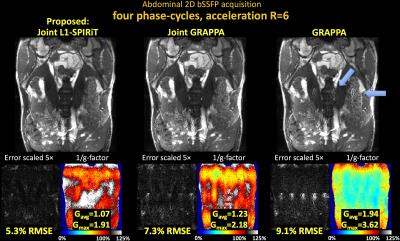
Fig1. Single slice bSSFP acquisition in the abdomen at R=6 fold acceleration. MIP images are displayed over 4 phase-cycles. Joint L1-SPIRiT reconstructs the phase-cycles jointly to leverage the B0 artifacts in the cycles as additional spatial encoding. This allows 72% reduction in RMSE and 1.8-fold reduction in average g-factor relative to GRAPPA. Such SNR improvement is similar to three averages of GRAPPA reconstruction. Blue arrows point to artifacts in the GRAPPA image, which have been mitigated by joint reconstruction.