Synopsis

At ultra-high field, transmit RF field inhomogeneity mitigation methods exploiting parallel transmission and multi-spoke pulses are readily applicable for brain imaging with small flip angle (FA) protocols. The extension to large FAs yet appears more challenging due to the inherent computationally extensive calculations. Dealing now with multi-slice applications, where specific absorption rate (SAR) issues often come into play, a SAR-aware slice-specific pulse design algorithm can improve significantly the output. This work thus presents a large FA slice-specific multi-spoke pulse design approach enforcing explicitely SAR constraints and, to reduce computations, where the spin dynamics is approximated with Average Hamiltonian Theory.

Introduction

At ultra-high field, transmit RF field inhomogeneity mitigation methods exploiting parallel transmission (pTx) and multi-spoke pulses are becoming mature for in vivo brain imaging but to date only in the small flip angle (FA) regime^1-4. To handle large FAs, pure numerical approaches consisting of discretizing RF envelopes into piecewise constant intervals⁵ can be used but, doing so, the computational complexity is increased dramatically. Additionally, when dealing with large FA multi-slice 2D-sequences, the user is often confronted to specific absorption rate (SAR) issues. Here, a SAR-aware slice-specific pulse design can provide a quasi-optimal solution provided that the spokes parameters (RF coefficients and spoke locations) of all slices are optimized within a single SAR-constrained optimization problem⁶. The latter, may be written as:

$$\mathbf{JP}:\min_{\left\{{p}_j\right\}}\sum_{j=1}^{M}\left\|\mathbf{A}_j(\mathbf{p}_j)/\alpha_t-1\right\|_2^2$$

Method

For a constant RF envelope $$$s(t)$$$ (hard pulse) of duration $$$T$$$, the action of the RF pulse at a static field offset $$${\Delta}\!B_0$$$ is described by the rotation matrix $$$R$$$ of angle $$$\theta={\gamma}{T}\sqrt{\left|s(T/2)B_1^+\right|^2+{\Delta}\!B_0^2}$$$ and rotation axis $$$\left[\text{Re}(s(T/2)B_1^+),\text{Im}(s(T/2)B_1^+),{\Delta}\!B_0\right]/\sqrt{\left|s(T/2)B_1^+\right|^2+{\Delta}\!B_0^2}$$$. For a time-varying envelope, the first order AHT approximates $$$R$$$ as $$$e^{-i\gamma{\Delta}\!B_0\sigma_z{T}/4}e^{-i(A^{(0)}+A^{(1)})}e^{-i\gamma{\Delta}\!B_0\sigma_z{T}/4}$$$ where, for a time-symmetric RF envelope, the terms $$$A^{(0,1)}$$$ take the form:

$$A^{(0)}=\frac{\gamma}{2}\left(\sigma_x\text{Re}(s(T/2)B_1^+)+\sigma_y\text{Im}(s(T/2)B_1^+)\right)\times\int_{-T/2}^{T/2}s_0(t+T/2)\cos(\gamma\Delta\!B_0{t})dt,$$

and:

$$ A^{(1)}=\frac{\gamma^2}{4}\sigma_z\left|s(T/2)B_1^+\right|^2\times\int_{0}^{+\infty}g(t)\sin(\gamma \Delta\!B_0{t})dt,$$

where $$$B_1^+$$$ denotes the complex transmit sensitivity, $$$\sigma_{x,y,z}$$$ are the Pauli matrices, $$$s_0(t)=s(t)/s(T/2)$$$ and $$$g(t)=\int_0^T{s_0}(t+u)s_0^{\star}(u)du$$$. Approximating $$$\mathbf{A}_j(\mathbf{p}_j)$$$ by using AHT thus reduces considerably the complexity compared to a numerical Bloch integration because no discretization of $$$s(t)$$$ is required.

To solve JP under constraints, the following procedure was used: 1) Choose randomly $$$N_{\text{seed}}$$$ k-space trajectory seeds⁹, 2) For each trajectory seed and for each slice separately, solve the slice-specific problem using the active-set algorithm (A-S) while multiplying the RF pulse duty-cycle by $$$M$$$ for evaluating the constraints ($$$M\times N_{\text{seed}}$$$ independent optimizations), 3) Select for each slice the best solution out of the $$$N_{\text{seed}}$$$ trials and “merge” the solutions (slice-by-slice design), 4) Starting from this feasible but likely suboptimal solution, solve JP using A-S.

The proposed pulse design approach was applied to the Siemens 2D interleaved multi-slice GRE sequence (0.5×0.5 mm² voxels, 25 slices, 2 mm slice thickness, 3 mm slice gap, TR=2 s, bandwidth=50 Hz/pixel, TE=16 ms, nominal FA=90°, GRAPPA 2, TA~8 min). That protocol was first applied in the usual circularly polarized (CP) transmission mode and subsequently with optimized 3-spoke RF pulses. Here the optimization of the pulses was based upon patient specific field maps which were measured beforehand¹⁰.

Results

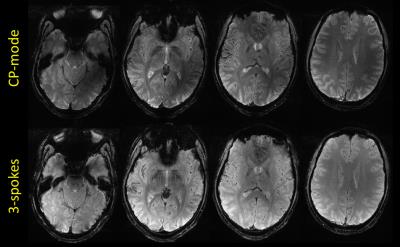
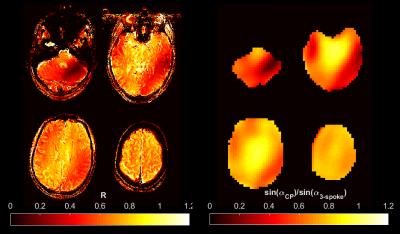
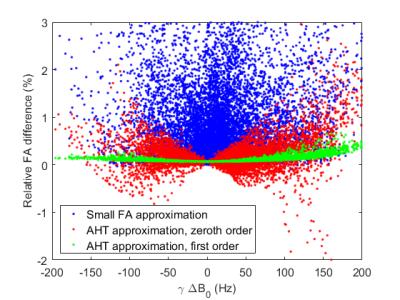
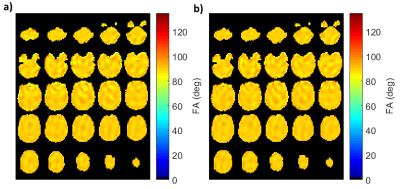
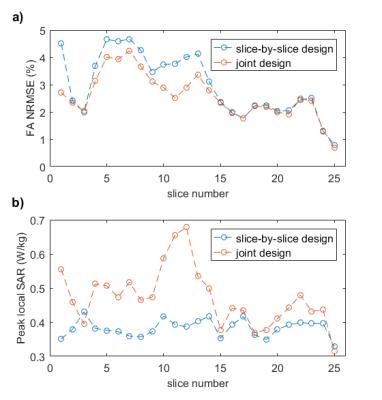
A comparison of the CP- and 3-spoke-GRE images is provided in Figure 1. The relative signal-to-noise ratio (SNR) comparison obtained by computing the ratio R of both images, is shown in Figure 2 together with a simulation of $$$\sin(\alpha_{\text{CP}})/\sin(\alpha_{\text{3-spoke}})$$$, $$$\alpha_{\text{CP}}$$$ and $$$\alpha_{\text{3-spoke}}$$$ denoting the simulated FA profile of the CP and 3-spoke pulses. Despite the presence of incomplete T₁ which can bias the comparison by up to 20%, both images reveal qualitatively similar patterns. The FA simulations of the optimized 3-spoke pulses by numerical Bloch integration indicate that the overall FA normalized root mean square error (NRMSE) is below 3%, while none of the 25 slices exceeds 5% NRMSE. With the proposed method, the computation time required to obtain the 25 pulses was 542 s on a Xeon E5-2690 bi-processor and could be decreased down to 228 s by porting the AHT calculation on a K40 Nvidia (Santa Clara, CA, USA) GPU card. The precision of the first and second order AHT, reported in Figure 3, indicate that the first order AHT is perfectly adequate for the purpose of designing multi-spoke pulses. Figure 4 compares in simulation the FA profiles obtained with the slice-by-slice approach and the joint design approach. Figure 5 reports, slice-wise, the respective NRMSE and local SAR distributions and describes how performances can be increased with the proposed joint design.

Conclusion

This work demonstrates that the B1 inhomogeneity problem can be mitigated efficiently in a multi-slice near whole-brain coverage UHF protocol involving large FA pulses using a rapid pulse design active-set based algorithm exploiting AHT.

Acknowledgements

References