0386

Faster than Mulitband ... Advanced Pseudo Fourier Imaging's (API) response to the current state of the art

Nishant Zachariah¹, Jason Langley², Justin Romberg¹, and Xiaoping P. Hu³

¹Department of Electrical and Computer Engineering, Georgia Institute of Technology, Atlanta, GA, United States, ²Center for Advanced Neuroimaging, University of California at Riverside, CA, United States, ³Department of Bioengineering, University of California at Riverside, CA, United States

Synopsis

Multiband (MB) imaging is limited in its acceleration factor by the high correlation that exists between receiver coils. In this work, we present a novel technique, Advanced Pseudo Fourier Imaging (API) which achieves parallel excitation beyond that which is currently possible using multiband imaging. In doing so, API forms a generic framework for seamless transition from 2D to 3D imaging. Unlike MB, API is less sensitive to the RF excitation profile in its slice reconstruction by virtue of the introduced phase variations. We demonstrate the viability of API through 1D simulations and 3D head phantom data acquired at 3T.

Introduction

Current multiband (MB) techniques are fundamentally limited in their ability to separate a large number of simultaneously acquired slices[1-3]. These highly correlated coil sensitivity profiles generate an ill posed reconstruction. Existing methods such as CAIPIRINHA[2] and Blipped CAIPI[1] uses static FOV shifts in plane to improve the slice separation. Furthermore, the slice profiles of images reconstructed with MB are dictated by excitation pulses. To alleviate these challenges, we extend Pseudo Fourier imaging[4] to the multi-coil case and redesign its reconstruction process. The resultant technique (Advanced Pseudo Fourier Imaging: API) forms a generalized imaging framework for seamless transition between 2D – 3D imaging. API frees slice reconstruction from a crippling dependency on the RF excitation profile and is able to achieve higher acceleration factors relative to MB.

Methods

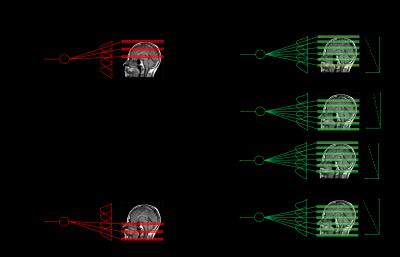
1D Simulation: The multiband (MB) model (in 1D) can be expressed as$$y_{k,i} = \int_z w_k(z) c_i(z) f(z) dz + n \;\; ... (\text{Eq. 1}) $$where $$$y_{k,i}$$$ is the MB signal observed at the $$$k$$$th excitation through the $$$i$$$th coil, $$$w_k(z)$$$ is the $$$k$$$th excitation window, $$$c_i(z)$$$ represents the coil sensitivity profile of the $$$i$$$th coil, $$$f(z)$$$ is the unknown signal that needs to be recovered and $$$n$$$ is the unknown noise. API introduces a continually varying phase and can be written as $$b_{k,i} = \int_z \bar{w}_k(z) c_i(z) f(z)e^{-j\omega_k z} dz + n \;\; ... (\text{Eq. 2})$$where $$$b_{k,i}$$$ is the API signal observed at the $$$k$$$th excitation through the $$$i$$$th coil, $$$\bar{w}_k(z)$$$ denotes the multi-slice $$$k$$$th excitation API window and $$$\omega_k$$$ the applied phase encode gradient (Fig 1). Excitation windows were modeled as a conglomeration of apodized sinc functions and the coil profiles were generated using Biot-Savart’s law. To demonstrate API’s insensitivity towards excitation profile (unlike MB), the API excitation windows were larger than their MB counterparts with 50% overlap between successive excitations (Fig 2-4).

3D Data Acquisition: Data from a head phantom were acquired on a Siemens 3T Prisma Fit (Malvern, PA) using a GRE with a flip angle of 30$$$^\circ$$$, pixel bandwidth of 30Hz, TE of 18.5msec, TR of 38msec, FOV of 158x390198 mm and resolution of 1x1x2mm. The coil profiles were estimated using a pre-scan. Phase gradient and multi-slice excitation was implemented retrospectively for ground truth comparisons with the final reconstruction.

Tikhonov regularized least squares was used to recover in Eq1&2. Reconstruction accuracy was quantified using normalized recovery error and peak signal to noise ratio across a range of noise profiles.

Results

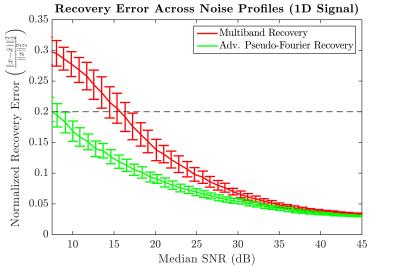
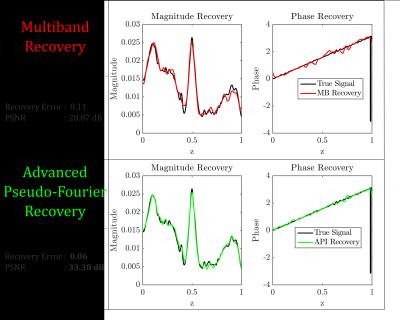
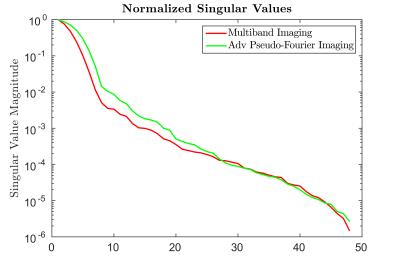
1D Simulation: As an initial proof of concept, the methodology was tested for an analytic 1D case across a range of noise profiles (Fig 2). At an acceleration factor of 8, API consistently recovered the underlying signal with greater fidelity by nearly $$$40-50\%$$$ at the higher noise levels relative to multiband imaging (Fig 2). For the noise matched case, API recovers the underlying signal with $$$50\%$$$ less error than multiband (Fig 3). This increase in robustness can be attributed to the spectral spread of the API encoding operator relative to MB (Fig 4). As seen in Fig 3, despite API utilizing an excitation window that is twice as large as MB with 50% overlap, API reconstructs the underlying signal with significantly lower error.

3D Simulation: At an acceleration factor of 8 (which causes MB to fail on our scanner), we find that API recovers the underlying signal with $$$50\%$$$ less recovery error and approximately $$$6$$$dB increase in reconstruction accuracy (Fig 5). Residuals for MB are significantly higher than that for API. Examples of specific slice reconstructions for the head phantom are shown in Fig 5.

Discussion and Conclusion

Our results show that API allows for achieving acceleration factors at which existing multiband recovery fails. At acceleration factors for which MB works, API provides improved robustness in the presence of noise. The applied phase differential de-correlates the high correlated coil profiles ensuring that API has a larger reachable subspace relative to MB (Fig 4). In all simulations multiband was afforded the same regularized recovery process as API to ensure a fair comparison. Furthermore, since the published implementation of multiband does not utilize our regularized reconstruction framework (which ensures higher signal reconstruction fidelity), in practice the gap between API and standard MB will be much larger. The formulation used for API forms a generalized framework for 2D–3D imaging on a continuous spectrum. API benefits greatly from its slice reconstruction being less dependent on the utilized excitation profile (unlike MB). API can be extended in the future by incorporating existing in-plane acceleration techniques such as GRAPPA[5], SENSE[6] and compressed sensing[7-8].

Acknowledgements

The authors would like to thank the members of the Biomedical Imaging and Technology Center at Georgia Tech and Emory University for scanner time.

References

[1] Setsompop, Kawin, et al. "Blipped-controlled aliasing in parallel imaging for simultaneous multislice echo planar imaging with reduced g-factor penalty." Magnetic Resonance in Medicine 67.5 (2012): 1210-1224.

[2] Breuer, Felix A., et al. "Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging." Magnetic resonance in medicine 53.3 (2005): 684-691.

[3] Moeller, Steen, et al. "Multiband multislice GE-EPI at 7 tesla, with 16-fold acceleration using partial parallel imaging with application to high spatial and temporal whole-brain fMRI." Magnetic Resonance in Medicine 63.5 (2010): 1144-1153.

[4] Kadah, Yasser M., and Xiaoping Hu. "Pseudo-Fourier imaging (PFI): A technique for spatial encoding in MRI." IEEE transactions on medical imaging 16.6 (1997): 893-902.

[5] Griswold, Mark A., et al. "Generalized autocalibrating partially parallel acquisitions (GRAPPA)." Magnetic resonance in medicine 47.6 (2002): 1202-1210.

[6] Pruessmann, Klaas P., et al. "SENSE: sensitivity encoding for fast MRI." Magnetic resonance in medicine 42.5 (1999): 952-962.

[7] Candes, Emmanuel J., Justin K. Romberg, and Terence Tao. "Stable signal recovery from incomplete and inaccurate measurements." Communications on pure and applied mathematics 59.8 (2006): 1207-1223.

[8] Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic resonance in medicine 58.6 (2007): 1182-1195.

Figures

Fig 1. Schematic of multiband (MB) Imaging (left) and Advanced Pseudo-Fourier Imaging (API). For the MB example shown, 3 slices are simultaneously excited and are seen through a receiver array of coils for a total of K acquisitions. In API, twice the number of slices are excited at a given time (6 slices in this example) but a phase encode gradient is applied at each acquisition. Thus while the number of acquisitions stays identical at K, each location is seen more than once.

Fig 2. Summary of signal recovery error for multiband (MB) and advanced pseudo Fourier imaging (API) along the slice direction for a range of noise profiles. The plotted result demonstrates that not only is API more robust than MB but it is capable of acceleration in noise regimes where MB would not be feasible. In the practical noise regime (standard MR noise regime 10-25 dB), API can outperform MB by as much as 50%. It is interesting to note that API consistently recovers signals with less error than 0.2 (black broken line) across all tested noise profiles unlike MB.

Fig 3. Exemplar signal recovery for Multiband (MB) and Advanced Pseudo Fourier Imaging (API) for an identical instantiation of noise (23.51 dB). API recovers the underlying signal with ~50% less error than MB. If the magnitude image is considered, the peak signal to noise ratio (reconstruction accuracy) of API is ~5dB higher than that of MB imaging. In addition, a cursory examination of the plots will reveal that API (green) is even visually closer to the underlying signal (black) than MB imaging (red).

Fig 4. Normalized spectral distribution of the multiband (MB) encoding operator and the advanced pseudo-Fourier imaging (API) encoding operator. From the plot, it becomes clear that API (red) has a higher area under the curve which engenders API with robust recovery relative to MB imaging. Also, API is better conditioned but it must be noted that the last few singular values are not utilized in the reconstruction by virtue of the Tikhonov regularization used for both MB and API.

Fig 5. Recovery exemplars for 3D head phantom using multiband (MB) and advanced pseudo Fourier imaging (API) for an acceleration factor of 8 (SNR of 35dB). A cursory examination of the residuals (factor 5 magnified for viewing) demonstrate that MB recovers the underlying signal with large errors. This is also seen in the raw reconstructed images where the g-factor penalty is beginning to show. Both the raw API reconstructed images and the residuals are devoid of the errors seen in the MB case. The recovery error quantified in the bar graph . API recovers the underlying signal with 50% lower error.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0386