Synopsis

We present a method to minimize signal intensity variations observed when performing balanced steady state free precession imaging in non-uniform B₀ and B₁+ fields. This is achieved by harnessing parallel transmission, with RF shims calculated in order to produce the most uniform signal for the desired tissues given measured B₀ and B₁+ field maps.

Purpose

Balanced Steady-State Free Precession (bSSFP)$$$^1$$$ offers ultra-high resolution structural$$$^{2,3}$$$ and functional$$$^4$$$ imaging at ultra-high field (UHF), but is impaired by $$$B_0$$$-inhomogeneity, transmit field ($$$B_1^+$$$)-inhomogeneity and power deposition. These effects result in SAR-limited UHF-bSSFP acquisitions that produce images with uneven signal/contrast.

Many methods have been developed to mitigate the effects of $$$B_0$$$-inhomogeneity on bSSFP$$$^{5-9}$$$, and bSSFP can incorporate parallel transmission (PTx) $$$B_1^+$$$-inhomogeneity correction strategies$$$^{3,10}$$$. Here we propose a novel approach to mitigate $$$B_0$$$ and $$$B_1^+$$$-inhomogeneity for bSSFP in a single unified manner. We apply Direct Signal Control$$$^{11,12}$$$ to bSSFP for the first time, harnessing PTx to improve image uniformity in spite of field inhomogeneities.

Methods

The bSSFP steady-state magnetization at TE=TR/2 with flip angle $$$\alpha$$$ and 0-180° phase cycling with relaxation times $$$T_1$$$ and $$$T_2$$$ and off-resonance $$$d\omega$$$ is given below ($$$\mathbf{R}_\beta$$$=rotation matrix of angle $$$\beta$$$, $$$\mathbf{P}_t$$$=precession/$$$T_2$$$-decay matrix for duration $$$t$$$, $$$\mathbf{b}$$$=$$$T_1$$$-recovery vector)$$$^{13}$$$.

$$\mathbf{M}(TR,\alpha,d\omega,T_1,T_2)=\mathbf{P}_{TR/2}[\mathbf{I}-\mathbf{R}_{\alpha}\mathbf{P}_{TR}\mathbf{R}_{-\alpha}\mathbf{P}_{TR}]^{-1}[\mathbf{R}_{\alpha}\mathbf{P}_{TR}\mathbf{R}_{-\alpha}\mathbf{b}+\mathbf{R}_{\alpha}\mathbf{b}]$$

$$$B_0$$$/$$$B_1^+$$$ inhomogeneity results in spatially variable fields (i.e. $$$\alpha=\alpha_j$$$, $$$d\omega=d\omega_j$$$; $$$j$$$=voxel index), causing spatially variable signal $$$f(TR,\alpha_j,d\omega_j,T_1,T_2)=\sqrt{M_x^2+M_y^2}$$$. We propose exploiting additional freedom offered by multiple ($$$N_{tx}$$$) transmitters to achieve signal uniformity by solving the optimization problem below ($$$\Phi$$$=cost function to be minimized, $$$\mathbf{w}$$$=$$$N_{tx}$$$x1 complex vector of RF shims, $$$\alpha_j^k$$$=flip angle profile of transmitter $$$k$$$, $$$i$$$=1,…,$$$N_{tiss}$$$ is an index of included tissues, $$$d_i$$$=desired signal, $$$P_{lim}$$$=RF power limit used as a surrogate for SAR).

$$\newcommand{\abs}[1]{\left|#1\right|}\underset{\bf{w}}{\text{minimize}}\enspace\Phi=\sum_{i=1}^{N_{tiss}}\sum_{j=1}^{N_{vox}}\abs{d_i-f\left(TR,\sum_{k=1}^{N_{tx}}\alpha^k_jw^k,d\omega_j,T_1^i,T_2^i\right)}^2\enspace\text{subject}\;\text{to}\enspace\mathbf{w}^*\mathbf{w}\leq\text{P}_{lim}$$

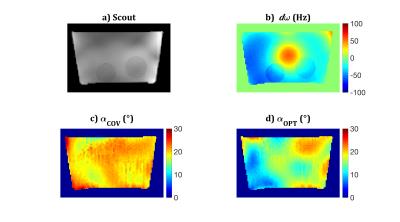
This approach was tested experimentally. Measurements were performed on a Siemens Magnetom-7T with an eight-channel transmit/receive head coil (Rapid Biomedical). A phantom was constructed containing Magnevist-doped saline ($$$T_1$$$=1236ms, $$$T_2$$$=611ms) with two chambers of 0%-fat milk ($$$T_1$$$=1949ms, $$$T_2$$$=91ms) and a spherical air cavity (diameter=40mm) to induce $$$B_0$$$-inhomogeneity. Images were acquired in a single transverse slice with FOV=200x112.5mm, located 30mm superior to the cavity. Flip angle profiles were obtained by relative $$$B_1^+$$$ mapping$$$^{14,15}$$$ and multi-angle absolute $$$B_1^+$$$ mapping$$$^{16}$$$. $$$B_0$$$ shimming utilized a manufacturer-provided protocol (WIP-452G). The center frequency was set to minimize the maximum $$$|d\omega_j|$$$. $$$B_0$$$ mapping was performed with a multi-echo SPGR (TEs=2,4,…,10ms).

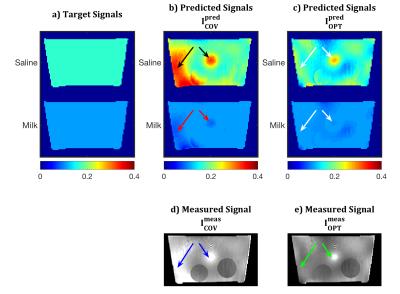
Two RF shims were used for bSSFP acquisitions (vox=2x2x1mm, TR=6.7ms, BW=685Hz/pix). The first, $$$\mathbf{w}_{COV}$$$, producing flip angle map $$$\alpha_{COV}$$$, was obtained from a Coefficient-of-Variation (COV) optimisation$$$^{17}$$$, and scaled to achieved an average $$$\alpha$$$=20° (chosen to meet transmitter RF power limits). The second, $$$\mathbf{w}_{OPT}$$$, producing flip angle map $$$\alpha_{OPT}$$$, was obtained from the proposed method. All field information was passed to the routine for calculation, target signals $$$d_i$$$ were set as the signals obtained on-resonance with $$$\alpha$$$=20° (i.e. $$$f(TR,20^\circ,0,T_1^i,T_2^i)$$$), and $$$P_{lim}$$$=$$$\mathbf{w}_{COV}^*\mathbf{w}_{COV}$$$. An initial search was performed using 100,00 random RF shims; the 20 best were used for initialisation of the Matlab routine fmincon. $$$\mathbf{w}_{OPT}$$$ was chosen as the best solution. The bSSFP acquisitions were corrected for receiver bias to produce $$$I_{COV}^{meas}$$$ and $$$I_{OPT}^{meas}$$$, which were compared to the predicted images for each substance and method, $$$I_{COV,i}^{pred}$$$ and $$$I_{OPT,i}^{pred}$$$.

Results

The $$$B_0$$$ map (Fig.1b) shows a central perturbation (+55Hz) due to the air cavity. The minimum frequency is -65Hz; note the localized ~10Hz artifact due to the chemical shift of milk. $$$\alpha_{COV}$$$ is more uniform than $$$\alpha_{OPT}$$$ (Figs.1c/d; standard deviations of 1.9° and 3.8° respectively). Whilst in conventional sequences $$$\alpha_{COV}$$$ would produce a more uniform image than $$$\alpha_{OPT}$$$, Fig.2 demonstrates that the converse is true for bSSFP in this scenario.

$$$I_{COV}^{pred}$$$ (Fig.2b) has signal hyper/hypo-intensities (black/red arrows) in regions of large $$$B_0$$$-inhomogeneities. These also appear in $$$I_{COV}^{meas}$$$ (Fig.2d, blue arrows). $$$I_{OPT}^{pred}$$$ shows reduced signal inhomogeneity (Fig.2c, white arrows), which is confirmed by experiment ($$$I_{OPT}^{meas}$$$, Fig.2e, green arrows).

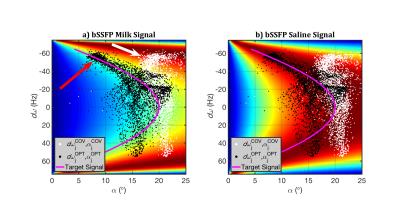
Figure 3 gives further insight. Each image shows the predicted bSSFP signal as a function of $$$d\omega$$$ and $$$\alpha$$$ (Fig.3a, milk; Fig.3b, saline). The desired signal $$$d_i$$$ is indicated in magenta; note that lower $$$\alpha$$$ is required to obtain $$$d_i$$$ when $$$d\omega$$$≠0. Each overlaid scatter-point corresponds to a voxel (white, $$$I_{COV}^{pred}$$$; black, $$$I_{OPT}^{pred}$$$), placed according to its $$$d\omega_j$$$ and corresponding $$$\alpha_j$$$. Signals from $$$I_{COV}^{pred}$$$ exhibit less variation along the $$$\alpha$$$-axis as $$$\alpha_{COV}$$$ is uniform, but off-resonance distributes the points along the $$$d\omega_j$$$-axis, resulting in non-uniform signal (white arrow). However, our proposed technique alters $$$\alpha_{OPT}$$$ so that signals from $$$I_{OPT}^{pred}$$$ are closer to the desired signal (red arrow).

Finally, the power ratio $$$\mathbf{w}_{OPT}^*\mathbf{w}_{OPT}$$$/$$$\mathbf{w}_{COV}^*\mathbf{w}_{COV}$$$=0.52; whilst this implies reduced SAR, further experiments are required to see if this is a reproducible feature of the proposed method.

Discussion and Conclusions

Acknowledgements

References

1. Miller, K. L., Hn Tijssen, R., Stikov, N. & Okell, T. W. Steady-state MRI: methods for neuroimaging. Imaging Med 3, 93–105 (2011).

2. Zeineh, M. M. et al. Ultrahigh-resolution imaging of the human brain with phase-cycled balanced steady-state free precession at 7 T. Invest. Radiol. 49, 278–89 (2014).

3. Hahnemann, M. L. et al. Non-enhanced magnetic resonance imaging of the small bowel at 7 Tesla in comparison to 1.5 Tesla: First steps towards clinical application. Magn. Reson. Imaging 34, 668–673 (2016).

4. Scheffler, K. & Ehses, P. High-resolution mapping of neuronal activation with balanced SSFP at 9.4 tesla. Magn. Reson. Med. 0, n/a--n/a (2015).

5. Lee, J., Lustig, M., Kim, D. & Pauly, J. M. Improved shim method based on the minimization of the maximum off-resonance frequency for balanced steady-state free precession (bSSFP). Magn. Reson. Med. 61, 1500–1506 (2009).

6. Zur, Y., Wood, M. L. & Neuringer, L. J. Motion-Insensitive, Steady-State Free Precession Imaging. Magn. Reson. Med. 16, 444–459 (1990).

7. Leupold, J., Hennig, J. & Scheffler, K. Alternating repetition time balanced steady state free precession. Magn. Reson. Med. 55, 557–565 (2006).

8. Nayak, K. S., Lee, H. L., Hargreaves, B. A. & Hu, B. S. Wideband SSFP: Alternating repetition time balanced steady state free precession with increased band spacing. Magn. Reson. Med. 58, 931–938 (2007).

9. Nielsen, J. F., Yoon, D. & Noll, D. C. Small-tip fast recovery imaging using non-slice-selective tailored tip-up pulses and radiofrequency-spoiling. Magn. Reson. Med. 69, 657–666 (2013).

10. Padormo, F., Beqiri, A., Hajnal, J. V. & Malik, S. J. Parallel transmission for ultrahigh-field imaging. NMR Biomed. 29, 1145–1161 (2016).

11. Malik, S. J., Padormo, F., Price, A. N. & Hajnal, J. V. Spatially resolved extended phase graphs: Modeling and design of multipulse sequences with parallel transmission. Magn. Reson. Med. 68, 1481–1494 (2012).

12. Malik, S. J., Beqiri, A., Padormo, F. & Hajnal, J. V. Direct signal control of the steady-state response of 3D-FSE sequences. Magn. Reson. Med. 73, 951–963 (2015).

13. Lee, K. J., Lee, H. L., Hennig, J. & Leupold, J. Use of simulated annealing for the design of multiple repetition time balanced steady-state free precession imaging. Magn. Reson. Med. 68, 220–226 (2012).

14. Van De Moortele, P.-F. et al. Calibration Tools for RF Shim at Very High Field with Multiple Element RF Coils: from Ultra Fast Local Relative Phase to Absolute Magnitude B1+ Mapping. in Proceedings of the ISMRM 1676 (2007).

15. Brunner, D. O. & Pruessmann, K. P. SVD analysis of Array transmission and reception and its use for bootstrapping calibration. Magn. Reson. Med. n/a-n/a (2016). doi:10.1002/mrm.26060

16. Klose, U. Mapping of the radio frequency magnetic field with a MR snapshot FLASH technique. Med. Phys. 19, 1099 (1992).

17. Mao, W., Smith, M. B. & Collins, C. M. Exploring the limits of RF shimming for high-field MRI of the human head. Magn. Reson. Med. 56, 918–922 (2006).

18. Çukur, T. & Nishimura, D. G. Multiple repetition time balanced steady-state free precession imaging. Magn. Reson. Med. 62, 193–204 (2009).