Synopsis

We have recently introduced cross-term SPatiotemporal ENcoding (xSPEN), a technique with exceptional resilience to field heterogeneities. Like other single-shot methods, however, xSPEN’s resolution and SNR are intrinsically limited. This study explores a multi-scan, phase-encoded extension of xSPEN, which improves sensitivity while increasing resolution along both the phase-encoded and the slice-selection dimensions simultaneously. This reflects xSPEN’s unusual kernel whereby a y-axis can be sampled by a z-gradient and viceversa. Furthermore, as each phase-encoded xSPEN scan provides an entire 2D image, each low-resolution xSPEN scan in the set may be used to correct motions leading to very high definition 3D MRI capabilities.

Purpose

Methods

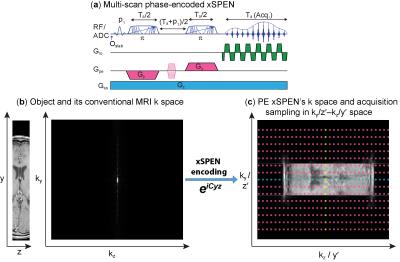
xSPEN is a single-shot imaging technique using frequency-swept pulses under the action of bipolar ±G_y and constant G_z gradients, to impart a hyperbolic phase e^iCyz modulation; assuming a uniform object across the slice thickness Δz, subsequent readout by k_z=γG_zt provides what we referred to as a low-resolution y′=k_z/C profile.¹ Resolution of this y-axis profile is given by the time-bandwidth product Q of the frequency-swept encoding pulses;¹ here we seek to improve this resolution by performing additional k_y encodings in independent scans (Fig. 1a).

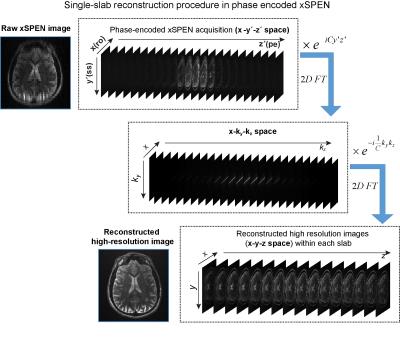
The bidimensional e^iCyz kernel encoding spins in xSPEN leads to a unique situation, whereby the k-space sampling is spread from the well-localized situation of traditional MRI (Fig. 1b) into a 2D box-like shape (Fig. 1c). Single-shot xSPEN¹ only captures the k_z /y′ axis for k_y=0 (Fig. 1c, blue dots); conversely, should one collect signals under the action of G_y (k_z=0), the outcome would be a k_y/z′ image (Fig. 1c, yellow dots). While this 2D kernel underlies xSPEN’s uniqueness, it is also the main source of SNR loss of these single-shot implementations. This study remedies this by introducing a k_y-encoding that captures extended regions in k-space (Fig. 1c, magenta dots), improving SNR by Fourier multiplexing and resolution along the y-axis by probing higher k_ymax values. Furthermore, by exploring the z′= k_y/C profile, these k_y-acquisitions lift the need to assume uniform slices, augmenting the z-axis resolution by a factor ≤Q. Taking into account that xSPEN’s EPI-like ±k_x oscillations also yield a third, readout domain,² suitable reconstruction of such data yields high in-plane resolution as well as ultrahigh though-plane resolution within the excited slab. To extract this information a suitable analysis of the data in its unusual k_z/y′-k_y/z′ space is needed. Figure 2 summarizes one of the reconstruction procedures that based on such analysis we developed for this phase-encoded version of xSPEN. Remarkable aspects of this new imaging approach are that (i) the k-space kernel provided by the hyperbolic phase allows sampling along k_y to break the stringent Δk_y=1/FOV_y criterion, (ii) that sampling along k_y can actually extend beyond k_ymax by Q/FOV_y, and (iii) that the single-shot 2D nature underlying the phase encoded approach allows identification and elimination of motional artifacts.

Results and Discussion

Experimental tests of the proposals in Figs. 1 and 2 were carried out on an ex-vivo rat brain (Agilent 7T) and on a human volunteer (Siemens 3T).

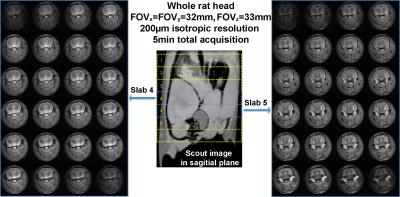
Figure 3 shows results collected at 200µm isotropic resolution for a whole rat brain in 5min. Each of the 7 excited slabs was 4.8mm and frequency swept pulses with Q=24 were used, leading to a 200µm slice-dimension resolution. With a Δk_y=1/FOV_y step and 136 k_y phase-encodes this led to k_ymax = 160/FOV_y, i.e. to a 200µm resolution across a FOV_y =32mm. Reconstructed z-slices from slabs 4 and 5 are shown in Fig. 3’s left and right panels. As almost all the energy associated to the object’s original k-space is captured and used by this experiment, its SNR is similar to a conventional Fourier imaging experiment with the same resolution.

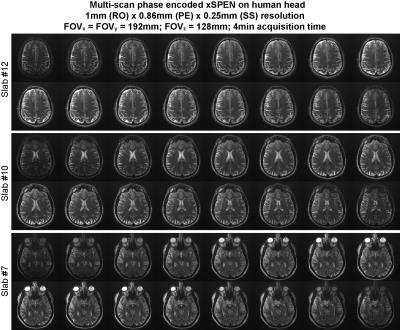
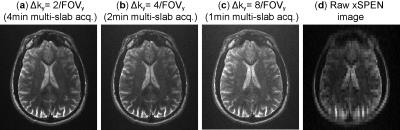
Figure 4 illustrates a 4min phase-encoded xSPEN acquisition on a human volunteer. A Δk_y=2/FOV_y step –twice as large as needed for normally encoding a FOV_y=192mm– was used, and the number of k_y phase-encodes was 96. When considering frequency swept pulses with Q=32 this spreads k_ymax to 224/FOV_y; after reconstruction this lead to a resolution Δy=0.85mm. Given the 8mm slabs and the Q=32 value used the reconstructed resolution along z was 0.25mm; however, the non-dense sampling along k_y also means that there will be a gap of 0.25 mm between the resolved z-slices. This loss of information is not here visible owing to the final thinness and denseness of the z-slices. In fact, Figure 5 illustrates how acquisition times can be shorten even further by undersampling along the phase encoding dimension with steps Δk_y= 4/FOV_y, 8/FOV_y, at no expense in the in-plane resolution (despite SNR degradation owing to the fewer scans). Only center slices from slab 10 are shown in Fig. 5.

Conclusions

Acknowledgements

References