Synopsis

Balanced steady-state free precession (bSSFP) cardiac MRI benefits greatly from reduced repetition time (TR). Minimum TR is often limited by specific absorption rate (SAR) and hardware constraints. RF shimming can be used with parallel transmission (PTx) to work within such constraints, but direct minimization of TR is not straightforward since the constraints themselves vary as TR is reduced.

We present an extended RF shimming framework in which PTx degrees of freedom are simultaneously optimised with pulse sequence properties. The result is minimum TR bSSFP sequences that operate at the SAR limits and within hardware constraints for 3T cardiac MRI.

Purpose

Theory

For a PTx system with $$$N_c$$$ channels, RF shimming is the process of determining an optimal set of complex dimensionless weighting $$$\mathbf{w}_j (j=1:N_c)$$$ to apply to each channel.

For a sequence with a given TR and RF pulse shape $$$p(t)$$$ we may write the constraints on $$$\mathbf{w}$$$ as a function of pulse duration ($$$\tau$$$):

\[constraints_{\mathbf{w}}(\tau):\left\{\begin{array}{ll}\max\limits_{i}\left\lbrace\mathbf{w^*Q_iw}\right\rbrace\times LF^2\times\dfrac{\theta_0^2}{\gamma^2}\times\dfrac{\delta_2}{\delta_1^2} \times\dfrac{1}{\tau TR}\leq lSAR_{max}\\\left\lbrace\mathbf{w^*Q_{wb}w}\right\rbrace\times LF^2\times\dfrac{\theta_0^2}{\gamma^2}\times\dfrac{\delta_2}{\delta_1^2} \times\dfrac{1}{\tau TR}\leq wbSAR_{max}\\|\mathbf{w}_j|\leq\tau\dfrac{P_{peak}}{\sqrt{A}} \dfrac{\delta_1\gamma}{\theta_0}\quad\forall j\\|\mathbf{w}_j|\leq\sqrt{\tau TR}\dfrac{\delta_1\gamma}{\theta_0\sqrt{\delta_2}}\sqrt{\dfrac{P_{avg}}{A}}\quad\forall j\end{array}\right.\]

Top-to-bottom these expressions represent local SAR (10g averaged), whole-body SAR, peak power and average power respectively.

$$$\mathbf{Q_{wb}}$$$ and $$$\mathbf{Q_{i}}$$$ are the whole body and local SAR matrices^4,5 and $$$\theta_0$$$ the target flip angle. $$$\delta_1$$$ and $$$\delta_2$$$ are intrinsic properties of $$$p(t)$$$ relative to a block pulse with the same flip angle and amplitude ($$$\delta_1$$$ is the relative duration, $$$\delta_2$$$ is the relative energy). $$$lSARmax$$$ and $$$wbSARmax$$$ are the local and whole-body SAR limits; $$$P_{peak}$$$ and $$$P_{avg}$$$ are peak and average RF power limits. $$$LF$$$ is a scalar ‘loading factor’ to match the SAR model and $$$A$$$ is a scalar that quantifies RF chain efficiency in W/$$$\mu$$$T².

The minimum TR is set by:

\[TR_{min} = max\left\{\begin{array}{ll}\tau+t_{enc}\\\tau/\delta_0\end{array}\right\}\]

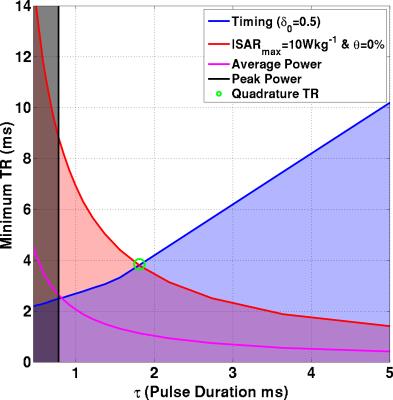
$$$t_{enc}$$$ is time required for image encoding and $$$\delta_0$$$ is the RF amplifier gating duty-cycle limit (50%). Figure 1 illustrates the intersection of these constraints for a single-channel system – the green circle indicates the TR that would be selected for scanning.

The optimization is performed using a nested approach with an outer step that seeks to find the lowest acceptable $$$\tau$$$ to minimize sequence TR:

$$\mathrm{arg\,min}_{\tau}\left\lbrace TR+f(\hat{\theta})\right\rbrace$$

where $$$f(\hat{\theta})$$$ is a function that penalises solutions with high bias $$$(\hat{\theta})$$$ in achieved flip angle within a region of interest (ROI). For each $$$\tau$$$, an inner optimization seeks optimal $$$\mathbf{w}$$$ given the constraints. This was done in two ways – one minimises mean squared error (MSE) in $$$\theta$$$:

$$\begin{align} \mathrm{arg\,min}&_{\mathbf{w}}\||\mathbf{S_{\theta}w}|-\mathbf{\theta_0}\|^2_{ROI}\\ \mathrm{s.t.}&\quad constraints_{\mathbf{w}}(\tau) \end{align}$$where $$$\mathbf{S_{\theta}}$$$ represents spatially dependent RF sensitivities of the transmit channels in units of achieved flip angle. Although MSE improves flip angle homogeneity in the target region, it cannot achieve a zero bias solution (5% bias was allowed). The second optimisation minimizes bias $$$\hat{\theta}$$$ alone:

$$\begin{align}\mathrm{arg\,min}&_{\mathbf{w}}\|\overline{|\mathbf{S_{\theta}w}|}-\theta_0\|^2_{ROI}\\ \mathrm{s.t.}&\quad constraints_{\mathbf{w}}(\tau)\end{align}$$

Methods

Experiments performed on a Philips 3T MRI system with an 8-channel transmit body array⁶ and 6-channel receiver array. Seven male subjects were scanned; each matched to one of two pre-calculated SAR models based on their body mass index (a smaller model (BMI=23.5) for subjects 1-5 and a larger model (BMI=31) for subjects 6&7).

B$$$_1^+$$$ mapping used DREAM⁷ and bSSFP imaging with $$$\theta_0$$$=45° was performed for a 4-chamber cardiac view. The ROI was manually drawn to only include myocardium. Optimal sequence parameters for the transmit coil quadrature mode (similar to a whole-body birdcage) were also determined using the outlined approach (Figure 1).

Results

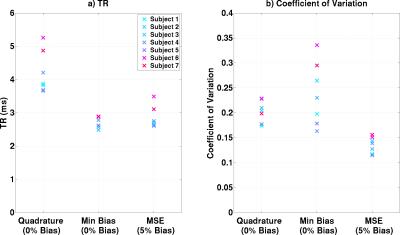
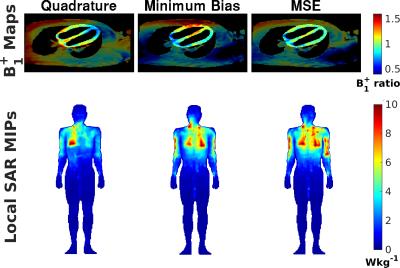
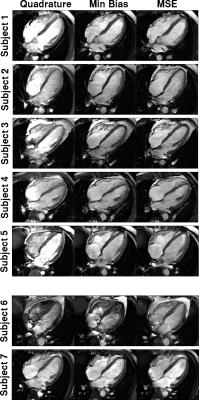
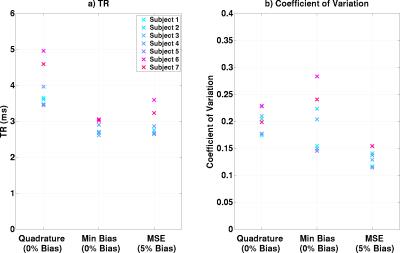
Figure 2a shows minimum TRs achieved in the three scenarios. Both optimisations substantially reduce TR compared with quadrature mode (TR reduced by 1.35±0.31ms) with the minimum bias optimisation performing better. However, minimum bias optimization leads to unpredictable flip-angle uniformity (Figure 2b). Figure 3 shows B$$$_1^+$$$ maps from one subject, illustrating this effect, along with predicted $$$lSARmax$$$ distributions – all limited by 10Wkg^-1. Figure 4 shows bSSFP images for all subjects.

The method can be used with different SAR limits – repeating the optimization for $$$\theta_0$$$=60° with $$$lSARmax$$$=20Wkg^-1 as in Reference 8 leads to the results in Figure 5. In this case minimum TRs of 2.7ms are possible, comparing favourably with the published 3.8ms for the same constraints.

Discussion and Conclusions

Acknowledgements

The research was funded by the following grant:

EPSRC (UK research councils) grant number EP/L00531X/1

References

1. Bieri O, Scheffler K. Fundamentals of balanced steady state free precession. J. Magn. Reson. Imaging. 2013;38:2–11.

2. Schär M, Kozerke S, Fischer SE, Boesiger P. Cardiac SSFP Imaging at 3 Tesla. Magn. Reson. Med. 2004;51:799–806.

3. Brunner DO, Pruessmann KP. Optimal design of multiple-channel RF pulses under strict power and SAR constraints. Magn. Reson. Med. 2010;63:1280–91.

4. Graesslin I, Homann H, Biederer S, Börnert P, Nehrke K, Vernickel P, Mens G, Harvey P, Katscher U. A specific absorption rate prediction concept for parallel transmission MR. Magn. Reson. Med. 2012;68:1664–1674.

5. Eichfelder G, Gebhardt M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn. Reson. Med. 2011;66:1468–76.

6. Vernickel P, Röschmann P, Findeklee C, Lüdeke K-M, Leussler C, Overweg J, Katscher U, Grässlin I, Schünemann K. Eight-channel transmit/receive body MRI coil at 3T. Magn. Reson. Med. 2007;58:381–9.

7. Nehrke K, Bornert P. DREAM-a novel approach for robust, ultrafast, multislice B1 mapping. Magn. Reson. Med. 2012;68:1517–1526.

8. Weinberger O, Winter L, Dieringer MA, et al. Local Multi-Channel RF Surface Coil versus Body RF Coil Transmission for Cardiac Magnetic Resonance at 3 Tesla: Which Configuration Is Winning the Game? PLoS One. 2016;11:e0161863.