0302

Image Reconstruction Algorithm for Motion Insensitive Magnetic Resonance Fingerprinting (MRF)
Bhairav Bipin Mehta1, Dan Ma1, Simone Coppo1, and Mark Alan Griswold1

1Radiology, Case western reserve university, Cleveland, OH, United States

Synopsis

Motion is one of the biggest challenges in clinical MRI. The recently introduced Magnetic Resonance Fingerprinting (MRF) has been shown to be less sensitive to motion. However, it is still susceptible to patient motion primarily occurring in the early stages of the acquisition. In this study, we propose a novel reconstruction algorithm for MRF, which decrease the motion sensitivity of MRF. The evaluation of the algorithm was performed using simulated head tilt and nodding motion, and with prospectively motion corrupted data from healthy volunteers.

Purpose:

Increase robustness of magnetic resonance fingerprinting (MRF)[1] towards patient motion.

Introduction:

Patient motion is ubiquitous in clinical MRI, and in certain situations it is nearly unavoidable. For example, in patient populations such as the elderly, pediatrics, stroke, etc., susceptibility of MR acquisition to patient motion leads to need for anesthesia, lengthening of scan duration or loss of valuable diagnostic or therapeutic information thereby, reducing the value of the exam. Recently, a multi-parametric imaging technique, MRF[1], was introduced, which has been shown to be less sensitive to subject motion than conventional imaging techniques. However, the reconstruction algorithm[1] used in most initial implementations is still susceptible to patient motion primarily occurring in the early stages of the acquisition. In this work, we present an image reconstruction algorithm to further reduce the sensitivity of MRF to patient motion.

Methods:

The general flow of the proposed reconstruction algorithm, referred to as MOtion insensitive magnetic Resonance Fingerprinting (MORF), is as follows:

Start.

Pattern recognition based projection onto dictionary.

while ( (||update(:)||2 / ||current image estimate(:)||2 )< threshold)

$$$\space{\space{\space{\space{\space{\space{}}}}}}$$$Identification of motion corrupted frames.

$$$\space{\space{\space{\space{\space{\space{}}}}}}$$$Motion estimation.

$$$\space{\space{\space{\space{\space{\space{}}}}}}$$$Data consistency.

$$$\space{\space{\space{\space{\space{\space{}}}}}}$$$Pattern recognition based projection onto dictionary.

end

Stop.

The specific details of each sub-sections are as follows:

Pattern recognition: This operation was done using template matching in the same way as described in reference [1].

Identification of motion corrupted frames: The motion corrupted frames were identified using combination of three metrics. Specifically, the normalized mutual information between each map (T1 and T2) and the frames before the pattern recognition operation, and the relative root mean square error (RMSE) between the data before and after pattern recognition were computed. For each of the three metrics, the entire set of frames was divided into two sections using a threshold estimated using Otsu’s method[2]. The section with lower number of frames was considered as motion corrupted. Finally, union of all the motion corrupted frames identified using the three metrics were used for motion estimation.

Motion estimation: The estimation of the rigid-body motion was performed using image registration between low-resolution estimates of each frame with the corresponding frames from the output of the pattern recognition step as the reference. A low-resolution estimate of each frame was generated by applying radially symmetric Hanning window kernel to the motion-compensated (based on the motion estimates from previous iterations) k-space measurements. The windowing kernel parameters were: accept band=10%, transition band=10% and stop band=80%. Additionally, view-sharing with a window size of three was used to further mitigate the undersampling artifacts.

Data consistency was performed using following equation:

$$\bf{m^*}=\bf{m}+\it{\space{F_uR^{-1}}}\space{\bf{d}}-\it{F_uF_u^{-1}}\space{\bf{m}}\space{\space{}}$$

where$$$\space{}\bf{m}\space{}$$$is the input frames,$$$\space{}\it{R}\space{}$$$is the motion registration operator,$$$\space{}\bf{d}\space{}$$$is the measured k-space data,$$$\space{}\it{F_u}\space{}$$$is the undersampled nuFFT[3] combined with coil combination operation.

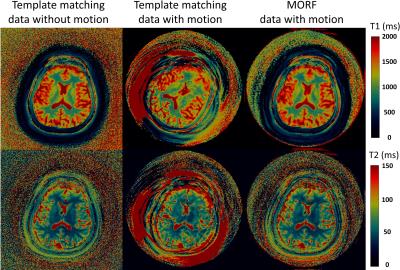
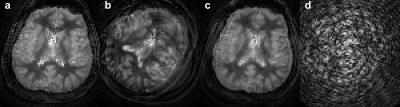
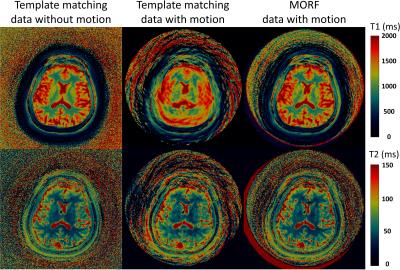
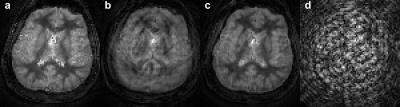
The evaluation of the MORF algorithm was performed by simulating motion in a fully sampled in vivo brain data without motion, acquired using FISP based MRF acquisition[4]. Following types of motion were simulated during the beginning of the MRF acquisition (210 out of 1000 frames corrupted): 1. Tilt: head position starts at 450 and in the middle of the scan rotates to a position at 00; 2. Nodding: continuous head rotation along left-right direction with max rotation of ±150. The motion corrupted data were undersampled (spirals=1; R=48) to estimate the k-space measurements. A dual-density spiral trajectory (FOV=300x300mm2 and matrix=256x256) with a density of 2 and 48 arms was used in this study. All imaging was performed on 3T (Skyra, Siemens) after informed consent. Additionally, prospectively motion corrupted MRF data were acquired from a healthy volunteer for evaluation of the MORF algorithm. The subject was requested to move back and forth in the left-right direction in the initial ~3s of a 13.5s FISP based MRF acquisition.

Results & Discussions:

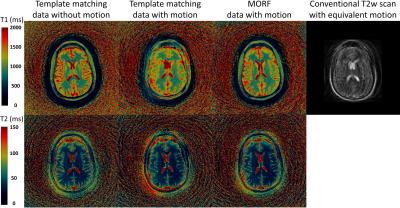
Figures 1 (maps) and 2 (motion corrupted frames) show results from experiment with simulated head tilt motion. Figures 3 (maps) and 4 (motion corrupted frames) show results from experiment with simulated head nodding motion. In both the experiments we see MORF results are closer to ground truth and present minimal errors. Figure 5 shows example results from prospectively motion corrupted in vivo scans. Again, MORF results show effective suppression of motion artifacts and closely resemble the results from data without motion. The discrepancy in the slice location between acquisitions with and without motion might be due to inter-scan subject motion.

Conclusion:

The proposed MORF reconstruction algorithm noticeably decreases the sensitivity of MRF to subject motion; thereby reducing the loss of diagnostic and therapeutic information, need for anesthesia and length of the procedure, which in turn improves the value of the exam.

Acknowledgements

The authors would like to acknowledge funding from Siemens Healthcare and NIH grants NIH 1R01EB016728 and NIH 5R01EB017219. This work made use of the High Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University.

References

1. Dan Ma et al,”Magnetic Resonance Fingerprinting” Nature 2013; 495(7440):187

2. Otsu, N., "A Threshold Selection Method from Gray-Level Histograms," IEEE Transactions on Systems, Man, and Cybernetics, Vol. 9, No. 1, 1979, pp. 62-66.

3. Pipe JG, Matlab nuFFT Toolbox.

4. Yun Jiang et al,”MR fingerprinting using fast imaging with steady state precession (FISP) with spiral readout” MRM 2015; 74(6):1621.

Figures

Figure 1: Example mapping results from simulated head tilt motion experiment. First column: maps using template matching[1] generated from data without simulated motion; Second column: maps using template matching generated from data with simulated head tilt motion; Third column: maps using MORF generated from data with simulated head tilt motion. Template matching results present severe motion artifacts. However, MORF results closely resemble to ground truth with minimal errors.

Figure 2: Example frames from the motion corrupted segment from simulated head tilt motion experiment. A: output frames using template matching generated from data without simulated motion; B: output frames using template matching generated from data with simulated head tilt motion; C: output frames using MORF generated from data with simulated head tilt motion; D: undersampled frames from data with simulated head tilt motion. Template matching present severe motion artifacts while MORF restores the orientation with minimal errors. (The frames were resampled to 128x128 and then cropped to reduce the file size)

Figure 3: Example mapping results from simulated head nodding motion experiment. First column: maps using template matching generated from data without simulated motion; Second column: maps using template matching generated from data with simulated head nodding motion; Third column: maps using MORF generated from data with simulated head nodding motion. Again, template matching results present motion artifacts which are significantly minimized in MORF results.

Figure 4: Example frames from the motion corrupted segment from simulated head nodding motion experiment. A: output frames using template matching generated from data without simulated motion; B: output frames using template matching generated from data with simulated head nodding motion; C: output frames using MORF generated from data with simulated head nodding motion; D: undersampled frames from data with simulated head nodding motion. Template matching present severe motion artifacts while MORF restores the orientation with minimal errors. (The frames were resampled to 128x128 and then cropped to reduce the file size)

Figure 5: Results from prospectively motion corrupted (~22%) invivo experiment. First column: template matching maps from a separate scan without subject motion; Second column: template matching maps using data with subject motion; Third column: MORF maps using data with subject motion; Fourth column: conventional T2w-TSE with equivalent subject motion. It should be noted that the discrepancy in the brain structure between data with and without motion might be due to change in the imaging location because of inter-scan subject motion. The results are consistent with simulated motion experiments. MORF noticeably increases the robustness of MRF acquisition towards subject motion.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0302