0301

Motion correction in volumetric brain imaging based on DISORDER: Distributed and Incoherent Sample Orders for Reconstruction Disentanglement using Encoding Redundancy

Lucilio Cordero-Grande¹, Giulio Ferrazzi¹, Rui Pedro AG Teixeira¹, Hassan Shahzad², Anthony N Price¹, and Joseph V Hajnal¹

¹Division of Imaging Sciences and Biomedical Engineering, King’s College London, London, United Kingdom, ²Electrical Engineering Department, COMSATS Institute of Information Technology, Islamabad, Pakistan

Synopsis

The DISORDER framework for motion tolerant reconstruction in parallel volumetric brain imaging synergistically combines distributed and incoherent sample orders with a joint retrospective motion estimation and reconstruction technique based on encoding redundancy provided by coil arrays. DISORDER is fully data-based, does not make use of external sensors or acquisition of navigators, does not require data rejection, and can be applied to different sampling schemes and imaging modalities. In-vivo application of DISORDER has shown robustness against extreme and continuous motion in low resolution images and moderate and continuous motion in standard and high resolution images as well as slightly improved contrast properties in high resolution motion images without deliberate motion.

Purpose

Tolerance against motion is desirable in volumetric brain imaging for preventing artifacts¹ and performing high resolution studies². In³ we presented a fully data-driven reconstruction method for retrospective head motion correction that does not use external sensors or acquisition of navigators and can be applied to any sampling scheme. Here, we show that the performance of this method can be greatly boosted by using optimized orderings of $$$\mathbf{k}$$$-space traversals, creating a framework to correct for head motion on a variety of spatio-temporal scales and image modalities.

Methods

Retrospective motion corrected brain reconstruction for parallel MRI using a rigid model is posed as $$$(\hat{\mathbf{x}},\hat{\boldsymbol{\theta}})=argmin_{\mathbf{x},\boldsymbol{\theta}}f(\mathbf{x},\boldsymbol{\theta})$$$, with $$$f(\mathbf{x},\boldsymbol{\theta})=\|\mathbf{A}\boldsymbol{\mathcal{F}}\mathbf{S}\mathbf{T}_{\boldsymbol{\theta}}\mathbf{x}-\mathbf{y}\|_2^2$$$, where $$$\mathbf{y}$$$ denotes the measurements, $$$\mathbf{x}$$$ the image to be reconstructed, $$$\mathbf{S}$$$ the coil sensitivity matrix, $$$\mathbf{T}_{\boldsymbol{\theta}}$$$ the rigid transformation matrix described by the motion parameters $$$\boldsymbol{\theta}$$$, $$$\boldsymbol{\mathcal{F}}$$$ the Fourier transform matrix, and $$$\mathbf{A}$$$ the applied sampling matrix. This problem is solved by alternating between reconstructing $$$\mathbf{x}$$$ for a fixed $$$\boldsymbol{\theta}$$$ (least-squares) via conjugate gradient⁴ and estimating $$$\boldsymbol{\theta}$$$ for a fixed $$$\mathbf{x}$$$ (maximum likelihood) via Newton-type methods³. Its basic assumption is that the image acquisition can be temporally decomposed into a set of motion states $$$s\in\mathcal{S}$$$ for which motion is assumed to be negligible; i.e., for a given set of acquired samples $$$\mathbf{A}_s$$$ the motion state of the imaged structure is modelled by $$$\boldsymbol{\theta}_s$$$, which may correspond to all or only part of an acquired shot in multi-shot sequences.

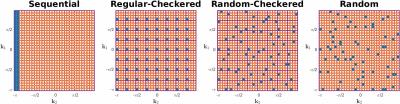
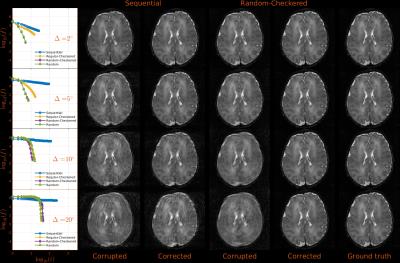
The simulations in³ showed that global convergence of the aligned reconstruction is strongly sensitive to the traversal order. Here, simulations are extended to gain evidence of optimal Cartesian sampling ordering in volumetric imaging, where measurements cover a 2D phase-encode space. Mimicking this undersampled 2D space and looking for concise conclusions, the simulations investigate the ability to retrieve 2D rotational motion for sequential (standard manufacturer sampling), regular-checkered, random-checkered, and purely random $$$\mathbf{k}$$$-space traversals (Figs. 1 and 2). The non-sequential orderings proposed are aimed at maximizing the sensitivity to motion induced inconsistencies by sampling a diverse set of harmonics in a short period of time.

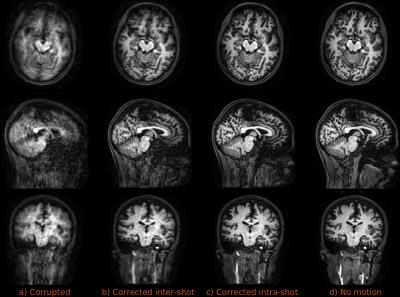
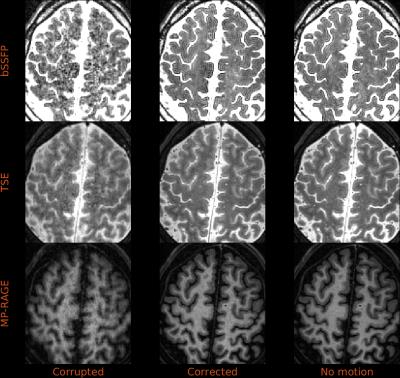
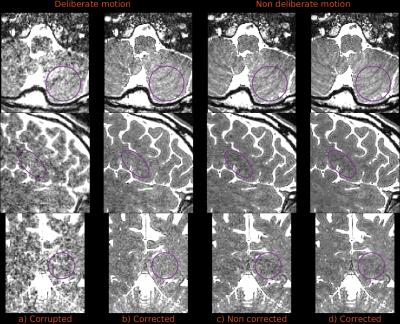
These schemes were implemented on a Philips 3T Achieva for in-vivo application in virtually any 3D sequence. Testing demonstrated that fully random sampling resulted in intrusive artifacts attributed to Eddy currents, whereas random-checkered zig-zag patterns were largely free of such problems⁵ while allowing matched contrast with standard sampling and presenting interesting properties to resolve motion (see caption of Fig. 1). Three experiments, using a standard 32-channel coil, are covered here: a) low resolution / extreme motion, where a volunteer was asked to perform extreme and continuous motion of the head during the whole 1.5mm isotropic MP-RAGE scan (Fig. 3); b) standard resolution / moderate motion, where the volunteer continuously and smoothly moved the head during 1mm isotropic bSSFP, TSE and MP-RAGE scans (Fig. 4); and c) high resolution scan, 0.7mm isotropic bSSFP, with and without deliberate motion (Fig. 5).

Results

Simulations in Fig. 2 show that all regular-checkered, random-checkered, and purely random traversals substantially outperform sequential traversal. In-vivo reconstructions of Figs. 3 and 4 are almost indistinguishable from motion-free counterparts. Temporal resolvability of motion varies with the type of sequence and spatial resolution, but was always below the time required for a full checkered $$$\mathbf{k}$$$-space sweep, allowing some degree of intra-shot corrections for multi-shot sequences (Fig. 3c vs. 3b). Reconstructions of high resolution data (Fig. 5) are also effective in case of deliberate motion (Fig. 5b vs. 5a) and show slightly improved contrast compared to non-corrected reconstructions for non deliberate motion (Figs. 5d vs. 5c).

Discussion

Simulation results show that a distributed sampling ordering of the $$$\mathbf{k}$$$-space supports more effective motion correction than sequential ordering. In-vivo tests show that the combination of the proposed sampling and reconstruction techniques is highly effective, even in cases of extreme and continuous head motion, suggesting that the proposed approach could be used for motion correction in non-compliant subjects and to improve data quality in the general population¹. Experiments also show that the framework holds promise for motion resolvability of ultra-high resolution MRI. This approach is compatible with parallel imaging acceleration but Eddy currents and SNR may be limiting factors and thus care is needed to avoid Nyquist violation problems introduced by rotations. Problem complexity is $$$O(N^5)$$$ with $$$N$$$ being the image grid size, which imposes computational limitations.

Conclusion

We have shown that DISORDER provides robustness against motion for brain MRI. The proposed method is fully data-driven, can accommodate short lived motion states independent of shot structure, does not require data rejection, and can be applied to different volumetric modalities.

Acknowledgements

The authors acknowledge financial support from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013) / ERC Grant Agreement n.319456. This work was also supported by Medical Research Council (MRC) strategic grant MR/K006355/1 and the Department of Health via the National Institute for Health Research(NIHR) comprehensive Biomedical Research Centre award to Guy’s & St Thomas’ NHS Foundation Trust in partnership with King’s College London and King’s College Hospital NHS Foundation Trust. The authors also acknowledge the Department of Perinatal Imaging & Health at King’s College London.

References

1. Andre J, Bresnahan B, Mossa-Basha M, et al. Towards quantifying the prevalence, severity, and cost associated with patient motion during clinical MR examinations. J Am Coll Radiol. 2015;12(7):689-695.

2. Budde J, Shajan G, Scheffler K, and Pohmann R. Ultra-high resolution imaging of the human brain using acquisition-weighted imaging at 9.4T. NeuroImage. 2014;86(1):592-598.

3. Cordero-Grande L, Teixeira RPAG, Hughes EJ et al. Sensitivity encoding for aligned multishot magnetic resonance reconstruction. IEEE Trans Comput Imaging. 2016;2(3):266-280.

4. Batchelor PG, Atkinson D, Irarrazaval P, et al. Matrix description of general motion correction applied to multishot images. Magn Reson Med, 2005;54(5):1273-1280.

5. Tsao J, Kozerke S, Boesiger P, and Pruessmann KP. Optimizing spatiotemporal sampling for k-t BLAST and k-t SENSE: application to high resolution real-time cardiac steady-state free precession. Magn Reson Med, 2005;53(6):1372-1382.

Figures

Trajectory orderings of 32x32 $$$\mathbf{k}$$$-space for an exemplary 16-shot sequence and checkered tessellation of 4x4. Sequential traversal captures a limited amount of spectral information in each shot (or equivalent time for non shot-based sequences) whereas the information is richer for the other traversals. Random-checkered traversal provides a compromise between spatially balanced coverage of regular-checkered traversal and temporally incoherent coverage of fully random traversal.

Example of the convergence (left) of the joint alignment and reconstruction for different traversals ($$$i$$$ denotes the iteration number). Simulated motion for each state is sampled independently from an uniform distribution of rotations in the range $$$[−\Delta/2,\Delta/2]$$$, with $$$\Delta=\{2^{\circ},5^{\circ},10^{\circ},20^{\circ}\}$$$ (from top to bottom). 64 motion states are used for a 128x128 $$$\mathbf{k}$$$-space and 8x8 tessellation corresponding to the sampling structure of motion states. Simulated images and sensitivities are taken from a motion-free TSE sequence. Correction from sequential traversal is much slower, such as for $$$\Delta=\{2^{\circ},5^{\circ}\}$$$, and may not converge to a satisfactory solution, as clearly appraised for $$$\Delta=\{10^{\circ},20^{\circ}\}$$$.

Example of correction in an extreme and continuous motion setting: 3 repeats of a MP-RAGE 1.5mm isotropic (elliptic shutter) SENSE 2x2 TFE factor 121 and T_R 8.3ms. As a first approximation, one motion state is assumed for each of the 30 shots that comprise each repeat with a 6x5 checkered tessellation built accordingly (Fig. 3b). Visual data quality improvement has been observed up to a 16x subdivision of each shot, which gives a motion estimate every 62.8ms (Fig. 3c) using only 7-8 readouts, with no visual differences observed by running the method at a finer temporal resolution.

Example of correction in a moderate and continuous motion setting for different modalities at 1mm isotropic (elliptic shutter), SENSE 1.5x1.5. bSSFP with T_R 3.8ms and 5x5 tessellation (selected considering Eddy currents limitations). TSE with TSE factor 141, T_E 1.15ms, 100 shots and 10x10 tessellation. MP-RAGE with TFE factor 141, T_R 10ms, 100 shots and 10x10 tessellation. Visual data quality improvement has been observed up to temporal subdivision of acquisition into 400 motion states, temporal resolution of 134.0ms (bSSFP), 200 motion states, temporal resolution of 232.7ms (TSE), and 400 motion states, temporal resolution of 352.5ms (MP-RAGE).

Examples of correction in moderate and continuous and non deliberate motion settings: bSSFP 0.7mm isotropic (elliptic shutter), SENSE 1.5x1.5, with T_R 4.9ms and 5x5 tessellation (selected considering Eddy currents limitations). For non deliberate motion, visual data quality improvement has been observed up to temporal subdivision of acquisition into 50 motion states, temporal resolution of 2910.8ms (Fig. 5d vs. 5c), with no visual differences observed by running the method at a finer temporal resolution. For deliberate motion, visual data quality improvement has been observed up to 200 motion states, temporal resolution of 725.5ms (Fig. 5b vs. 5a).

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0301