Synopsis

We estimate microstructural features of the nervous tissues from diffusion-weighted MRI by using sparse optimization techniques on a dictionary of pre-computed Monte Carlo signals, which more faithfully describe the complex diffusion process in the extra-axonal space of the white matter. The method is validated on synthetic data including single and crossing fibers and on an in vivo rat spinal cord model of Wallerian degeneration. We obtain in vivo microstructural estimates that can be directly related to histological evidence whereas the traditional closed-form formula models DIAMOND and NODDI yield results that are more challenging to interpret physically.

Purpose

Most diffusion-weighted MRI (DW-MRI) microstructure imaging approaches use closed-form formulas of the DW signal attenuation based on simplifying assumptions on the tissue or the diffusion processes and only use Monte Carlo (MC) simulations as synthetic ground-truth for validation.

We instead investigate the estimation of microstructural features by using a dictionary of pre-computed realistic MC diffusion signals that more faithfully describe the complex diffusion process in the extra-axonal space. We evaluate this approach on an in vivo rat spinal cord model of Wallerian degeneration, compare results to those obtained with the DIAMOND¹ and NODDI² closed-form formulas and investigate an extension to multi-fascicles in silico.

Methods

General signal model: We assume that the normalized DW-MRI signal in a voxel$$E=\frac{T_{WM}\sum_{k=1}^{K}\nu_kE_k(\mathbf{n}_k)+\nu_{CSF}T_{CSF}E_{CSF}}{(1-\nu_{CSF})T_{WM}+\nu_{CSF}T_{CSF}}=\sum_{k=1}^{K}w_kE_k(\mathbf{n}_k)+w_{CSF}E_{CSF}$$arises from the contributions of$$$\;K\;$$$fascicles of axons of orientations$$$\;\mathbf{n}_1,\dots,\mathbf{n}_K\;$$$ and an isotropic CSF compartment, neglecting water exchange between compartments. The effective DW-MRI weights$$$\;w_k\;$$$are the volume fractions$$$\;\nu_k\;$$$weighted by the T2-relaxation factors$$$\;T=\exp\left(-TE/T2\right)\;$$$at echo time TE and the signal$$$\;E_k\;$$$of each fascicle arises from MC simulations of water molecules in biologically-relevant substrates, typically featuring geometrical arrangements of cylindrical axons.

Estimation: We consider fascicles represented by a hexagonal packing^3-5 of straight cylinders and precompute single-fascicle signals for$$$\;N=832\;$$$combinations of radius index$$$\;r\;$$$(from$$$\;0.8\;$$$µm to$$$\;7\;$$$µm by steps of$$$\;0.2\;$$$µm) and density index$$$\;f\;$$$(from$$$\;0.12\;$$$to $$$\;0.87\;$$$by steps of$$$\;0.03$$$)$$$\;$$$with efficient MC simulations leveraging exact analytical formulas for molecules trapped inside cylinders^6,7. We then estimate the microstructural parameters in each voxel by rotating the signals along the orientations$$$\;\mathbf{n}_k\;$$$estimated a priori using a DIAMOND sub-routine¹ and by solving the problem$$\begin{equation*}\begin{array}\\\mathbf{w}^*=&\underset{\begin{array}[l]\\\mathbf{w}\geq0\\\left|\mathbf{w}\right|_1=1\end{array}}{\text{argmin}}&\left\|y-\begin{bmatrix}F_1|\dots|F_K|E_{CSF}\end{bmatrix}\cdot\begin{bmatrix}\mathbf{w}_1\\\vdots\\\mathbf{w}_K\\w_{CSF}\end{bmatrix}\right\|_2^2\\&&\\&\text{subject}\;\text{to}&\left|\mathbf{w}_k\right|_{0}=1,{\quad}k=1,\dots,K,\\\end{array}\end{equation*}$$where$$$\;y\;$$$contains the DW-MRI acquisitions and the sparsity constraints on the sub-vectors$$$\;\mathbf{w}_k\;$$$guarantee that only one fascicle configuration$$$\;(r,f)\;$$$per sub-dictionary$$$\;F_k=\left[E\left(r_1,f_1,\mathbf{n}_k\right)|\dots|E\left(r_N,f_N,\mathbf{n}_k\right)|E_{CSF}\right]\;$$$contributes to the measured signal. For$$$\;K{\leq}2$$$, an exhaustive search of every possible combinations of atoms is performed. For$$$\;K=3$$$, sparsity is enforced via l1-reweighted schemes⁸ for computational tractability.

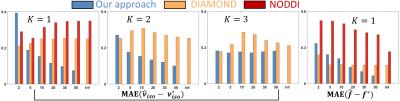
Synthetic experiments: Considering a PGSE protocol containing 6 shells of 36 non-colinear gradient directions at b-values $$$300,700,1500,2800,4500\;$$$and$$$\;6000\,\textrm{s/mm²};\;TE=23\,\textrm{ms},\delta=4.5\,\textrm{ms}\;$$$and$$$\;\Delta=12\,\textrm{ms},\;$$$we simulated DW-MRI signals from our signal model on 3000 synthetic voxels containing up to 3 fascicles and corrupted them with non-central Chi noise (Ncoils=4, SNR=2-50). We assessed the ability of our method, DIAMOND and NODDI to estimate various parameters in terms of mean absolute error (MAE) with the ground-truth values.

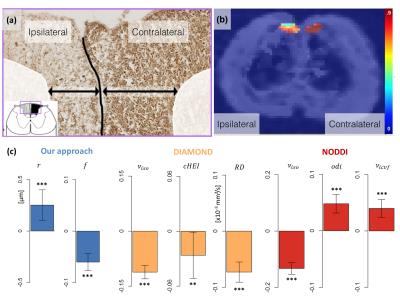
In vivo rat data and histology: Three rats underwent unilateral rhizotomy at vertebral levels L2-L3 causing Wallerian degeneration in the ipsilateral gracile fasciculus (GF) of the spinal cord, three other rats serving as controls. Acquisitions were performed in vivo 51 days post-surgery at 11.7T (Bruker BioSpec) on all 6 rats using the above-described protocol. The rats were then sacrificed and SMI312 immunostaining revealed a notable axonal loss in the ipsilateral part of the GF primarily affecting small axons, while the contralateral part remained little affected (Figure 2a). For all microstructural properties$$$\;y\;$$$from all 3 methods, we evaluated the regression model:$$y=\beta_0+\beta_{\textrm{surgery}}{\cdot}S+\beta_{\textrm{ipsi}}{\cdot}I+\beta_{\textrm{effect}}{\cdot}S{\cdot}I,$$where$$$\;S\;$$$and$$$\;I\;$$$are binary variables indicating surgery or ipsilateral side, incorporating healthy controls, and where$$$\;\beta_{\textrm{effect}}\;$$$is the effect of interest which should be large only for parameters physically impacted by the surgery.

Results and discussion

Our method shows consistent results in the 1 and 2-fascicle configurations as the MAE on the isotropic volume fraction$$$\;\nu_{iso}\;$$$(our$$$\;\nu_{CSF}$$$) and axonal density index$$$\;f\;$$$converges to$$$\;0\;$$$with increasing SNR (Figure 1) but does not exhibit satisfactory convergence with 3 fascicles. The NODDI and DIAMOND estimates do not necessarily converge to the ground-truth values even with one fascicle, suggesting potentially complex relationships between their parameters and the underlying tissue features.

In the in vivo rat experiment, we set$$$\;\nu_{iso}=0\;$$$in our method as our manual segmentation of the GF did not contain CSF, reducing our estimation to a single-fascicle dictionary lookup⁹. Unsurprisingly, significant differences are observed with all models, reflecting the dramatic alteration of the microstructure caused by Wallerian degeneration. However, the challenge here is to identify the sources of those changes. Figures 2 shows that our dictionary-based approach attributes the difference to a decrease in intracellular volume fraction and a slight increase in axonal radius, in keeping with the histology. In contrast, both DIAMOND and NODDI ascribe the difference in diffusion signal to changes in a range of parameters (Figures 2c), making the interpretation of the findings more challenging and possibly misleading.

Conclusion

Acknowledgements

References

[1] Scherrer, Benoit, et al. "Characterizing brain tissue by assessment of the distribution of anisotropic microstructural environments in diffusion-compartment imaging (DIAMOND)." Magnetic resonance in medicine (2015).

[2] Zhang, Hui, et al. "NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain." Neuroimage 61.4 (2012): 1000-1016.

[3] Alexander, Daniel C., et al. "Orientationally invariant indices of axon diameter and density from diffusion MRI." Neuroimage 52.4 (2010): 1374-1389.

[4] Xu, Junzhong, et al. "Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy." NeuroImage 103 (2014): 10-19.

[5] Sepehrband, Farshid, et al. "Towards higher sensitivity and stability of axon diameter estimation with diffusion-weighted MRI." NMR in Biomedicine 29.3 (2016): 293-308.

[6] Cook, P. A., et al. "Camino: open-source diffusion-MRI reconstruction and processing." 14th scientific meeting of the international society for magnetic resonance in medicine. Vol. 2759. Seattle WA, USA, 2006.

[7] Rensonnet, Gaëtan, et al. "A hybrid method for efficient and accurate simulations of diffusion compartment imaging signals." 11th International Symposium on Medical Information Processing and Analysis (SIPAIM 2015). International Society for Optics and Photonics, 2015.

[8] Candes, Emmanuel J., Michael B. Wakin, and Stephen P. Boyd. "Enhancing sparsity by reweighted l 1 minimization." Journal of Fourier analysis and applications 14.5-6 (2008): 877-905.

[9] Nilsson, Markus, et al. "Evaluating the accuracy and precision of a two-compartment Kärger model using Monte Carlo simulations." Journal of Magnetic Resonance 206.1 (2010): 59-67.