0283

Multi-compartment microscopic diffusion imaging with oscillating gradients: simulation validation and application in multiple sclerosis patients

Hua Li^1,2, Enrico Kaden³, Daniel C. Alexander³, John C. Gore^1,2, Bagnato R. Francesca^1,2,4, and Junzhong Xu^1,2

¹Institute of Imaging Science, Vanderbilt University, Nashville, TN, United States, ²Department of Radiology and Radiological Sciences, Vanderbilt University, Nashville, TN, United States, ³Centre for Medical Image Computing, University College London, United Kingdom, ⁴Neuroimmunology Division/Neuroimaging Unit, Department of Neurology, Vanderbilt University, Nashville, TN, United States

Synopsis

Microscopic diffusion imaging using spherical mean technique (SMT) and oscillating gradient spin echo (OGSE) was applied in multiple sclerosis patients, along with computer simulation validation. The results suggested that there are significant decreases of axon volume fraction in multiple sclerosis patients compared with contralateral normal tissue.

Purpose

Diffusion tensor imaging (DTI) has been widely used clinically to probe pathological changes in various neurodegenerative diseases, but sometimes the interpretation of DTI data is ambiguous and not clearly related to underlying microstructural properties of tissues. Various advanced multi-compartment diffusion models have been developed to characterize specific intra- and extra-axonal compartments in white matter (WM), but are typically confounded by complex 3D fiber orientations in the brain including fiber crossings, dispersion, undulation, and bending. Recently, a new method for microscopic diffusion imaging based on the spherical mean technique (SMT) [1, 2] has been developed which is capable of removing the influence of neurite orientation distribution and thus provides more direct estimates of the microscopic tissue structure. However, the accuracy of SMT for estimating specific tissue structure properties such as intra-axonal volume fraction and diffusivity has not been comprehensively validated, and it has not been implemented in human imaging to characterize pathological changes in patients. In this study, we extend SMT by including additional acquisitions using oscillating gradient spin echo (OGSE) sequences to probe a broader range of diffusion times, validate the accuracy of SMT using computer simulations, and report the first application of SMT in multiple sclerosis patients.

Methods

Theory: The two-compartment mean diffusion signal using SMT in WM is [1, 2] $$$S=v_{ax}S_{ax}+(1-v_{ax})S_{ex}$$$, where $$$S_{ax}=\frac{\sqrt{\pi}erf(\sqrt{bD_{ax}})}{2\sqrt{bD_{ax}}}$$$ and $$$S_{ex}=exp(-bD_{\perp,ex})\frac{\sqrt{\pi}erf(\sqrt{b(D_{ax}-D_{\perp,ex})})}{2\sqrt{b(D_{ax}-D_{\perp,ex})}}$$$ are the intra- and extra-axonal diffusion signals per volume after taking the spherical mean over all gradient directions, respectively [1]. $$$D_{\perp,ex}=(1-v_{ax})D_{ax}+\beta_{ex}\cdot f$$$ [3,4]. Three microstructure parameters will be fit: $$$v_{ax}$$$and $$$D_{ax}$$$ are intra-axonal water fraction and diffusivity, respectively, and $$$\beta_{ex}$$$ is the dispersion rate of $$$D_{\perp,ex}$$$ with respective to diffusion gradient frequency [4]. Note that due to the relatively long diffusion times, $$$D_{\perp,ax}$$$ is assumed to be zero for all PGSE and OGSE acquisitions.

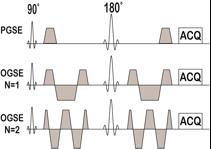
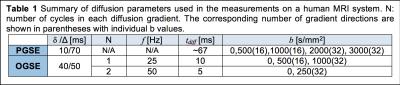
Imaging: Pulse sequences are shown in Fig.1, and the diffusion related parameters are summarized in Table 1. Three MS patients were scanned using a Philips Achieva 3T scanner with a 32-channel head coil. TE=124ms; FOV=216×216mm; reconstructed in-plane resolution = 1.93×1.93 mm; 30 slices; slice thickness=3 mm; single shot EPI without SENSE. High resolution (0.4×0.4×3mm) T1/T2 images were acquired in the same session, and regions of interest of multiple sclerosis lesions and contralateral normal appearing WM (NAWM) were selected based on T1/T2 images. All images were then co-registered and analyzed using FSL and home-written MATLAB code.

Simulation: Tissue models consisting of randomly packed parallel cylinders (in which cylinder diameters obey a Gamma distribution with a mean size of ~ 2 μm) with five different intra-axonal volume fractions were generated for computer simulations (see Fig.2). The intrinsic diffusivity was 2.5 μm²/ms everywhere. All experimental parameters were the same as those in the human imaging, and parameter fittings were repeated 100 times with random noise added at SNR = 20 each time.

Results

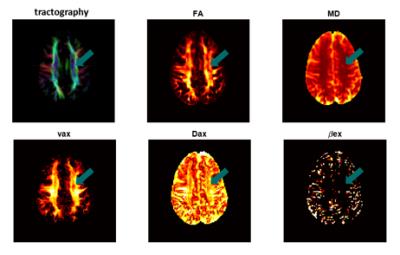
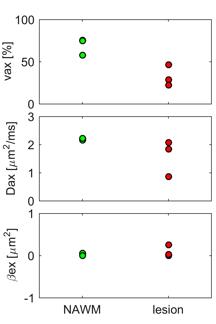
Fig.3 shows a comparison of fitted $$$v_{ax}$$$ (top), $$$D_{ax}$$$ (middle) and $$$\beta_{ex}$$$ (bottom) from simulated data with the corresponding ground-truth values. It is obvious that with reasonable SNR=20, our method can reliably estimate $$$v_{ax}$$$ and $$$D_{ax}$$$ over a broad range of $$$v_{ax}$$$ (32.9% – 70.1%). Note that although the means of $$$\beta_{ex}$$$ were estimated around 1-2 μm², one-way ANOVA provides p = 0.72, indicating $$$\beta_{ex}$$$ may not be significantly different from zero, far below ground truth values. This is consistent with patient imaging results, suggesting $$$\beta_{ex}$$$ may not be reliably fit in the central nervous system. Multi-parametric maps of a representative slice from a MS patient are shown in Fig.4, and Fig.5 shows the decrease of both $$$v_{ax}$$$ and $$$D_{ax}$$$ in lesions from three MS patients compared with corresponding contralateral NAWM.

Conclusion

In the current study, we extend the microscopic diffusion imaging MDI with SMT by adding additional OGSE acquisitions, and validated the accuracy of MDI in estimating $$$v_{ax}$$$ and $$$D_{ax}$$$ over a broad range of $$$v_{ax}$$$ (32.9% - 70.1%). We also report the first application of MDI in MS patients, and observed the significant decreases of $$$v_{ax}$$$ and $$$D_{ax}$$$ in MS lesions compared with contralateral NAWM.

Acknowledgements

R01CA109106, R01CA173593, and K25CA168936 for funding.

References

[1] E. Kaden, N.D. Kelm, R.P. Carson, M.D. Does, D.C. Alexander, Multi-compartment microscopic diffusion imaging, NeuroImage, 139 (2016) 346-359. [2] E. Kaden, F. Kruggel, D.C. Alexander, Quantitative mapping of the per-axon diffusion coefficients in brain white matter, Magn Reson Med, 75 (2016) 1752-1763. [3] A. Szafer, J. Zhong, J.C. Gore, Theoretical model for water diffusion in tissues, Magn Reson Med, 33 (1995) 697-712. [4] J. Xu, H. Li, K.D. Harkins, X. Jiang, J. Xie, H. Kang, M.D. Does, J.C. Gore, Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy, Neuroimage, 103 (2014) 10-19. [5] A.T. Van, S.J. Holdsworth, R. Bammer, In vivo investigation of restricted diffusion in the human brain with optimized oscillating diffusion gradient encoding, Magn Reson Med, 71 (2014) 83-94.

Figures

Fig.1 Diagrams of pulse sequences used on regular whole-body MRI systems. In addition to SMT with conventional PGSE acquisitions, two OGSE acquisitions with oscillating trapezoidal gradients [5] were used to probe shorter diffusion times.

Fig.2 Cross sections of computer-generated tissues consisting of parallel cylinders. (cylinder diameters obey Gamma distribution with a mean size of ~ 2 μm) with five different intra-cylinder volume fractions.

Fig.3 The comparison of fitted v_ax (top), D_ax (middle) and β_ex (bottom) from simulated data with ground-truth values.

Fig.4 A representative slice of parametric maps from a MS patient. The arrows indicate the lesion.

Fig.5 The comparison of SMT-derived parameters in the contralateral NAWM and the lesions from three MS patients.

Table 1.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0283