0282
Universal power-law scaling of water diffusion in human brain defines what we see with diffusion MRI1Center for Biomedical Imaging, New York University School of Medicine, New York City, NY, United States
Synopsis
Here we identify a universal power-law scaling behavior of the diffusion MRI signal on a clinical scanner. This specific functional form provides a defining signature of water confined within narrow sticks establishing that exchange between intra- and extra-axonal water is not relevant, and the fraction of fully restricted water is negligible in the clinically accessible regime. The observed scaling for the first time in vivo validates the key ingredient specific to the microstructural models of MRI signal from neuronal tissue and enables the in vivo quantification of intra-axonal properties.
Introduction
Diffusion MRI (dMRI) is the only non-invasive imaging modality capable of investigating cellular structure and sensing the restrictions by cell architecture. Interpreting the macroscopic dMRI signal in terms of microscopic cellular parameters in vivo is indirect, and is based on biophysical models of diffusion1. So far, the fundamental building block of diffusion models in the brain conjectured over the past decade – the compartmentalization of water into effectively narrow impermeable “sticks” representing axons2-6 (Figure 1) – has not been validated in vivo. Our work is devoted to establishing this paradigm, and to further employing it for quantifying axonal properties in humans by revealing a universal non-analytic $$$b^{-1/2}$$$ power law scaling of the dMRI signal at $$$b$$$-values up to $$$10\,\mathrm{ms/\mu\,m^2}$$$.Experiment
Four healthy volunteers underwent imaging on a Siemens Prisma 3T MR scanner using a 64-channel receiver head coils with an echoplanar readout diffusion-weighted sequence. Diffusion-weighting was applied along 64 isotropically distributed gradient directions for each of the 21 $$$b$$$-values that were equidistantly distributed in the range $$$[0, 10\,\mathrm{ms/\mu m^2}]$$$. Following imaging parameters were kept constant throughout the data acquisition sequence: $$$\mathrm{TR/TE}: 4000/105\,\mathrm{ms}$$$, matrix: $$$80\times\,80$$$, NEX=1, in-plane resolution: $$$3\times\,3 \,\mathrm{mm^2}$$$, slice thickness: $$$3\,\mathrm{mm}$$$, slices=38. The signal was averaged over 64 diffusion directions per $$$b$$$-shell to boost the signal-to-noise ratio after denoising7 and correction for Gibbs ringing8, eddy current distortions, and the Rician signal bias9.Experimental Results and Theoretical Interpretation
The main experimental observation of this abstract (Figure 2) is the universal power-law form6,10
$${S}(b\rightarrow\infty)\simeq\beta\cdot\,b^{-\alpha}\,+\,\gamma\quad(1)$$
of the dMRI signal in human white matter (WM), with exponent $$$\alpha\,=\,1/2$$$. Here we use diffusion time $$$t\approx\,50\,$$$ms as available on clinical scanners, and diffusion weightings up to $$$b\, =\,10\,\mathrm{ms/\mu m^2}$$$.
To understand why this asymptotic power-law originates from the intra-axonal water, consider the signal (normalized to $$$S|_{b=0}\equiv\,1$$$):
$$S(\mathbf{\hat{g}},\,b)\,=\,f\int\,d\mathbf{\hat{n}} \mathcal{P}(\mathbf{\hat{n}}) \psi_\mathbf{\hat{n}}(\mathbf{\hat{g}},b)+\gamma\,+S^\mathrm{eas}(\mathbf{\hat{g}},b),\quad(2)$$
in the unit direction $$$\mathbf{\hat{g}}$$$. The first, intra-axonal term comes from the collection of narrow channels ("sticks") representing axons and possibly glial cell processes, with net water fraction $$$f$$$, and parameterized by the orientational distribution function (ODF) $$$\mathcal{P}(\mathbf{\hat{n}})$$$ (Figure 1). If the overarching brain dMRI modeling assumption is correct, the signal (stick response function) $$$\psi_\mathbf{\hat{n}}(\mathbf{\hat{g}},b)$$$ from water confined within a stick pointing in the direction $$$\mathbf{\hat{n}}$$$, can be approximated by a simple Gaussian one-dimensional diffusion propagator $$$\psi_\mathbf{\hat{n}}(\mathbf{\hat{g}},b)\equiv\,e^{-bD_a^\parallel (\mathbf{\hat{g}}\cdot\mathbf{\hat{n}})^2}$$$. In the limit $$$bD_a^\parallel\gg\,1$$$, this response function yields a non-negligible contribution only from axons falling within a thin pancake $$$|\mathbf{\hat{n}}\cdot\mathbf{\hat{g}}\rm|\lesssim(bD_a^\parallel)^{-1/2}$$$ nearly transverse to $$$\bf\hat{g}$$$, whose thickness scaling as $$$b^{-1/2}$$$ results in the aforementioned asymptotic form (1).
It is essential, for the power-law scaling (1) to hold, and to originate solely from intra-stick water, that the dMRI signal exactly transverse to a stick, $$$\mathbf{\hat{g}\perp\hat{n}}$$$, is not suppressed: $$$\psi_\mathbf{\hat{n}\perp\hat{g}}$$$ does not decay at large $$$b$$$, equivalent to a negligible transverse diffusion coefficient $$$D_a^\perp$$$, and a negligible axonal radius compared to the free diffusion length. In contrast, the extra-axonal contribution $$$S^{\mathrm{eas}}(\mathbf{\hat{g}},\,b)$$$ coming from water diffusion in a simply-connected space characterized by a finite diffusion coefficient $$$D_e(\mathbf{\hat{g}})$$$ (with $$$D_e(\mathbf{\hat{g}})\geq D_e^\perp$$$), decays exponentially faster than the intra-axonal signal, by virtue of $$$e^{-bD_e^\perp}\ll 1$$$ for large enough $$$b$$$, and can be eventually neglected. Finally, $$$\gamma\equiv\,S|_{b=\infty}$$$ is the possible contribution of immobile (fully restricted) water11, which is shown to fall below our detection threshold.
Either a finite axonal radius, or a notable exchange rate between intra- and extra-axonal water, would destroy the $$$b^{-1/2}$$$ scaling, see Figure 3 where we investigate finite radius effects.
Fiber ODF quantification: We select voxels characterized by a single fiber population12 (SFP), and focus on the SFP-averaged signal $$$\tilde{S}_b(\theta)$$$ as a function of the angle $$$\theta$$$ between the gradient direction $$$\mathbf{\hat{g}}$$$ and the principal fiber direction $$$\mathbf{\hat{n}}_0$$$. We use the directional signal dependence of $$$\tilde{S}_b(\theta)$$$ in order to determine an SFP-averaged fiber ODF, and to obtain estimates of the intra-axonal diffusivity $$$D_a^\parallel$$$ and axonal dispersion. We prove that the orientational variance $$$\sigma_b^2$$$ of $$$\tilde{S}_b(\theta)$$$ approaches $$$\sigma_b^2\simeq\sigma^2\,+\frac1{2bD_a^\parallel}$$$. In Figure 4, we observe that this variance scales linearly with $$$1/b$$$ in all subjects. This scaling further allows us to determine both the intrinsic fiber orientational dispersion $$$\sigma$$$, and the intra-axonal diffusivity $$$D_a^\parallel$$$ separately from the axonal water fraction $$$f$$$.
Discussion and Conclusion
Our in vivo observation of the power-law exponent $$$\alpha\,=\,1/2$$$ provides direct evidence that axons can be represented as an array of zero-radius sticks, so that the diffusivity inside each stick transverse to its axis can be neglected. In biophysical terms, this picture reveals:
$$$\bullet$$$ long water residence time in axons, compared to typical diffusion times;
$$$\bullet$$$ the absence of a fully restricted isotropic diffusion compartment; and
$$$\bullet$$$ axonal radii do not exceed the shrinkage-corrected values obtained by histology13,14.
Acknowledgements
Financially supported by the Fellowship from Raymond and Beverly Sackler Laboratories for Convergence of Physical, Engineering and Biomedical Sciences, by the Litwin Foundation for Alzheimer’s Research, by the NIH/NINDS award R01NS088040, and by FWO fellowship 12S1615N.References
1. Yablonskiy and Sukstanskii (2010) NMR in Biomedicine 23:661-681
2. Kroenke et al. (2004) MRM 52: 1052-1059
3. Behrens et al. (2003) MRM 50: 1077-1088
4. Assaf et al. (2004) MRM 52: 965–978.
5. Jespersen et al. (2007) NeuroImage 34: 1473–1486
6. Callaghan et al. (1979) Biophys J 28: 133–141
7. Veraart et al. (2016) NeuroImage 142: 394-406
8. Kellner et al. (2016) MRM 76(5): 1574–1581
9. Gudbjartsson and Patz (1995) MRM 34(6): 910-914
10. Jensen et al. Neuroimage. 2015 Oct 1;124(Pt A):824-833
11. Stanisz et al. (1997) MRM 37(1): 103-111
12. Tax et a. (2013) Neuroimage 86:67-80
13. Aboitiz et al. (1992) Brain research 598:143– 153
14. Caminiti et al. (2009) PNAS 106, 19551–19556
15. Ronen et al. (2014) Brain Structure and Function 219:1773–1785
16. Leergaard et al. (2010) PloS one 5, e8595
Figures
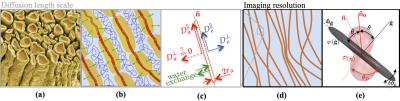
Figure 1: The existing conjecture presents water diffusion in WM (a, b) as restricted diffusion in an array of axons mimicked by sticks (red) embedded in the extra-axonal water (blue), whereas contribution of myelin (yellow) water is considered to be negligible. (c) Schematic representation for water diffusion properties of an individual stick. The diffusion length scale is at least two orders of magnitude smaller than the imaging resolution (d). Hence, the measured intra-axonal signal reflects the averaging over an ensemble of sticks, i.e. a convolution between axonal orientation distribution function and a stick response function, cf. first term of Eq.(2).
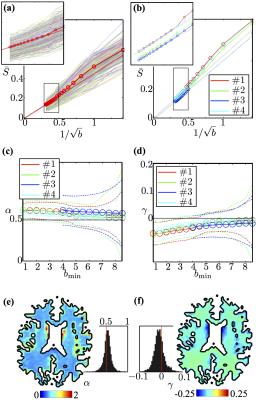
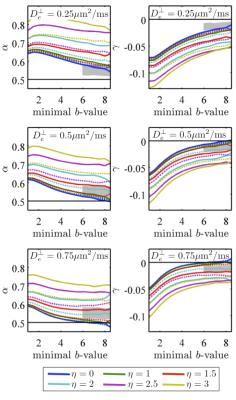
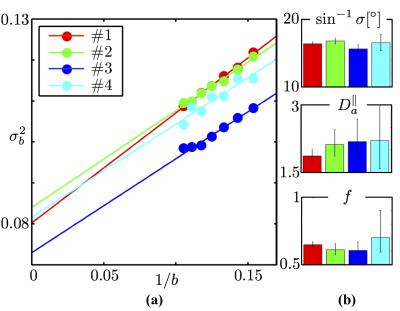
Figure 4: (a)$$$\,$$$ODF variance $$$\sigma_b^2$$$ at finite $$$b$$$, computed as the slope of $$$\ln\tilde{S}_b(\theta)$$$ vs $$$\cos^2(\theta)$$$, decays as $$$1/b$$$. (b)$$$\,$$$The intercept and slope of the variance as function of $$$1/b$$$ returns an in vivo estimate of the intrinsic axonal orientational dispersion $$$\sigma^2$$$ and intra-axonal diffusivity $$$D_a^\parallel\,=[1.9,\,2.2]\,\mathrm{\mu\,m^2\,/ms}$$$, respectively. The estimated dispersion angle $$$\sin^{-1}\sigma\approx\,17^\circ$$$ is in excellent agreement with histological studies yielding dispersion of about $$$18^\circ$$$15,16. Axonal water fraction $$$f$$$ is estimated using $$$D_a^\parallel$$$ and the parameter $$$\beta$$$, $$$f$$$ ranges between 0.6 and 0.7 amongst the four subjects. Error bars span the $$$95\%$$$ confidence interval; bar plots show reproducibility over 4 subjects.