0280
Validation of the two-pool diffusion model in post-mortem white matter using the CLARITY method1Max-Planck-Institute for Human Cognitive and Brain Sciences, Leipzig, Germany, 2Paul-Flechsig-Institute for Brain Research, Leipzig, Germany
Synopsis
Water diffusion in tissues is known to be non-Gaussian. Moreover, two different water regimes have been found in brain tissue and assigned to a bulk-like compartment and water in contact with macromolecules. Here, we investigate the influence of membranes in post-mortem white matter, which are assumed to be responsible for the second pool observed in MR-diffusion measurements. Using a newly developed CLARITY method, which removes lipids from brain tissue while keeping the brain structure intact, we found that the slow compartment vanished while the mobility of the fast pool increased, which directly demonstrates the influence of membranes on water dynamics.
Purpose
Water diffusivity in brain tissue is sensitive to the underlying microstructure but its biophysical basis is yet not completely understood. In previous MRI studies using high diffusion weightings, the signal attenuation was well described by a bi-exponential function, with two diffusion regimes of water assigned to a ‘fast’ bulk-like compartment and a ‘slow’ pool in contact with macromolecules.1
While water dynamics in brain tissue does not seem to be strongly affected by protein-based components like the extracellular matrix 2, it has been suggested that the slow pool primarily arises from water between myelin sheets in close contact to the lipid bilayers.3,4
To more directly assess the influence from myelin membranes on the MR-diffusion signal, we performed experiments in post-mortem white matter samples exposed to the CLARITY technique.5,6 This method removes lipid-based structures in the tissue, which are replaced by a hydrogel mesh linked to proteins and nucleic acids while the brain structure is kept intact.
Methods
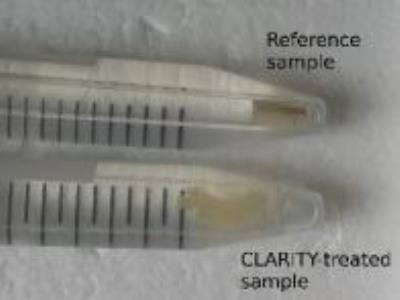
Two paraformaldehyde-fixed specimens from the same human corpus callosum were collected in $$$3\,\mathrm{mm}$$$-diameter glass tubes and stored in phosphate-buffered saline (PBS) solution at $$$4\,\mathrm{°C}$$$. One sample underwent CLARITY treatment while the other one served as a reference. In the first step, tissue is infiltrated with a hydrogel-monomer-formaldehyde solution. After crosslinking a tissue-hydrogel hybrid is created which is physically stable and preserves proteins and nucleic acids. In the second step, lipids are removed by incubation in an ionic sodium dodecyl sulfate (SDS) detergent. SDS micelles embrace lipid molecules and were extracted out of the tissue passively via diffusion and actively using electrophoresis. The CLARITY process is finished by an optical clearing in thiodiethanol. The result is a slightly transparent almost lipid-free tissue block (Figure 1).
Non-localized Stejskal-Tanner diffusion measurements were performed on a custom-built (3 T) FEGRIS NT spectrometer with a maximum gradient amplitude of $$$35000\,\mathrm{mT/m}$$$ along the main magnetic field.7 It permits to achieve very short diffusion times $$$(\Delta=2\,\mathrm{ms}; \delta=0.6\,\mathrm{ms}; T_E=4\,\mathrm{ms}; T_R=3\,\mathrm{s})$$$ to minimize restriction and compartmental exchange effects. The b-values were increased in 32 steps from $$$0.6$$$ to $$$20600\,\mathrm{s/mm}^2$$$, and the temperature was varied between $$$20$$$ and $$$0\,\mathrm{°C}$$$ in steps of $$$2\,\mathrm{°C}$$$. Additionally, $$$T_1$$$ and $$$T_2$$$ relaxation curves were measured with inversion-recovery and Carr-Purcell-Meiboom-Gill sequences, respectively. Diffusion and transverse relaxation data were fitted to a bi-exponential model, while mono-exponential fitting was used for $$$T_1$$$.
Results
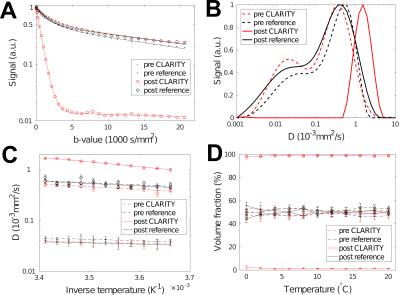
The signal attenuation at $$$20\,\mathrm{°C}$$$ and results from an inverse Laplace transform (ILT) of the data are shown in Figure 2 along with estimated diffusion coefficients and volume fractions. Before CLARITY treatment, both samples showed a clear deviation from mono-exponential behavior. Even at high b-values a significant echo could be recorded (Figure 3). The ILT indicated the presence of two compartments, which was verified by bi-exponential fitting. The estimated parameters at $$$20\,\mathrm{°C}$$$ were $$$D_f=5.5\cdot10^{-4}\,\mathrm{mm}^2\mathrm{/s}$$$ and $$$D_s=4.3\cdot10^{-5}\,\mathrm{mm}^2\mathrm{/s}$$$ for the fast and slow pools, respectively. The temperature dependencies of both coefficients followed an Arrhenius law with activation energies differing by roughly a factor of two. Both volume fractions were $$$\approx50\,\%$$$ and remained stable over the temperature range.
Upon CLARITY treatment, the signal decayed mono-exponentially with a diffusion coefficient, $$$D_{CLARITY}=1.65\cdot10^{-3}\,\mathrm{mm}^2\mathrm{/s}$$$, approaching that of bulk water ($$$D_{H_2O}=2.023\cdot10^{-3}\,\mathrm{mm}^2\mathrm{/s}$$$ ).9 That is, the diffusivity of the fast pool increased by a factor of three. The activation energy after CLARITY was $$$18.1\,\mathrm{kJ/mol}$$$, which is close to the value of bulk water ($$$18.8\,\mathrm{kJ/mol}$$$ ).9 A slower diffusion pool could not be reliably identified after lipid removal as indicated by the ILT result and the volume fraction of the fast pool approaching $$$100\,\%$$$.
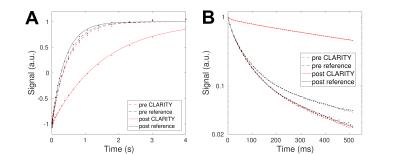
Figure 4 presents the results from $$$T_1$$$ and $$$T_2$$$ relaxation measurements at $$$20\,\mathrm{°C}$$$. After the clearing process, $$$T_1$$$ increased from $$$\approx500$$$ to $$$\approx1500\,\mathrm{ms}$$$ by a similar factor found for diffusion. Also the larger $$$T_2$$$ increased from $$$\approx50$$$ to $$$\approx100\,\mathrm{ms}$$$, while the short myelin water pool shrunk to less than $$$10\,\%$$$.
Discussion
The strong deviation from mono-exponential behavior despite ultra-short diffusion times of $$$2\,\mathrm{ms}$$$ in the native samples as well as the observation of two distinct signal fractions with activation energies differing by a factor of two is in line with previous reports and with the assumption of a two-pool diffusion model. The increase in water mobility after lipid removal indicates a strong interaction between water and membrane compounds. The slow diffusion/slow $$$T_2$$$ pool disappear upon CLARITY treatment, allowing to assign this fraction to water between myelin lamellae.Conclusion
Our observations indicate that the effect of non-Gaussian behavior in experiments employing high magnetic field gradients and short diffusion times is strongly affected by the existence of two separate water pools.Acknowledgements
This work was funded in part by the Helmholtz Alliance “ICEMED”.References
1. Le Bihan, D. The ‘wet mind’: Water and functional neuroimaging. Phys. Med. Biol. 2007; 52: R57-R90.
2. Georgi, J., Metere, R., Morawski, M., Jäger, C., Möller, H.E. Investigation of the influence of the extracellular matrix on water diffusion in brain and cartilage. Proc. Intl. Soc. Mag. Reson. Med. 2016 ; 24: 11.
3. Dhital, B., Labadie, C., Möller, H.E., Turner, R. Activation energies for water diffusion in ex-vivo white matter. Proc. Intl. Soc. Mag. Reson. Med. 2011; 19: 78.
4. Dhital, B., Labadie, C., Stallmach, F., Möller, H.E., Turner, R. Temperature dependence of water diffusion pools in brain white matter. NeuroImage. 2016; 127: 135–143.
5. Chung, K., Deisseroth, K. CLARITY for mapping the nervous system. Nature Meth. 2013; 10: 508-513.
6. Chung, K., et al. Structural and molecular interrogation of intact biological systems. Nature 2013; 497: 332-337.
7. Galvosas, P., Stallmach, F., Seiffert, G., Kärger, J., Kaess, U., Majer, G. Generation and application of ultra-high-intensity magnetic field gradient pulses for NMR spectroscopy. J. Magn. Reson. 2001; 151: 260–268.
8. Holz, M., Heil, S.R., Sacco, A. Temperature-dependent self-diffusion coefficients of water and six selected molecular liquids for calibration in accurate ¹H NMR PFG measurements. Phys. Chem. Chem. Phys. 2000; 2: 4740-4742.
9. Gillen, K., Douglass, D.C., Hoch, M.J.R. Self-diffusion in liquid water to −31 °C. J. Chem. Phys. 1972; 57: 5117-5119.
Figures