0279
Diffusion tensor distribution imaging1Department of Chemistry, Lund University, Lund, Sweden
Synopsis
Diffusion MRI is an excellent method for detecting subtle changes of brain microstructure, but rarely gives unambiguous information about whether the observations originate from variations in cell density, size, shape, orientation, or any combination thereof. Capitalizing on our recent pulse sequences with data acquisition as a function of both the spherical and the conventional linear components of the diffusion encoding tensor b, we here introduce and demonstrate a method to quantify the composition of a heterogeneous voxel as a multidimensional distribution of diffusion tensors where the information about size, shape, and orientation is cleanly separated in the respective dimensions of the distribution. When transferred to a neuroimaging context, our method will allow for unconstrained estimation of fiber bundle orientation distributions and radial and axial diffusivities, as well as fractions of extracellular water and cerebrospinal fluid.
Purpose
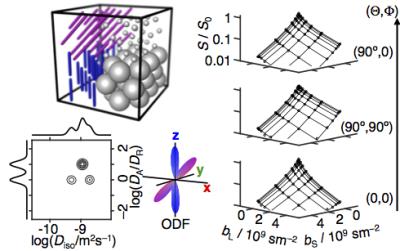
The parameters measured with conventional diffusion MRI depend on microstructural properties such as cell density, size, shape, and orientation. While the conventional parameters sensitively report on changes in any of these properties, they rarely give unambiguous information about which one of them has changed. As an example, estimation of nerve fiber orientation distributions rely on the unverified assumption that the diffusion properties of the individual fibers are identical for all voxels being compared,1 and is consequently confounded by changes in any of the other cellular properties. As a solution to this problem, we here introduce a method for quantifying the microstructure of a heterogeneous voxel as a diffusion tensor distribution (DTD) that we estimate without any priors or constraints on the number of components or their individual properties (see Fig 1).Theory
The signal S(b) from an ensemble of microscopic diffusion tensors D is given by
S(b) = S0<exp(-b:D)>
where b is the b-tensor, S0 is the initial signal, <> denotes an ensemble average, and b:D is a generalized scalar product. The tensor D is parameterized with its isotropic average ("size") Diso, ratio between axial and radial diffusivities ("shape") DA/DR, and orientation (θ,φ).2 We have recently introduced spherical diffusion encoding bS as an additional acquisition dimension to be used in conjunction with conventional linear encoding bL in the direction (Θ,Φ).3,4 The tensor b is then parameterized with (bS,bL,Θ,Φ),5 and the multidimensional signal S(bS,bL,Θ,Φ) can be written as an integral transformation from the continuous DTD P(Diso,DA/DR,θ,φ) with the kernel K(bS,bL,Θ,Φ,Diso,DA/DR,θ,φ). In Ref. 5 we showed that the size-shape projection P(Diso,DA/DR) can be estimated from orientationally averaged data S(bS,bL) by numerical inversion of the integral transformation. As illustrated in Fig 1, we here extend our previous approach by including the orientational information, thereby obtaining the full size-shape-orientation DTD.
Experiments
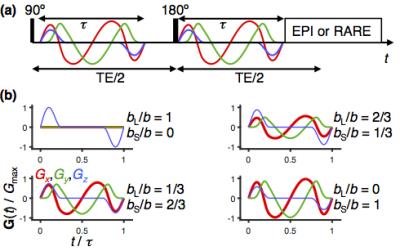
Proof-of-principle experiments were performed on a composite phantom constructed from a 5 mm glass tube with a reverse hexagonal liquid crystal (linear diffusion tensors with random orientations)2,5,6 inside a 10 mm glass tube with an aqueous polymer solution (two isotropic components). Data was acquired on a Bruker 11.7 T microimaging system with the pulse sequence in Fig 2 using single-shot RARE read-out at 0.6×0.6 mm in-plane spatial resolution, 16×16 matrix size, 1 mm slice thickness, for an array of 480 values of (bS,bL,Θ,Φ) generated by smoothly modulated gradients.4,6 After standard image reconstruction, P(Diso,DA/DR,θ,φ) was estimated for each voxel by numerical inversion of the S(bS,bL,Θ,Φ) data using in-house Matlab code.5
Results and Discussion
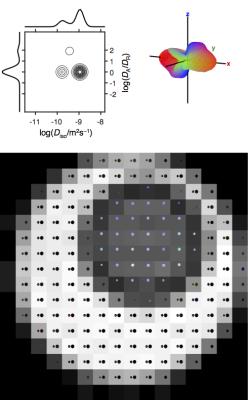
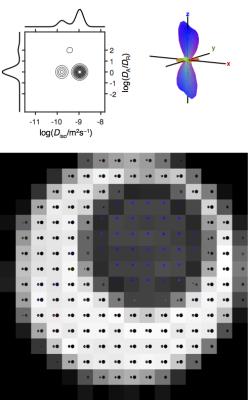
The experimental data in Fig 3 and 4 verifies that our new approach correctly identifies voxels with two distinct values of Diso, as well as both orientationally disordered and ordered anisotropic diffusion. By adding a dimension with spherical diffusion encoding to an otherwise rather standard data set with multiple b-values in different directions, the data contains sufficient information to allow unconstrained inversion into DTDs, which is in stark contrast to all other methods available today. For the data in Fig 3, conventional DTI and DKI would report low anisotropy and high kurtosis without being able to resolve the fundamentally different microstructures. In fact, all DTI and DKI parameters can be calculated by mixing various means and variances of the "pure" size, shape, and orientation dimensions of the DTD.8
The acquisition protocol is closely related to free gradient waveforms giving isotropic diffusion encoding as demonstrated in recent in vivo studies.7-9 In these studies, the results were reported in terms of the scalar parameters introduced in Ref 4, quantifying the spread of isotropic diffusivities, the mean-square anisotropy, and the orientational order, which through detailed comparison with quantitative microscopy have been shown to directly correspond to variability in cell density and average cell eccentricity.8
Conclusion
We have introduced and demonstrated an acquisition protocol and data inversion algorithm allowing for detailed characterization of heterogeneous voxels as DTDs with size, shape, and orientation dimensions. The results from the present study of well-defined phantoms show that there is potential for extracting even more detailed information from data acquired with combinations of spherical and linear diffusion encoding using the pulse sequence introduced in Ref 4 and recently applied in vivo.7-9 DTDs mapped on a voxel-by-voxel basis, as in Fig 3 and 4, will permit mapping of fiber orientation distributions, axial and radial diffusivities of distinct fiber populations, and fraction of cerebrospinal fluid, using only a minimum of modelling assumptions.
Acknowledgements
This work was financially supported by the Swedish Foundation for Strategic Research (AM13-0090) and the Swedish Research Council (2014-3910).References
1. Tournier JD, Calamante F, Gadian DG, Connelly A. Direct estimation of the fiber orientation density function from diffusion-weighted MRI data using spherical deconvolution. Neuroimage 2004;23:1176-1185.
2. Eriksson S, Lasic S, Nilsson M, Westin C-F, Topgaard D. NMR diffusion encoding with axial symmetry and variable anisotropy: Distinguishing between prolate and oblate microscopic diffusion tensors with unknown orientation distribution. J Chem Phys 2015;142:104201.
3. Eriksson S, Lasic S, Topgaard D. Isotropic diffusion weighting by magic-angle spinning of the q-vector in PGSE NMR. J Magn Reson 2013;226:13-18.
4. Lasic S, Szczepankiewicz F, Eriksson S, Nilsson M, Topgaard D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Front Physics 2014;2:11.
5. de Almeida Martins JP, Topgaard D. Two-dimensional correlation of isotropic and directional diffusion using NMR. Phys Rev Lett 2016;116:087601.
6. Topgaard D. Director orientations in lyotropic liquid crystals: Diffusion MRI mapping of the Saupe order tensor. Phys Chem Chem Phys 2016;18:8545-8553.
7. Szczepankiewicz F, Lasic S, van Westen D, Sundgren PC, Englund E, Westin C-F, Ståhlberg F, Lätt J, Topgaard D, Nilsson M. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors. Neuroimage 2015;104:241-252.
8. Westin C-F, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, Mattisson C, Bogren M, O'Donnell L, Kubicki M, Topgaard D, Nilsson M. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage 2016;135:345-362.
9. Szczepankiewicz F, van Westen D, Englund E, Westin C-F, Ståhlberg F, Lätt J, Sundgren PC, Nilsson M. The link between diffusion MRI and tumor heterogeneity: Mapping cell eccentricity and density by diffusional variance decomposition (DIVIDE). Neuroimage Accepted.
Figures