Synopsis

Time dependence of microscopic anisotropy measured with diffusion MRI can reveal the cellular eccentricity at different lengths scales, which is an important step towards the goal of non-invasive characterization of tissue microstructure. Diffusion sequences which vary the gradient orientation within one measurement can probe microscopic anisotropy, regardless of the macroscopic tissue configuration. Here we employ the newly proposed Double Oscillating Diffusion Encoding (DODE) sequences, consisting of two independent trains of oscillating gradients which can have different orientations, in order to measure the time dependence of microscopic anisotropy in the mouse brain.

Purpose

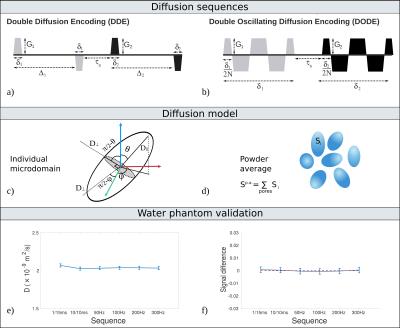
Estimating microscopic anisotropy (μA), which reflects microscopic-scale pore eccentricity, is an important objective of many diffusion MRI studies aiming to characterize tissue microstructure. An established technique for measuring μA consists of double diffusion encoding (DDE) sequences^1-5, usually acquired with fixed timing parameters. Investigating the time/frequency dependence of μA can potentially provide richer information by probing different restriction scales. Double oscillating diffusion encoding (DODE)⁶ sequences, which replace the two pairs of pulsed gradients in a conventional DDE with trains of oscillating gradients (Fig.1b), can measure the frequency dependence of μA.

Here, we implement DODE and DDE sequences on an ultra-high field pre-clinical scanner, derive a time-dependent metric of μA for DODE sequences, and investigate the unexplored time-dependence of microscopic anisotropy in the mouse brain.

Theory

Diffusion signal:

Microscopic anisotropy measured with DDE can be characterised using the fractional eccentricity metric⁷:

$$FE_{DDE}^2=\frac{\epsilon}{\epsilon+(3\Delta^2/5)(\text{Tr}D/3)^2},~\text{where}~\epsilon q^4=\log{\left(\frac{1}{12}\sum S_\parallel\right)}-\log{\left(\frac{1}{60}\sum S_\perp\right)},~\text{with}~q=\gamma G\delta~(1)$$

For DODE sequences we adapt the derivation in [8,9]. The powder averaged signal, computed over randomly oriented microdomains with frequency dependent parallel and perpendicular diffusivities ($$$D(ω)_\parallel$$$ and $$$D(ω)_\perp$$$), has the following expressions for DODE sequences with parallel and perpendicular gradients:

$$S_\parallel^{p.a.}=\frac{1}{2}\int_0^\pi\exp{\left[-(b_1+b_2)(D(\omega)_\parallel\cos^2\theta+D(\omega)_\perp\sin^2\theta)\right]\sin\theta d\theta}~(2)$$ $$S_\perp^{p.a.}=\frac{1}{4\pi}\int_0^{2\pi}\int_0^{\pi}\exp{\left[-b_1\left(D(\omega)_\parallel\cos^2\theta+D(\omega)_\perp\sin^2\theta\right)\\-b_2\left(D(\omega)_\parallel\sin^2\theta\cos^2\phi+D(\omega)_\perp\sin^2\phi+D(\omega)_\perp\cos^2\theta\cos^2\phi\right)\right]\sin\theta d\theta d\phi}~(3)$$

where b₁ and b₂ are the b-values of the two gradients, and angles θ and φ define the gradient directions relative to each microdomain (Fig.1c). Calculating the cummulant expansion up to second order in b, the difference between DODE sequences with parallel and perpendicular gradients when b₁=b₂ is: $$\log{\left(S_\parallel^{p.a.}\right)}-\log{\left(S_\perp^{p.a.}\right)}=b^2\frac{2}{15}\left(D(\omega)_\parallel-D(\omega)_\perp\right)^2~(4)$$

The powder averaged signal is equivalent to the mean signals in equation (1)⁸. Thus, FE_DODE is computed as:

$$FE_{DODE}^2=\frac{\frac{2}{15}\left(D(\omega)_\parallel-D(\omega)_\perp\right)^2}{\frac{2}{15}\left(D(\omega)_\parallel-D(\omega)_\perp\right)^2+\frac{3}{5}(\text{Tr}D/3)^2}=\frac{2}{3}\cdot\frac{\left(D(\omega)_\parallel-D(\omega)_\perp\right)^2}{D(\omega)_\parallel^2+2D(\omega)_\perp^2},~(5)$$

and is equivalent to the fractional anisotropy of each microdomain⁵.

Methods

All experiments have been performed on a 16.4T Bruker Ascend Aeon scanner equipped with a Micro5 imaging probe capable of producing up to 3000mT/m in all three directions.

Phantom validation: First, we used a water phantom to test the implementation of DODE and DDE sequences and their b-value calculation.

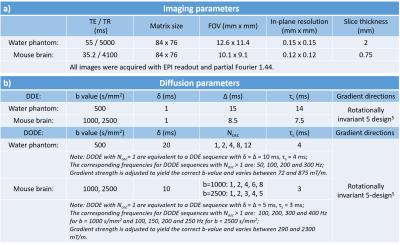
Brain imaging: All experiments were preapproved by the Institution’s animal ethics committee. The brains were perfused from healthy mice (M=4), immersed in gadoterate meglumine 2.5mM for 24h before scanning and kept at 37^oC during scans. Acquisition parameters are detailed in Table 1.

Data analysis: MR datasets were denoised using MRtrix3^11,12 and analysed in Matlab. We investigate the time dependence of mean diffusivity (MD) and fractional anisotropy (FA) (measured at b=1000s/mm² from sequences with parallel gradients) as well as fractional eccentricity (FE) (measured at both b=1000 and 2500s/mm² using the entire protocol) in the whole brain and in various white and gray matter ROIs.

Results

Phantom validation:

The results illustrated in Fig.1e)-f) confirm the solid performance of DODE and DDE MRI sequences. The estimated diffusivity values are between 2.03 and 2.07 x10^-9m²/s for all sequences (Fig.1e), which corresponds to the values for water at 22^oC. The signal difference between measurements with parallel and perpendicular gradients is indistinguishable from zero (Fig.1f), as expected for water.

Brain imaging:

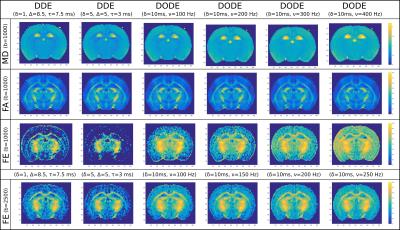
Parameter maps illustrating the time-dependence of various metrics (MD, FA and FE) measured with DDE and DODE sequences with different frequencies are shown in Fig.2. The results show that MD increases with frequency, while FA is fairly constant. FE values show pronounced increase with frequency, especially in gray matter. The results are consistent for all subjects.

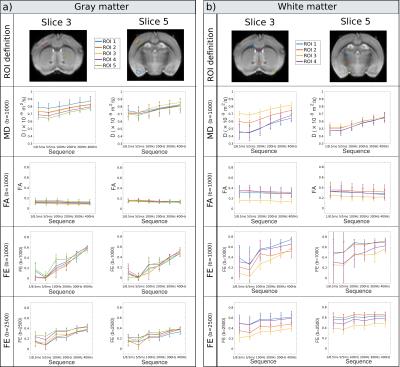
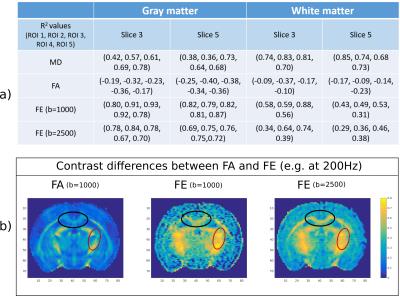
A quantitative analysis of parameter time-dependence in various GM and WM ROIs is presented in Fig.3. The mean parameter values are calculated across all subjects and all ROI voxels. The results show that MD increases with frequency in both WM (0.66<R²<0.85) and GM (0.36<R²<0.78), while FA slightly decreases (WM: -0.09>R²>-0.37; GM: -0.17>R²>-0.39). FE values increase with frequency in all ROIs (WM: 0.28<R²<0.87; GM: 0.70<R²<0.93), nevertheless, the increase is more pronounced in GM. In general FE is higher than FA as it directly reflects the microscopic anisotropy of tissue without the effect of fibre orientation, which decreases FA in areas of crossing/fanning fibres (Fig.4b).

Discussion

Acknowledgements

References

¹ P. P. Mitra. Multiple wave-vector extensions of the NMR pulsed-field-gradient spin-echo diffusion measurement. Physical Review B, 51(21):15074–15078., 1995.

² Y. Cheng and D. Cory. Multiple scattering by NMR. J. Am. Chem. Soc, 121:7935–7396, 1999

³ N. Shemesh, E. Özarslan, T. Adiri, P. J. Basser, and Y. Cohen. Noninvasive bipolar double-pulsed-field-gradient NMR reveals signatures for pore size and shape in polydisperse, randomly oriented, inhomogeneous porous media. Journal of Chemical Physics, 133:044705, 2010.

⁴ N. Shemesh and Y. Cohen. Microscopic and compartment shape anisotropies in grey andwhite matter revealed by angular bipolar double-PFG. Magnetic Resonance in Medicine, 65:1216–1227, 2011 5M.

⁵ Lawrenz and J. Finsterbusch. Mapping measures of microscopic diffusion anisotropy in human brain white matter in vivo with double-wave-vector diffusion-weighted imaging. Magnetic Resonance in Medicine, 73(2):773-83, 2015

⁶ A. Ianus, N. Shemesh, D. C. Alexander, and I. Drobnjak. Double oscillating diffusion encod-ing and sensitivity to microscopic anisotropy. Magnetic Resonance in Medicine, Early View, 2016.

⁷ S. N. Jespersen, H. Lundell, C. K. Sonderby, and T. B. Dyrby. Orientationally invariant metricsof apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR in Biomedicine, 26:1647–1662, 2013, and its erratum.

⁸ P. T. Callaghan, K. W. Jolley, and J. Lelievre. Diffusion of water in the endosperm tissue of wheat grains as studied by pulsed field gradient nuclear magnetic resonance. Biophysical Journal, 28:133–141, 1979.

⁹ D. Topgaard and O. Söderman. Self-diffusion in two- and three-dimensional powders of anisotropic domains: An NMR study of the diffusion of water in cellulose and starch. The Journal of Physical Chemistry, 106:11887 – 92, 2002.

¹⁰ E. Kaden, N. D. Kruggel, and D. C. Alexander.Quantitative mapping of per-axon diffusion coefficients in brain white matter. Magnetic Resonance in Medicine, 75:1752-63,2015.

¹¹ J. Veraart, D.S. Novikov, D. Christiaens, B. Ades-aron, J. Sijbers, and E. Fieremans. Denoising of diffusion MRI using random matrix theory. NeuroImage, 2016, in press,

¹² J. Veraart, E. Fieremans, and D. S. Novikov, Diffusion MRI noise mapping using random matrix theory. Magn. Res. Med., 2016, early view

¹³ S. N. Jespersen, B. Hansen, E. Stubbe, D. Nunes and N. Shemesh, Fast kurtosis imaging and its application to assess time dependence of diffusion and kurtosis parameters in the rat spinal cord. Front. Phys. Conference Abstract: New dimensions in diffusion encoding. 2016