0251

Population Receptive Field Mapping of Human Somatosensory Cortex at 7 T
Michael Asghar1, Rosa Sanchez-Panchuelo1, Denis Schluppeck2, and Susan Francis1

1SPMIC, School of Physics, University of Nottingham, Nottingham, United Kingdom, 2School of Psychology, University of Nottingham, Nottingham, United Kingdom

Synopsis

To advance the investigation of function and structure in human somatosensory areas, detailed topographic maps that are reproducible across time are invaluable. In previous 7 Tesla fMRI studies using travelling wave (TW) and event-related (ER) paradigms, the functional parcellation of digit representations in human S1 has been shown. Here, we present the application of ‘population Receptive Field’ analysis (pRF) to high-resolution fMRI data from somatosensory cortex. The pRF method can provide information beyond preferred stimulus location, such as measures of receptive field size. We also show how surface coils can be used to improve spatial resolution in somatotopic maps.

Purpose

Detailed and reproducible topographic maps are important for studying somatosensory cortex (S1/S2) in healthy individuals and patients, e.g. altered sensory hand representations in dystonia. However, underlying mechanisms are unclear and detailed maps of such changes are unavailable1. Until now, block2,3, travelling wave (TW) and event-related (ER) paradigms4,5 have been used to measure somatotopic maps in human S1. Here, we apply population Receptive Field (pRF) mapping6 to 7T functional MRI data of S1, providing additional information (pRF size, preferred stimulus location) about the functional organization of S1.

Methods

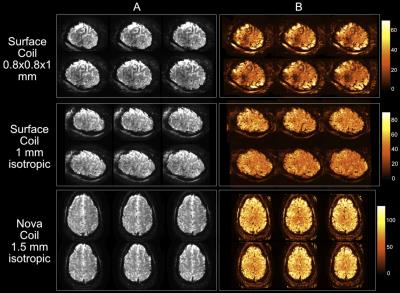
Somatosensory fMRI data were collected on a 7T Philips Achieva scanner using either (1) a 32-channel Nova receive coil (four datasets, two at MB2) and (2) two 16-channel surface coils (MRCoils) (three datasets, MB1). fMRI parameters: GE-EPI BOLD, TR/TE = 2000/25ms; 32-ch Nova Coil: (1.5mm)3 (MB2) & (1.25mm)3 (MB1), 26/52 slices; 32-ch Surface coil: 0.8×0.8×1mm3 & 1mm3 (MB1), 20 slices. High-resolution structural data: T1-weighted, Phase Sensitive Inversion Recovery (PSIR) images, 0.3×0.3×1mm3.

The fMRI paradigm used nine independently controlled piezo-devices (Dancer Design, UK) to deliver vibrotactile stimuli (30 Hz) to each phalanx of the index (D2), middle (D3), and ring finger (D4) of subjects’ right hand, in a 3×3 grid of stimulation sites. Each piezo-device stimulated ~1mm2 of skin. The paradigm comprised a modified TW paradigm interspersed with brief rest periods: (a) between digits (BD), 6s stimuli per digit, 12 cycles, (b) within-digits (WD), 6s stimuli on proximal to distal sites, 12 cycles, (c) diagonal stimulation (Diag), 6s, 8 cycles.

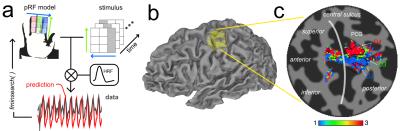
To fit the somatosensory fMRI data, we adapted a previously reported pRF framework6. We tested different models for the spatial layout of the pRF (1-dimensional/2D-Gaussian, unconstrained) and haemodynamic response function (single, double-gamma), to compute predicted fMRI responses from the spatial location of the stimuli (3×3 grid) over time. The best-fit parameters were estimated by nonlinear least squares7,8. fMRI data were also analyzed using Fourier-based TW methods to produce comparison somatotopic maps. For visualization, parameter maps from the pRF and TW analyses were superimposed on cortical surfaces derived using FreeSurfer9,10.

Results

Temporal signal-to-noise (tSNR) calculations confirmed the benefits of the surface coil: 1.4x reduction in tSNR despite a 5x volume reduction (Fig.1, 2), yielding increased number of voxels for analysis.

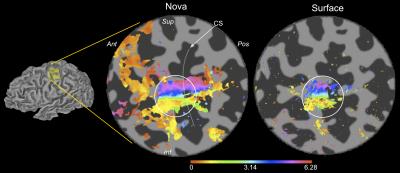
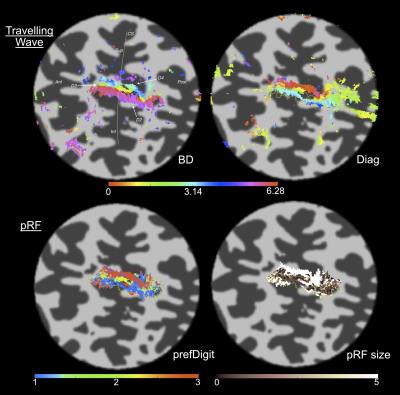
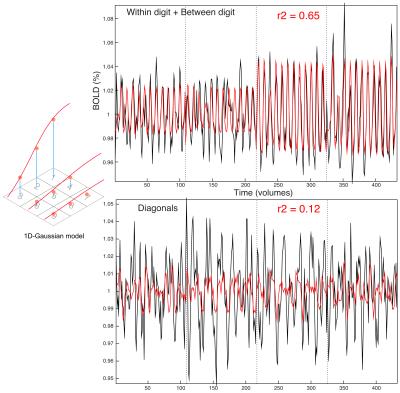
Across datasets, the 1D Gaussian pRF model (Fig.3) provided the best fit to the data (r2 up to 0.65, per voxel). This parametrization of the pRF shape assumes a 1D-Gaussian profile along the proximal-distal axis of each digit. This model provided a good fit to data for BD and WD stimulation, corresponding to the “major” axes of the maps in S1. Somatotopic pRF maps of ‘preferred digit’ and ‘preferred proximal/distal location’ were consistent with TW analysis (Fig.4).

Surprisingly, model fits for diagonal stimulation were poor, suggesting these complex spatial response patterns led to interactions uncaptured by our pRF model (Fig.5). By considering the “diagonal” map as a weighted linear combination of BD and WD maps, residuals between the data and the best fitting least squares estimate can provide information regarding interaction effects.

Discussion

pRF mapping is an increasingly popular fMRI analysis method, particularly in visual cortex11.

The best fit parameters (minimizing the squared error between a voxel’s timecourse and predicted fMRI timeseries), provide information about neuronal ensembles that contribute to the voxel fMRI response. Here, we show that pRF analysis can be extended to high-resolution S1 data. pRF somatotopic map quality (preferred stimulus location) was comparable to TW (Fourier-based) maps (Fig.4). However, pRF maps provide additional pRF size information. Our results also show that using a surface coil capitalises on higher field strength12,13 by increasing TW map spatial resolution (Fig.2).

We have two challenges: 1) increasing the sampling of sensory space beyond our 3x3 grid and 2) identifying a physiologically relevant pRF model parameterization. We assume that voxel responses are an additive combination of the responses to each stimulation site; the poorly model-fitted diagonal stimulation data suggest that this assumption is violated.

We are now moving to a finer stimulation grid (4x4), and extending the pRF model to account for apparent nonlinear effects, which may be due to interactions in stimuli space, the cortex or across time (trial history).

Conclusion

We show pilot data confirming the pRF method in somatosensory cortex at 7T fMRI, with pRF mapping providing additional information, such as pRF size, compared to TW experiments. The development of software (more complex pRF models) and hardware (finer sampling of sensory space, surface coil) are key steps towards higher quality cortical mapping.

Acknowledgements

This work was funded by an MRC grant (MR/M022722/1).

References

1. Butterworth, S. et al. Movement Disorders. 2003;18(6):673-682.

2. Stringer, EA, et al. NeuroImage. 2011;54:1012-1020.

3. Martuzzi, R, et al. Human Brain Mapping. 2014;35:213-226.

4. Sanchez-Panchuelo RM, et al. Neuroimage. 2014;93:221-230.

5. Sanchez-Panchuelo RM, et al. J Neurophysiol. 2010;103:2544-2556.

6. Dumoulin S, et al. Neuroimage. 2008;39:647-660.

7. Nelder JA, et al. The Computer Journal. 1965;308-313.

8. Marquardt DW, JSTOR. 1963;11(2):431-441.

9. Dale, AM, et al. NeuroImage. 1999;9:179-194.

10. Fischl B, et al. NeuroImage. 1999;9:195-207.

11. Wandell BA, et al. Brain Mapping: An Encyclopedic Reference. 2015;1:651-659.

12. Yacoub E, et al. Magnetic Resonance in Medicine. 2001;45:588-594.

13. Francis S, et al. Physiol. Meas. 2014;35:R167-R185.

Figures

Figure1: A) Mean (grey) and B) temporal signal-to-noise ratio (tSNR, hot) images comparing surface coil and Nova coil EPI data. Images shown for three spatial resolutions, and all images acquired at MB1. tSNR values are based on the first 20 dynamics of a scan. The tSNR values are 1.4x lower using the surface coil, but the spatial resolution is improved by a factor of 5 (0.64 mm3 versus 3.375 mm3). tSNR values in a somatosensory ROI were averaged over multiple scans: (~65, Nova, ~45, Surface).

Figure2: A comparison of Nova coil TW data to surface coil TW data, in the same subject, over different scan sessions. The functional data are displayed on flattened cortices; a mid-grey matter surface is shown for visual comparison. The TW paradigm involved fingertip stimulation of all 5 digits as described in a previous publication1. Nova data is acquired at (1.5 mm)3 and surface coil acquired at 0.8x0.8x1 mm3. The surface coil provides a greater number of voxels, providing justification for performing pRF mapping.

Figure3: a) Somatosensory pRF model fitting procedure: the pRF model is combined with the stimulus description to obtain the predicted pRF response which is finally convolved with an HRF. Best fit estimates for each voxel’s fMRI timeseries are obtained using nonlinear least squares (Nelder-Mead or Levenberg-Marquardt); b) S1 ROI on left hemisphere (mid grey matter surface); c) Preferred digit parameter map indicating D2 (blue), D3 (green), & D4 (red), for one subject.

Figure4: A comparison of travelling wave (Fourier analyses) and pRF data in one subject. The data were collected using a Nova coil (MB1), using a 3 digit paradigm described in the text, and overlaid on a flattened cortex. The pRF provides comparable estimates of preferred digit to travelling wave analysis, as well as providing information such as pRF size.

Figure5: Model fitting comparison. The 1D-Gaussian pRF model was fitted separately to a concatenated within digit & between digit (4 runs) scan and a diagonal (4 runs) scan. The data were acquired on a Nova coil (MB2). The model fits well to within and between digit (r2 = 0.65), but surprisingly poorly to diagonal stimulation data (0.12) – per best fitting voxel.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)
0251