0209

A Robust Reconstruction Method for Quantitative Perfusion MRI: Application to Brain Dynamic Susceptibility Contrast (DSC) Imaging

Cagdas Ulas^1,2, Pedro A. Gomez^1,2, Jonathan I. Sperl², Christine Preibisch³, Marion I. Menzel², Axel Haase⁴, and Bjoern H. Menze¹

¹Department of Computer Science, Technische Universität München, Munich, Germany, ²GE Global Research, Munich, Germany, ³Department of Neuroradiology, Technische Universität München, Munich, Germany, ⁴Zentralinstitut für Medizintechnik, Technische Universität München, Munich, Germany

Synopsis

We propose a robust reconstruction model for dynamic perfusion magnetic resonance imaging (MRI) from undersampled k-space data. Our method is based on a joint penalization of the pixel-wise incoherence on temporal differences and patch-wise dissimilarities between spatio-temporal neighborhoods of perfusion image series. We evaluate our method on dynamic susceptibility contrast (DSC)–MRI brain perfusion datasets and demonstrate that the proposed reconstruction model can achieve up to 8-fold acceleration by yielding improved spatial reconstructions and providing highly accurate matching of perfusion time-intensity curves, thus leading to more precise quantification of clinically relevant perfusion parameters over two existing reconstruction methods.

Purpose

Perfusion-weighted MR imaging (PWI) is a widely used imaging technique that allows to measure the hemodynamic parameters of perfusion through the examination of spatio-temporal changes of signal intensities following the injection of bolus via exogenous contrast agents. Although PWI techniques have become widespread clinical tools for the assessment of tumor malignancy, quantitative PWI requires high temporal resolution to capture the rapid kinetics of contrast agent uptake, high spatial resolution to accurately delineate spatial boundaries, and high signal-to-noise ratio to enable precise fitting of quantitative model parameters¹. With such severe limitations, quantitative PWI can greatly benefit from dynamic imaging reconstruction techniques^2,3,4. This work presents a new reconstruction model that is specifically developed for PWI and is capable of producing high-quality spatial images and reconstructing the complete temporal signal dynamics, hence enabling accurate estimation of perfusion parameters from accelerated acquisitions.

Methods

Our reconstruction model integrates two different data-driven constraints for the reconstruction of PWI: (i) the pixel-wise sparsity constraint on the temporal differences of the image series, limiting the overall dynamic of the perfusion time series, (ii) the patch-wise similarity constraint on the spatio-temporal neighborhoods of the whole data, providing smooth image regions with less temporal blurring when there are high inter-frame intensity changes. The proposed model can be formulated as, $$\hat{X}=\underset{X}{\arg\min}\left\lbrace\frac{1}{2}\|\mathcal{F}_uX-Y\|_2^2+\lambda_1\mathcal{G}_1(X)+\lambda_2\mathcal{G}_2(X)\right\rbrace$$ where $$$X$$$ denotes the perfusion image series to be reconstructed, $$$Y$$$ represents undersampled k-space data, $$$\lambda_1$$$ and $$$\lambda_2$$$ are the regularization parameters. The first regularizer here penalizes the sum of pixel-wise differences on the temporal difference images based on a reference, and defined as, $$\mathcal{G}_1(X)=\sum\limits_{t\in\mathbb{T}}\sum\limits_{n=1}^{M\times N}\sqrt{\left(\nabla_x\left(x_t-\bar{x}\right)_n\right)^2+\left(\nabla_y\left(x_t-\bar{x}\right)_n\right)^2}$$where $$$\bar{x}$$$ is a reference image calculated by averaging all temporal frames, $$$\nabla_x$$$ and $$$\nabla_y$$$ are the finite-difference operators along $$$x$$$ and $$$y$$$ dimensions, respectively. This regularizer is better adjusted to the variation in time. The second regularizer penalizes the weighted sum of $$$\ell_2$$$ norm distances between spatio-temporal (3D) patches of the image series, and this term is specified by,$$\mathcal{G}_2(X)=\sum_{(\mathrm{p}_x,\mathrm{p}_y,\mathrm{p}_t)\in\mathrm{\Omega}}\sum_{(\mathrm{q}_x,\mathrm{q}_y,\mathrm{q}_t)\in\mathcal{N}_{\mathrm{p}}}w(\mathrm{p},\mathrm{q})\|P_{\mathrm{p}}(\mathrm{X}^{3D})-P_{\mathrm{q}}(\mathrm{X}^{3D})\|_2^2$$ where $$$P_{\mathrm{p}}(\mathrm{X}^{3D})$$$ is a 3D patch centered at voxel $$$\mathrm{p}$$$, $$$\mathcal{N}_{\mathrm{p}}$$$ is a 3D search window around $$$\mathrm{p}$$$. The weights $$$w(\mathrm{p},\mathrm{q})$$$ are determined using exponentially weighted $$$\ell_2$$$ norm distance. This regularizer can exploit similarities between patch pairs and enforce smooth solutions by averaging distance-wise close patches.

To efficiently solve the optimization, we adopt an accelerated iterative algorithm based on a generalized forward-backward splitting framework⁵. We evaluate our method using five DSC image series acquired within a PET/MR study on brain tumor hypoxia. Data were acquired using a 3T Siemens mMR Biograph scanner with a 2D dynamic single-shot gradient-echo EPI sequence (TR/TE=1500/30 ms, flip angle=70$$$^{\circ}$$$, voxel size=$$$1.8\times1.8\times4$$$ mm$$$^3$$$, 60 dynamics). A bolus of 15 ml Gd-DTPA (Magnevist, 0.5 mmol/ml) was injected 3 minutes after an initial bolus of 7.5 ml with 4 ml/s injection rate. We compare our method with two reconstruction methods: SparseSENSE with multiple constraints⁶ and k-t RPCA^7. For fair comparison, we empirically fine-tuned the optimal regularization parameters for each method. Undersampling was retrospectively done via variable density Poisson-disc sampling⁸. Concordance correlation coefficients (CCCs) are used to quantitatively compare the perfusion maps.

Results

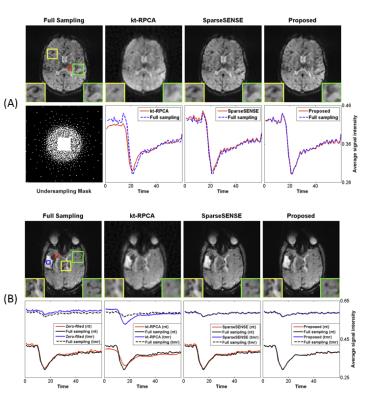
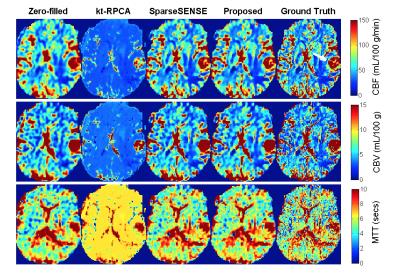
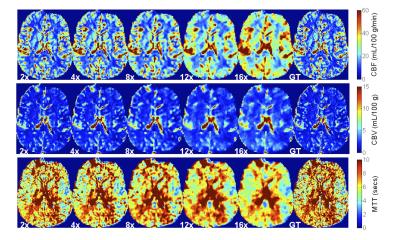
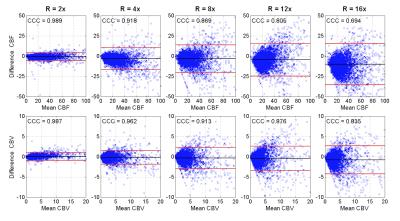
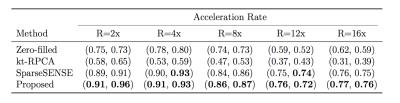
Figure 1 displays the results of both spatial reconstructions and estimated perfusion time-intensity curves of all methods obtained from two different subjects with an 8-fold acceleration. The proposed method yields the most accurate matching of peaks and temporal pattern of perfusion signal and produces acceptable spatial reconstructions together with SparseSENSE. Figure 2 demonstrates resulting perfusion maps of different reconstruction methods with 8-fold acceleration. Our method produces maps that are closer to the GT maps obtained by fully sampled data and provide sharper edges compared to SparseSENSE. The inefficiency of kt-RPCA for quantitative PWI is also demonstrated in Figure 2. Figure 3 shows how the quality of perfusion maps of a subject decreases depending on increasing acceleration rates, and this evidence is quantitatively assessed and illustrated for another subject in Figure 4. Table 1 reports the average CCCs of CBF and CBV parameters obtained from all methods with increasing acceleration rates. Our method yields the best CCCs up to 8-fold acceleration and shows similar performance like SparseSENSE at further accelerations.

Discussion

This study presents an efficient reconstruction method for quantitative PWI, which jointly exploits the temporal variations in pixel-wise and patch-wise level. The processing time of our method on a single-slice DSC-MRI dataset is around 4-5 minutes (on a Intel desktop). The maximum acceleration achieved with our method could be further increased with the use of a high-spatial resolution data. However, high-spatial resolution is not clinically realistic for PWI because a high temporal resolution is necessary to accurately track the kinetics of the tracer.

Acknowledgements

The research leading to these results has received funding from the European Union’s H2020 Framework Programme (H2020-MSCA-ITN-2014) under grant agreement no 642685 MacSeNet.

References

1. Smith, D.S. et al. Robustness of quantitative compressive sensing MRI: the effect of random undersampling patterns on derived parameters for DCE- and DSC-MRI. IEEE Trans. Med. Imag. (2012).

2. Lingala, S.G. et al. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans. Med. Imag. (2011).

3. Chen, C. et al. Real time dynamic MRI by exploiting spatial and temporal sparsity. Magn. Reson. Imag. (2016).

4. Ulas, C. et al. Spatio-temporal MRI reconstruction by enforcing local and global regularity via dynamic total variation and nuclear norm minimization. IEEE International Sym. on Biomed. Imag. (ISBI) (2016).

5. Raguet, H. et al. A generalized forward-backward splitting. SIAM J. on Imag. Sci. (2013).

6. Lebel, R.M. et al. Highly accelerated dynamic contrast enhanced imaging. Magn. Reson. Med. (2014).

7. Trémoulhéac, B. et al. Dynamic MR image reconstruction-separation from undersampled (k-t)-space via low-rank plus sparse prior. IEEE Trans. Med. Imag. (2014).

8. Vasanawala, S.S. et al. Practical Parallel Imaging Compressed Sensing MRI: Summary of two years of experience in accelerating body MRI of Pediatric patients. IEEE International Sym. on Biomed. Imag. (ISBI) (2011).

Figures

Figure 1. Spatial reconstructions of a single frame and time-intensity curves (TIC) averaged over the region of interests (ROIs) of Subject 1 (A) and Subject 2 (B) obtained with an 8-fold acceleration factor. Subfigure (A) also displays an exemplary undersampling mask in the bottom-left figure. For each frame, close-up views of two regions (yellow and green square) are also displayed. Subfigure (B) shows the TICs obtained from both non-tumor (nt) and tumor (tmr) region. Our method achieves the most accurate estimation of peaks and temporal patterns of perfusion signal, whereas spatial reconstructions are quite close to those obtained by SparseSENSE.

Figure 2. Perfusion parameter maps (CBF, CBV, MTT) of Subject 3 obtained by different methods with an 8-fold acceleration. The tumor region is marked by a white arrow in the Ground Truth CBF image. The proposed method results in perfusion maps where most of the structures are preserved and appear sharper compared to SparseSENSE, but some finer details are missing due to undersampling. The kt-RPCA reconstruction method produces highly inaccurate perfusion maps as expected by the mismatch of TICs shown in Figure 1. This method does not explicitly exploit variation in temporal domain, which makes it inadequate for quantitative PWI.

Figure 3. Perfusion parameter maps (CBF, CBV, MTT) of Subject 1 resulting from our proposed reconstruction method with respect to different acceleration factors and Ground Truth (GT) perfusion maps for comparison. The estimated perfusion maps appear highly accurate up to 8-fold acceleration but the maps start to deteriorate and show over-smooth regions at higher acceleration rates.

Figure 4. Bland-Altman plots and 95% confidence intervals within two red lines for CBF (top) and CBV (bottom) parameters of Subject 4 depending on different acceleration factors, resulting from our proposed reconstruction. The bias and variance of the difference between estimated and ground truth parameter values generally become larger when the acceleration rate increases. The estimated concordance correlation coefficients (CCCs) are displayed at the top-left corner of each plot. CCCs decrease with increasing acceleration, which coincides with the changes of bias and variance.

Table 1. Average concordance correlation coefficients (CCCs) of two perfusion parameters (CBF, CBV) obtained from five subject’s data with respect to increased acceleration rates. The values in brackets refer to CBF and CBV, respectively. The best values for each acceleration rate are highlighted in bold. Our method yields the best CCCs up to 8-fold acceleration and result in very similar quantitative values like SparseSENSE at 12-fold and 16-fold accelerations. The kt-RPCA method performs even worse than Zero-filled reconstruction since it leads to over-smoothing of the temporal perfusion signal, which can be easily observed in Figure 1.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0209