Purpose

Chemical exchange saturation transfer (CEST) is a new contrast mechanism in MRI, and several promising applications have been investigated such as brain tumors, stroke, and pH measurements [1]. However, a successful application of CEST is hampered by its time-consuming acquisition. SENSE [2] is a widely used parallel imaging method to accelerating MRI, which utilizes the sensitivity of the phased-array coils to provide spatial information for image reconstruction. However, SENSE is limited in CEST by reconstruction accuracy [3]. Compressed sensing (CS) [4,5] provides another way to accelerate MRI reconstruction, which utilizes the sparse prior information embedded in the MRI data. Blind compressed sensing (BCS) is a new CS method for dynamic MRI, which uses data correlation in spatial-temporal domain [6], and was recently applied for CEST imaging [7,8]. However, the original BCS method does not include coil sensitivity in the reconstruction. We propose a parallel-BCS (PBCS) method combining spatial-temporal dictionary and coil sensitivity to further accelerate CEST acquisition. The proposed method improves the accuracy of brain reconstruction even at high acceleration factor R=8.

Methods

CEST data has high spatial-temporal correlation, so only few temporal basis functions are enough to describe the temporal behavior [7,8]. Based on this assumption, BCS models the individual, frequency-offset, CEST images as a product of the sparse coefficient matrix and temporal basis. While the traditional BCS method only addresses sparsity in the coefficient matrix, we combine the sensitivity and the spatial-temporal dictionary to better utilize the prior information in CEST imaging. The algorithm is expressed as: $$$\min_{U,V} \sum_l \parallel F(S_lUV)-d_l \parallel _2^2 + \alpha \parallel U \parallel _1 + \beta \parallel V \parallel _2^2$$$, where $$$ U $$$ is the coefficient matrix, $$$V$$$is temporal basis, $$$ F $$$ is the undersampling Fourier operator, $$$S_l$$$ and $$$d_l$$$ are the sensitivity and undersampled k-space data from the l-th coil, $$$\parallel \cdot \parallel _1$$$ is the l1-norm to constraint on the sparsity of the coefficient matrix, $$$\parallel \cdot \parallel _2^2$$$ is the energy regularization term on temporal basis, $$$\alpha$$$ and $$$\beta$$$ are regularization parameters. The coil sensitivities were estimated with ESPIRiT [9] from the auto-calibration-signal (ACS) data. Measurements were performed on a Philips 3T Ingenia scanner using a 32-channel head coil. The phantom consists of five tubes of iopamidol solution with pH values of 6.0, 6.5, 7.0, 7.5, and 8.0. The tubes were immersed in a water-filled container. In vivo human brain data (n=3) was also collected. All CEST images were acquired with a TSE sequence, TR/TE=4200/6.4ms, slice thickness=4.4mm, matrix=240x240, FOV=240x240mm. The saturation RF consisted of a train of 40 Hyper-Secant pulses each of 49.5ms duration with 0.5ms intervals; 31 offset points were swept between ±1000Hz in steps of 67Hz with one additional image acquired without saturation, for normalization. The saturation power in the phantom was 1.6μT. In vivo, three levels were tested: 0.7μT, 1.2μT, and 1.6μT. CEST processing used WASSR [10] for B₀ inhomogeneity correction. The MTR_asym­ maps were calculated at 4.2ppm for phantom, and 3.5ppm (APT, amide proton transfer) for brain. We evaluated the performance of BCS and PBCS by performing retrospective Cartesian undersampling. Cartesian trajectory schemes used variable density undersampling pattern [5]. In the phantom, acceleration factor R=5 was used, for brain the acceleration factors were R=4 and 8.

Results and Discussion

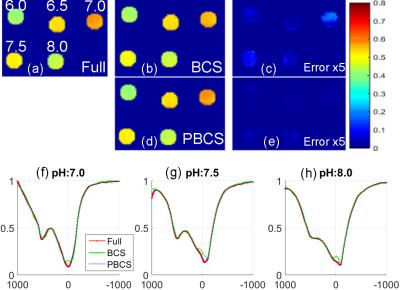
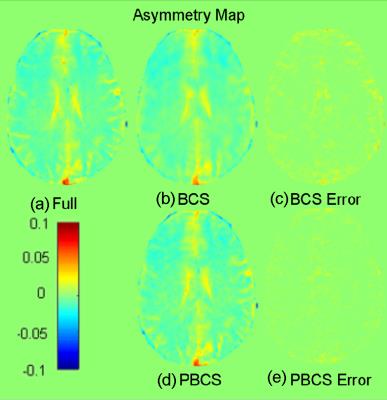
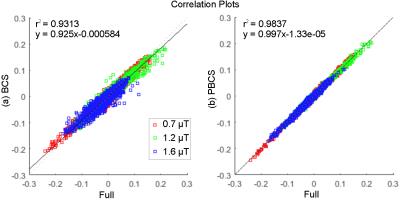
Fig. 1 compares MTR_asym asymmetry maps and Z-spectra reconstructed with fully sampled, BCS, and PBCS for different pH values. The reconstruction error in Fig.1 demonstrates that PBCS performs better than BCS. The BCS Z-spectrum is fairly accurate in most of the range but underperforms PBCS at the range near the zero-frequency offset. Fig. 2 and Fig. 3 compare MTR_asym and correlation plots reconstructed with fully sampled, BCS, and PBCS for the in vivo brain data. In the asymmetry maps, both methods result in good reconstructions, but BCS leads to larger errors. Fig.4 demonstrates correlation plots for different power values obtained using R=4 in another set of brain data. From the correlation plots and r² values it is evident that PBCS leads to higher correlation with the fully sampled images, as compared to the BCS method. Similar to other methods, PBCS performs better when subject motion is reduced and where higher acceleration factors can be obtained in highly cooperative subjects.

Conclusion

We propose a coil-sensitivity weighted parallel spatial-temporal sparse dictionary learning algorithm, which is an extension to the BCS method. Phantom and in vivo results demonstrate that the proposed method is able to improve BCS for CEST imaging. Work is in progress to evaluate the method in larger populations of healthy and patient volunteers, and to analyze different undersampling schemes.

Acknowledgements

The authors thank Dr. Sajan Goud Lingala and Dr. Michael Lustig for making BCS code and ESPIRiT code available online. The authors thank Dr. Asghar Hajibeigi (University of Texas Southwestern Medical Center) for phantom preparation. This work is supported in part by the NIH grant R21 EB020245 and by the UTSW Radiology Research fund.