Synopsis

Eddy currents distort images and confound diffusion tensor reconstruction. In this work, convex optimized diffusion encoding (CODE) was extended to include an eddy current nulling term (EN-CODE) to achieve minimum TE diffusion tensor imaging (DTI) without eddy current distortions. EN-CODE was evaluated in simulations and through imaging in phantoms and healthy subjects. EN-CODE achieves distortion reduction on par with the existing twice refocused spin echo (TRSE) technique with a substantially shorter TE.

Introduction

The large gradients used in diffusion tensor MRI (DTI) often lead to direction-dependent image distortions from eddy currents that corrupt tensor reconstruction. The twice refocused spin echo (TRSE) diffusion encoding scheme [1] largely eliminates this issue by nulling eddy currents with carefully timed bipolar gradients at the cost of substantially longer echo times (TE) compared to standard monopolar encoding (MONO).

Convex optimized diffusion encoding (CODE) [2] generates time-optimal diffusion encoding waveforms for a given b-value subject to gradient hardware constraints and pulse sequence timing. The objective was to achieve eddy current nulled diffusion encoding with minimum TE by adding an eddy current nulling constraint to the CODE framework (EN-CODE).

Methods

The eddy current field (ε) from an arbitrary encoding gradient, G(t) can be modeled by: ε(t,λ) $$$ \propto $$$ dG(t)/dt * e^-t/λ where λ is the time constant of eddy current decay and * is the convolution operator [3].

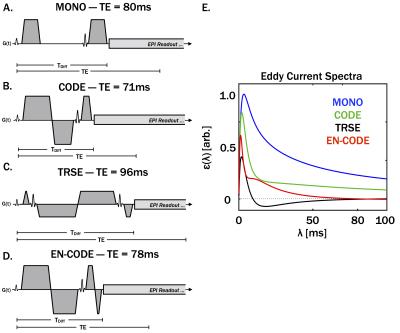
EN-CODE gradients were designed for b=1000s/mm² using the CODE framework with the added constraint: ε(T_Diff,λ_NULL)=0. T_Diff is the end of the diffusion encoding gradients. We targeted λ_NULL=80ms, which is an optimal value empirically determined for our system, as in Reese et al. [1]. Analogous waveforms were generated using TRSE (λ_NULL=80ms) as well as MONO and CODE (without eddy current nulling). Eddy current spectra were then simulated for each waveform using the above equation for ε at t=T_Diff for a range of λ (0-100ms, Δλ=1ms) and normalized by the overall maximum.

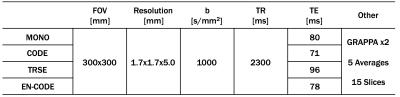
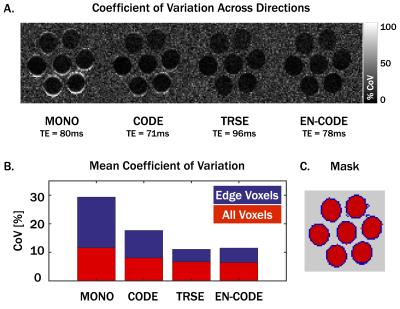
MONO, CODE, TRSE and EN-CODE protocols are tabulated in Figure 1. A phantom containing cylindrical vials of water submerged in a fluid with negligible MRI signal (Fomblin) was scanned at 3T (Prisma, Siemens, GMAX=76mT/m) with three diffusion encoding directions (x, y and z). For each sequence, the voxel-wise coefficient of variation (CoV) was calculated across the three encoding directions to measure image distortions. The mean CoV was calculated within all water voxels as well as in edge voxels at water-Fomblin interfaces.

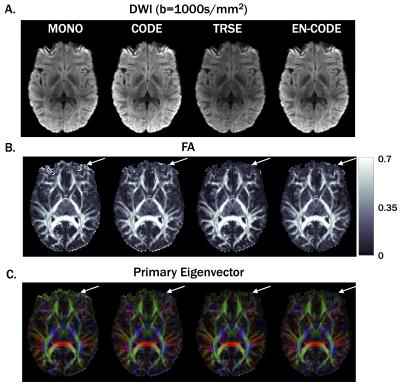
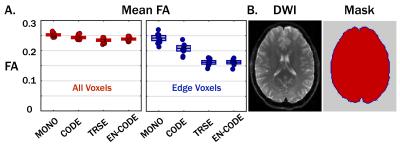
Neuro DTI was acquired in healthy volunteers (N=10) for further comparison between techniques using 20 diffusion encoding directions (Fig. 1). FA maps were generated from the reconstructed tensors. Mean global FA was measured for each technique within a whole brain mask and a mask containing only brain edges.

Results

The diffusion encoding gradient waveforms and their simulated eddy current spectra are shown in Figure 2. EN-CODE exactly nulls eddy currents at λ=80ms and substantially reduces them for all λ compared to MONE and CODE. TRSE increased TE by 18ms compared with EN-CODE, but achieved similar eddy current spectral improvements.

Eddy current distortions in phantoms for MONO and, to a lesser extent, CODE induced higher CoV near phantom edges compared to TRSE and EN-CODE, which both eliminated these distortions and led to mean CoV <40% of MONO in edge voxels (Figure 3).

A representative in vivo example is shown in Figure 4. Eddy current distortions were evident in MONO and CODE (artificially high FA anteriorly). These distortions were not present in TRSE or EN-CODE. Global FA analysis (Figure 5) shows that MONO had the highest mean edge voxel FA (0.24±0.02), which decreased with CODE (0.21±0.02, p=3x10^-4) and more so with TRSE (0.16±0.01, p=3x10^-10) and EN-CODE (0.16±0.01, p=3x10^-10). Due to its shorter TE, EN-CODE had higher apparent SNR than TRSE.

Discussion

Simulations, phantom experiments, and in vivo imaging all indicate that EN-CODE largely eliminates eddy current distortions in DTI with a substantially shorter TE than TRSE and a slightly shorter TE than MONO.

While all sequences used b=1000 s/mm² and the minimum possible TE, gradient amplitudes were lower with TRSE (46mT/m) than all others (76mT/m) which led to lower slew rates (ramp times were fixed). It is notable that EN-CODE achieved equivalent eddy current suppression with both higher gradient amplitudes and slew rates. Note that in the TRSE sequence design larger gradient amplitudes do not permit significantly reducing TE.

Finsterbusch’s tripolar eddy current nulling scheme [4] also reduced TE compared with TRSE in many scenarios (e.g. long EPI readouts). EN-CODE has similar benefits, but has the added flexibility of optimally conforming to any sequence parameters.

Conclusion

Acknowledgements

References

1. Reese TG, Heid O, Weisskoff RM, Wedeen VJ. Reduction of eddy-current-induced distortion in diffusion MRI using a twice-refocused spin echo. Magn Reson Med. 2003;49(1):177-82.

2. Aliotta E, Wu HH, Ennis D. Convex Optimized Diffusion Encoding (CODE) Gradient Waveforms for Minimum Echo Time and Bulk Motion Compensated Diffusion Weighted MRI. Magnetic Resonance in Medicine. 2016.

3. Liang Z-P, Lauterbur PC. Principles of Magnetic Resonance Imaging: A Signal Processing Perspective: Wiley-IEEE Press; 1999.

4. Finsterbusch J. Eddy-current compensated diffusion weighting with a single refocusing RF pulse. Magn Reson Med. 2009;61(3):748-54.