0177

Accelerated k-q diffusion MRI reconstruction using Gaussian processes

Wenchuan Wu¹, Peter J Koopmans², Jesper Andersson², and Karla L Miller²

¹FMRIB, University of Oxford, Oxford, United Kingdom, ²FMRIB, University of Oxford

Synopsis

Diffusion MRI commonly acquires multiple diffusion volumes (directions), which shares plentiful common features. In this work, we propose integrating Gaussian Processes into image reconstruction to utilize the shared information between diffusion volumes to reduce image artefacts associated with parallel imaging.

Purpose

To demonstrate the use of Gaussian processes to improve reconstruction of accelerated diffusion MRI data by leveraging shared local information in q-space.

Introduction

Diffusion MRI typically acquires a large number of diffusion volumes (directions). These volumes contain an abundance of common features (e.g. structural boundaries, mean signal attenuation), yet each volume is usually reconstructed independently. The shared information between the spatial and diffusion-weighting (q-space) domains has been successfully exploited in image analysis, where Gaussian processes have been used to remove image distortion from eddy currents, and to predict “missing” q-space samples¹. We propose to integrate Gaussian processes into image reconstruction directly to leverage shared information between the k and q domains to reduce image artifacts associated with parallel imaging.

Methods

Diffusion signal, considered as a stochastic function in q-space domain, can be modelled as a Gaussian process, whose distribution is governed by a mean function and a covariance function². Unlike parametric modelling of diffusion signal, Gaussian processes don’t make explicit assumption of underlying tissue structures. Instead, it measures the similarities between q-space samples and use it to predict unseen data from training data. Here, we propose to reconstruct diffusion MRI signals with a Gaussian processes model. The reconstruction is formulated as:

$$u=\arg \min_u\sum_i\sum_j\parallel MFs_ju_i-d_{i,j}\parallel_2^2+\lambda\parallel P^*u-WP^*u \parallel_2^2 [1]$$

where d_i,j: k-space data of the i^th diffusion volume acquired from the j^th coil; u=[u₁,u₂,...,u_{n_d}]: unknown image; M: k-space sampling operator; F: Fourier encoding operator; s=[s₁,s₂,...,s_{n_c}]: coil sensitivity; W: linear prediction matrix learned from the Gaussian processes³. λ: regularization parameter controlling the strength of constraint by Gaussian processes; P: motion-induced phase errors during diffusion encoding, which can be obtained via a navigator⁴ or estimated from the data itself (self-navigation⁵).

The hyper-parameters required by Gaussian processes were estimated from the reconstructed images and updated during the iteration. The reconstruction pipeline consists of three steps:1. Initial reconstruction of each diffusion-weighted volume independently using conventional parallel imaging; 2. Estimation of Gaussian Processes hyper-parameters using reconstructed images from previous iteration; 3. Reconstruction of all diffusion volumes using Eq.[1]. The reconstruction iterates between steps 2 and 3 until convergence.

A optimized locally-incoherent k-q sampling scheme is used (see another abstract from our group), in which in-plane under-sampling of k-space varies across q-space locations. This incoherent distribution of samples in the joint k-q domain means that common spatial features that might be lost by independent volume reconstruction can be potentially recovered from other q-space locations.

A diffusion MRI data set with 128 directions and b=1000 s/mm² is simulated using a ball-and-stick model^6,7. Simulations include coil sensitivity maps measured from an 8-channel coil and high in-plane acceleration factor R=4,6,10 (with R=10 exceeding the theoretical parallel imaging limits).

Data were acquired from two subjects using EPI with R=3 and 6 (Siemens 7T with 32ch receiver, bipolar encoding, FLEET sensitivity mapping⁸, navigator spin-echo). Five sets of b=0 data were acquired using multi-shot EPI (6 shots). A conventional diffusion MRI dataset (R=3, PF=6/8) was also acquired at the same resolution. Other parameters given in figure captions.

Simulated and in vivo data are reconstructed using conjugate-gradient-SENSE⁹ and our Gaussian process method, then analysed using both tensor and multi-fibre models^6,⁷.

Results

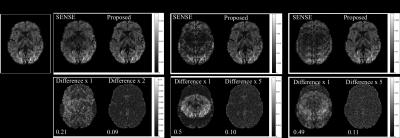
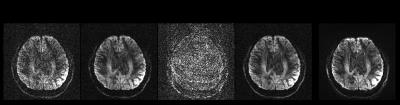
Fig.1 shows simulation results for three in-plane reduction factors. Conventional parallel imaging using the simulated 8-channel coil results in clear g-factor artifacts in the middle of the brain for R=4; the reconstruction breaks down completely for R=6 and 10 due to the limited number of channels. The Gaussian process reconstruction drastically reduces noise and artefacts, resolving aliasing even with R=10 (exceeding the number of channels).

For in-vivo data (Fig.2), conventional reconstruction at R=6 suffers from low SNR. The Gaussian processes significantly improve reconstruction both with and without navigator correction. Difference images illustrate the effective removal of noise and aliasing artefacts using Gaussian processes.

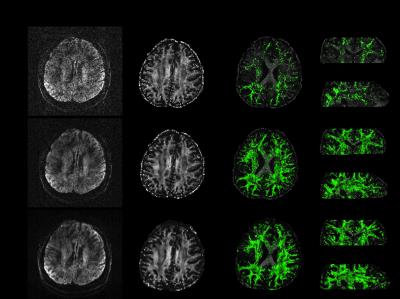
Propagation of noise and residual artefacts in diffusion quantification are demonstrated in Fig.3. At R=6, conventional parallel imaging fails to capture many secondary fibre populations, likely due to low SNR. This information is well preserved in the Gaussian processes reconstruction, indicating the angular information needed to estimate several fibres is not being blurred out by the Gaussian processes.

Discussion and Conclusion

We demonstrated a reconstruction method utilizing the sharable information among diffusion volumes, which improves SNR and reduces residual aliasing for under-sampled diffusion MRI data. This initial demonstration focused on in-plane acceleration, but the method should be compatible with through-plane acceleration (simultaneous multi-slice/3D acquisition), as well as multi-dimensional acceleration. Current implementation has not considered gross subject motion, and incorporation of motion correction would improve the reconstruction further, which will be investigated in the future work.

Acknowledgements

Funding for this work was provided by the Marie Curie Initial Training Network program (FP7-PEOPLE-2012-ITN-316716, WW) and Wellcome Trust fellowships (091509/Z/10/Z, KM and WT100092MA,PK).

References

1. Jesper L. R. Andersson, Mark S. Graham, Eniko Zsoldos and Stamatios N. Sotiropoulos. Incorporating outlier detection and replacement into a non-parametric framework for movement and distortion correction of diffusion MR images. NeuroImage DOI: 10.1016/j.neuroimage.2016.06.058.

2. Jesper L.R. Andersson and Stamatios N. Sotiropoulos. Non-parametric representation and prediction of single- and multi-shell diffusion-weighted MRI data using Gaussian processes. NeuroImage, 122:166-176, 2015.

3. Rasmussen, C.E.,Williams, C.K.I., 2006. Gaussian Processes for Machine Learning. The MIT Press, Cambridge, Massachusetts.

4. Butts K, deCrespigny A, Pauly JM, Moseley M. Diffusion-weighted interleaved echo-planar imaging with a pair of orthogonal navigator echoes. Magnetic Resonance in Medicine 1996;35(5):763-770.

5. Chen Nk, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). NeuroImage 2013;72:41-47.

6. T.E.J. Behrens, M.W. Woolrich, M. Jenkinson, H. Johansen-Berg, R.G. Nunes, S. Clare, P.M. Matthews, J.M. Brady, and S.M. Smith. Characterization and propagation of uncertainty in diffusion-weighted MR imaging. Magn Reson Med, 50(5):1077-1088, 2003.

7. T.E.J. Behrens, H. Johansen-Berg, S. Jbabdi, M.F.S. Rushworth, and M.W. Woolrich. Probabilistic diffusion tractography with multiple fibre orientations. What can we gain? NeuroImage, 23:144-155, 2007.

8. Polimeni JR, Bhat H, Witzel T, Benner T, Feiweier T, Inati SJ, Renvall V, Heberlein K, Wald LL. Reducing sensitivity losses due to respiration and motion in accelerated echo planar imaging by reordering the autocalibration data acquisition. Magnetic resonance in medicine. 2016;75(2):665-79.

9. Pruessmann KP, Weiger M, Börnert P, Boesiger P. Advances in sensitivity encoding with arbitrary k-space trajectories. Magnetic Resonance in Medicine 2001;46(4):638-51.

Figures

Fig. 1. Reconstruction on simulated data using SENSE and the proposed method. The first row shows the ground truth image and reconstructions at different reduction factors. The second row shows the difference images between the reconstructions and the ground truth with RMSE shown on the bottom left. (Difference images are scaled for better visualization).

Fig. 2. In vivo data acquired from Subject 1. Conventional SENSE suffers from substantially amplified noise even with a large number of coil elements (32 here). The proposed method improves the reconstruction with significantly reduced noise and artefacts. Reconstructions with and without navigator demonstrate very similar performance, indicating it’s possible to get rid of the navigator acquisition, which can reduce the scan time and SAR burden (~20%, from the refocusing pulse for the navigator). Scan parameters: resolution 1.3x1.3x2 mm³, b=1000s/mm², 128 directions. TR/TE=3.5s/90ms, 20 slices. R=3 and 6. R=3 data was acquired with partial Fourier of 6/8.

Fig. 3. In vivo data acquired from Subject 2. The noise and residual artefacts in SENSE reconstruction propagate into diffusion quantification, particularly affecting the estimation of multi-fibre populations within a single voxel. The SENSE reconstruction of R=3 data is used as reference here. In the SENSE results of R=6 data, many second fibre populations are lost, likely due to the low SNR of the raw data. Whereas the proposed method robustly recovered the second fibres. Scan parameters: Resolution 1.5mm isotropic, b=1000s/mm²,128 directions, TR/TE=6.5s/82ms, 40 slices, R = 3 and 6. R=3 data was acquired with partial Fourier of 6/8.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0177