Synopsis

Reconstruction of highly under-sampled FMRI data using low-rank constraints can suffer from loss of fidelity at high acceleration factors, or when signals are relatively weak. We introduce a method for improving reconstruction fidelity using external constraints, i.e., informative signals that are not data-derived. We show that this improves FMRI reconstruction quality in a number of conditions, including detecting subtle latency shifts between brain regions, and improving resting state network characterization using simultaneously acquired EEG information. We further show that this approach works with noisy or approximate constraints, and the derived benefit is commensurate with the information content they provide.

Introduction

We propose a method for improving accelerated FMRI data reconstruction using external measures such as experimental design considerations or simultaneously acquired EEG. This approach extends rank-constrained FMRI¹, which has enabled robust under-sampled recovery of high-variance information based on network modelling. However, rank-constrained approaches rely upon the strength of the functional components, and when under-sampling factors are high or the components are subtle, functional data recovery can be poor or incomplete².

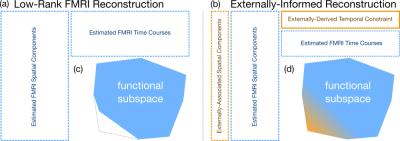
We incorporate external information into the rank-constrained reconstruction framework by enforcing its presence in the low-rank temporal subspace, facilitating the recovery of information that would be otherwise irretrievable at the chosen acceleration factors. We also show that the external measure(s) need not be completely accurate, so long as there is some degree of shared variance with the data. This is demonstrated in simulated and experimental data, where to our knowledge, this work constitutes the first demonstration of using information from simultaneously acquired EEG to inform and improve the reconstruction of FMRI data.

Methods

Our rank constrained FMRI reconstruction framework solves:

$$min || y-\Phi(UV^{*})|| s.t. rank(UV^{*})=r$$

where $$$U$$$ and $$$V$$$ correspond to the spatial and temporal components of the space-time data, and $$$\Phi$$$ incorporates k-space trajectory and coil sensitivity information.

Given an external temporal constraint $$$v$$$, which can be an $$$n\times 1$$$ vector or an $$$n\times c$$$ matrix with $$$c$$$ different constraints, we solve:

$$min ||y-\Phi(UV^{*})|| s.t. rank(UV^{*})=r, v\in V$$

This constraint enforces the explicit inclusion of $$$v$$$ in the subspace spanned by $$$V$$$, where remaining high-variance temporal components are estimated from the under-sampled data as usual (Fig. 1). We implemented this by iteratively removing the projection of the estimate onto $$$v$$$, estimating the $$$r-c$$$ remaining components, and enforcing data consistency on the sum until convergence.

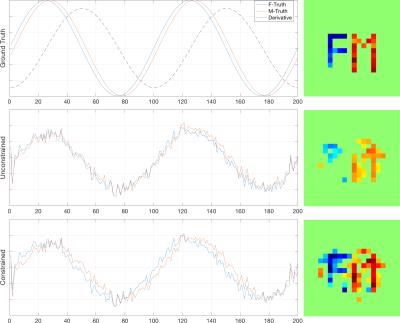
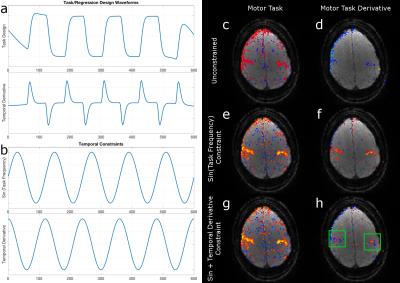
We tested this approach in simulations using temporal constraints correlatedwith a ground truth component (by r2=0.2, 0.5) at acceleration factors of R=4/8/16, compared to a low-rank reconstruction using no external constraint. We also simulated reconstruction of two ROIs with identical time-courses that have a small latency offset, at R=10. Data were also acquired using radial Cartesian sampling³ at 3T, reconstructed at TR = 500 ms (2 mm isotropic, R=10), in 30 s/30 s off/on block design finger tapping experiments with a self-cued 1 s delay between the right and left hands. In both cases, temporal derivatives were used as temporal constraints to capture the latency differences.

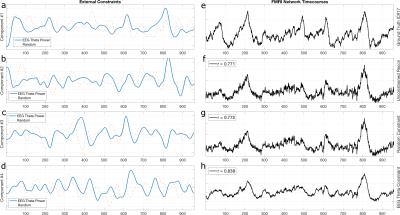
Finally, 4-slice fully-sampled EPI (3T, TR_vol=200 ms) data with simultaneously acquired EEG (32-channels, Brain Products) were used to evaluate the benefit of EEG information in a retrospectively under-sampled reconstruction. The four highest variance theta band power time-courses (across channels) were extracted from the artefact-corrected EEG data. These were convolved with a canonical HRF, and used as temporal constraints in the under-sampled reconstruction of the EPI data (R=10), assuming that EEG signals correlate with FMRI resting state time-courses⁴.

Results

In Fig. 2, the temporal constraints are shown, alongside the recovered z-stat maps (|z|>3) from a regression analysis. The ROI was well characterized at low acceleration factors, but with increasing acceleration, only the constrained reconstructions showed good recovery, despite only using constraints that only partially correlated with the ROI time-course.

Fig. 3 shows the latency simulation results, where both the recovered time-courses and the z-stat maps (|z|>3) show improved separation of the time-shifted components when the temporal derivative is included in reconstruction. In the experimental data using sinusoidal constraints (Fig. 4), positive/negative relative latencies in left and right motor cortices were only identified when the temporal derivative constraint was used (Fig. 4h, green boxes).

Fig. 5a-d shows the externally derived EEG theta power time-courses, and Fig. 5e shows a single ICA time-course derived from the FMRI ground truth, alongside the representation of this network time-course in the reconstructed temporal components (Figs. 5f-h). The EEG-informed reconstruction improves the characterisation of the ICA component (r=0.84 vs r=0.77), while randomly generated time-courses convolved with the same HRF convey no positive or negative impact (r=0.77).

Discussion

Acknowledgements

References

1. Chiew, M., Smith, S. M., Koopmans, P. J., Graedel, N. N., Blumensath, T., & Miller, K. L. (2015). k-t FASTER: Acceleration of functional MRI data acquisition using low rank constraints. Magnetic Resonance in Medicine, 74(2), 353–364.

2. Chiew, M., Graedel, N. N., Mcnab, J. A., Smith, S. M., & Miller, K. L. (2016). Accelerating functional MRI using fixed-rank approximations and radial-cartesian sampling. Magnetic Resonance in Medicine (Online Early View)

3. Graedel, N. N., Mcnab, J. A., Chiew, M., & Miller, K. L. (2016). Motion correction for functional MRI with three-dimensional hybrid radial-Cartesian EPI. Magnetic Resonance in Medicine (Online Early View)

4. Mantini, D., Perrucci, M. G., Del Gratta, C., Romani, G. L., & Corbetta, M. (2007). Electrophysiological signatures of resting state networks in the human brain. Proceedings of the National Academy of Sciences of the United States of America, 104(32), 13170–13175.

5. Lam, F., Zhao, B., Liu, Y., Liang, Z.-P., Weiner, M., & Schuff, N. (2013). Accelerated fMRI using Low-Rank Model and Sparsity Constraints. Proceedings of the 21st ISMRM, #2620.

6. Nguyen, H., & Glover, G. H. (2014). Field-corrected imaging for sparsely-sampled fMRI by exploiting low-rank spatiotemporal structure. Proceedings of the 22nd ISMRM, #327.