0140
Accelerated Cardiac Diffusion Tensor Imaging Using a Joint Low-Rank and Sparsity Constraint1Biomedical Imaging Research Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, 2Department of Bioengineering, University of California, Los Angeles, Los Angeles, CA, United States, 3Heart Institute, Cedars-Sinai Medical Center, Los Angeles, CA, United States, 4Department of Pathology, Cedars-Sinai Medical Center, Los Angeles, CA, United States
Synopsis
We present an image reconstruction technique to accelerate cardiac diffusion tensor imaging by jointly applying a low-rank and spatial sparsity constraint. We evaluated four acquisition schemes at different undersampling levels on 9 ex vivo diseased human heart, evaluating the reconstruction quality based on the resulting helix angle (HA) maps and helix angle transmurality (HAT) values. A Wilcoxon signed rank test was performed to statistically evaluate changes in HAT to determine the highest achievable acceleration factor for each acquisition scheme. Our framework shows promise in greatly reducing scan time while preserving the fiber architecture features of heart failure.
Introduction
Cardiac Diffusion Tensor Imaging (CDTI) is a powerful noninvasive tool capable of revealing the fiber orientation and structure of the myocardium1-2. However, CDTI is limited by its long scan time (>20 minutes). Potential approaches to address this problem are low-rank modeling which has successfully been used to accelerate brain diffusion MRI3 and spatial-temporal imaging4-6, and sparse modeling (compressed sensing) which has successfully been used to free-breathing MRI7 and 3D angiography8. In this work we apply a low-rank model alongside spatial transform sparsity constraints to accelerate CDTI, reducing scan time while preserving the image features used to assess heart failure. We compare four acquisition schemes at varying undersampling levels and evaluate the resulting helix angle (HA) maps, and global helix angle transmurality (HAT) values against the HA maps and HAT values from fully sampled data.Methods
The low-rank structure in cardiac diffusion-weighted images lies in the strongly correlated behaviors of diffusion-weighted signals at different voxels3. This correlation induces low-rankness of the matrix $$$\mathbf{S}=[s_1,s_1,\dots,s_N]$$$, where the diffusion-weighted image for direction $$$n$$$ is reshaped as a vector $$$s_n\in\mathbb{C}^{M}$$$, such that it can be factorized as $$$\mathbf{S}=\mathbf{U}_\mathrm{s}\mathbf{V}_\mathrm{d}$$$, where $$$\mathbf{V}_\mathrm{d}\in\mathbb{C}^{L\times{N}}$$$ contains “diffusion basis functions” that span the diffusion subspace, and $$$\mathbf{U}_\mathrm{s}\in\mathbb{C}^{M\times{L}}$$$ contains spatial coefficients. $$$\mathbf{S}$$$ is a low-rank matrix when $$$L\lt\min\{M,N\}$$$. Here we enforce the low-rank property by predefining $$$\mathbf{V}_\mathrm{d}$$$ from center k-space data via singular value decomposition3; we further include a sparsity constraint to also leverage the compressed sensing framework6. Our reconstruction model is thus:$$\mathbf{S}=\hat{\mathbf{U}}_\mathrm{s}\mathbf{V}_\mathrm{d}\textrm{, where }\hat{\mathbf{U}}_\mathrm{s}=\arg\min_{\mathbf{U}_\mathrm{s}}\|\mathbf{d}-\Omega(\mathbf{F}_\mathrm{s}\mathbf{U}_\mathrm{s}\mathbf{V}_\mathrm{d})\|_2^2+\lambda\|\mathbf{W}\mathbf{U}_\mathrm{s}\mathbf{V}_\mathrm{d}\|_1\qquad(1)$$where $$$\Omega$$$ is the k-space sampling operator, $$$\mathbf{F}_\mathrm{s}$$$ applies the spatial Fourier transform, $$$\mathbf{W}$$$ applies a spatial sparsifying transform, and $$$\lambda$$$ is the regularization parameter. Equation (1) can be efficiently solved by an ADMM algorithm.
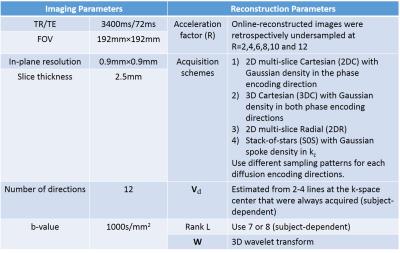
Our study was performed on 9 ex vivo hearts extracted from heart failure patients (Cedars-Sinai Medical Center Heartome database). Data was acquired on a 3T mMR PET/MRI Siemens scanner using a diffusion-weighted spin echo sequence. Table 1 shows the acquisition and reconstruction parameters. HAT was calculated by radially sampling the HA along 25 transmural directions and fitting the slope between HA and transmural depth using linear regression. A Wilcoxon signed rank test was performed to evaluate the difference between fully sampled-derived HAT (reference) and undersampled-derived HATs at varying acceleration factors.
Results
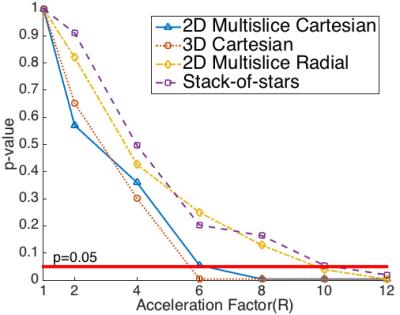
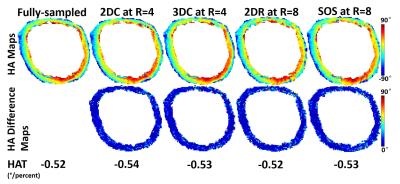
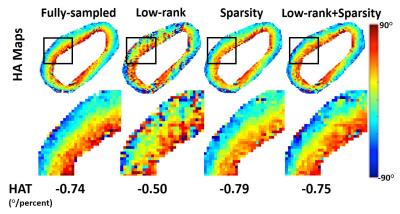
Figure 2 shows the p-value plotted against R for all four acquisition schemes with joint low-rank and sparsity constraints, where R is the acceleration factor compared to the Cartesian Nyquist rate. For 2D multi-slice Cartesian (2DC) and 3D Cartesian (3DC), the p-value remains insignificant (p$$$\gt$$$0.05) for R$$$\leq$$$4. For 2D multi-slice Radial (2DR) and Stack-of-stars (SOS), the p-value remains insignificant all the way up to R=8. Figure 3 shows the HA maps of a fully sampled image and its undersampled counterparts at R=4 using 2DC and 3DC trajectories and at R=8 using 2DR and SOS trajectories, as well as the difference maps between the fully sampled and each undersampled HA map. The HA map and HAT values with each undersampled dataset are similar to those with the fully sampled data. Figure 4 compares the use of either a single low-rank or sparsity constraint to the joint constraints, depicting the HA map of a fully sampled image and its undersampled counterparts at R=4 using 2DC as well as an enlarged area of each HA map. The HAT value with the joint constraints is close to the reference while those with single constraint are substantially different. The HA map with the joint constraints preserves more details than those with single constraint.Discussion
The p-value decreases as R increases, indicating that undersampling artifacts cause mean global HAT values to significantly differ from the gold standard. The p-value analysis shows that the 2DR and SOS trajectories have more potential to accelerate CDTI (R=4 Cartesian vs. R=8 Radial) while maintaining global HAT values. Neither low-rank constraint nor the sparsity constraint is sufficient to preserve the HA map (and especially HAT) on its own, whereas the proposed joint constraint maintains the HA map and the global HAT.Conclusion
We proposed a reconstruction technique to accelerate cardiac diffusion tensor imaging (CDTI) by jointly applying a low-rank model and spatial sparsity constraint and compared four sampling schemes. We found an acceleration factor of 4 can be achieved for Cartesian sampling and a factor of 8 for radial sampling while preserving the global HAT measurements, which may enable us to detect the structural defects in the fiber architecture of heart failure patients’ explanted hearts. Our work has the potential to be applied to in vivo CDTI in the future with greatly reduced scan time.Acknowledgements
No acknowledgement found.References
1. Mekkaoui C, Reese T G, Jackowski M P, et al. Diffusion MRI in the heart. NMR in Biomedicine, 2015.
2. Nguyen C, Fan Z, Sharif B, et al. In vivo three-dimensional high resolution cardiac diffusion-weighted MRI: A motion compensated diffusion-prepared balanced steady-state free precession approach. Magnetic resonance in medicine, 2014, 72(5): 1257-1267.
3. Gao H, Li L, Zhang K, et al. PCLR: Phase-constrained low-rank model for compressive diffusion-weighted MRI. Magnetic resonance in medicine, 2014, 72(5): 1330-1341.
4. Liang Z P. Spatiotemporal imaging with partially separable functions. IEEE International Symposium on Biomedical Imaging, 2007: 988-991.
5. Pedersen H, Kozerke S, Ringgaard S, et al. k-t PCA: Temporally constrained k-t BLAST reconstruction using principal component analysis. Magnetic resonance in medicine, 2009, 62(3): 706-716.
6. Zhao B, Haldar J P, Christodoulou A G, et al. Image reconstruction from highly undersampled-space data with joint partial separability and sparsity constraints. IEEE transactions on medical imaging, 2012, 31(9): 1809-1820.
7. Feng L, Axel L, Chandarana H, et al. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magnetic resonance in medicine, 2016, 75(2): 775-788.
8. Lustig M, Donoho D, Pauly J M. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magnetic resonance in medicine, 2007, 58(6): 1182-1195.
Figures