Synopsis

MR Fingerprinting signal evolutions can be used to estimate partial volumes of tissues in addition to tissue relaxation times. Two approaches to tissue fraction estimation, a pseudoinverse calculation and dictionary-based or constrained solution, are quantitatively compared in the presence of four potential error sources. The constrained approach is found to more accurately estimate tissue fractions, and also to improve segmentation of pathology.

Background

It was recently demonstrated that MR Fingerprinting (MRF) can be used to estimate tissue fractions by modeling mixed voxel MRF signals as a weighted sum of known component signals, $$$D$$$ [1,2]:
$$S_{voxel} = D w$$
Partial volumes (PV) estimated by computing the pseudoinverse,
$$\hat{w} = (D^HD)^{-1}D^HS_{voxel}$$
must be normalized to obtain positive real tissue fractions (TF) which sum to unity. This normalization can result in errors from over-fitting of noise or other artifacts.

Recent work showed that a dictionary can be used to enforce a physical interpretation of tissue mixtures [3] and reduce the effect of over-fitting errors [4]. In this approach, a new dictionary of weighted sums of $$$D$$$ is constructed where $$$w$$$ is constrained to be real, positive, and summed to 1. Mixed voxel signals are matched to this PV dictionary based on the inner product to identify $$$w$$$.

In this work we quantitatively compared TF accuracy when estimated by the PV dictionary and pseudoinverse approaches in the presence of four error sources and assessed the ability to segment a metastatic brain tumor.

Materials & Methods

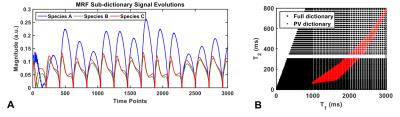
MRF dictionary entries with 3000 frames were simulated as described in [5]. Three entries were selected for $$$D$$$ (Fig1A). The PV dictionary of linear combinations of $$$D$$$ had 5151 entries with a reduced T₁ and T₂ range compared to the 5461 entries in the full MRF dictionary (Fig1B).

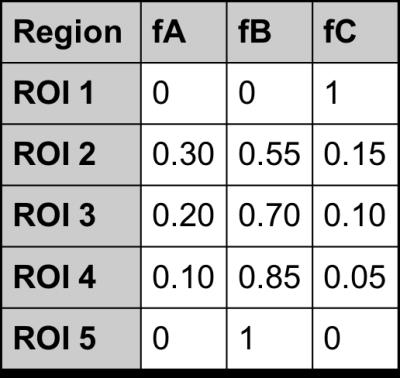
A digital phantom with two pure regions and three mixed regions with known proportions (Table 1) was populated such that each pixel contained the MRF signal of one tissue type from $$$D$$$. Each frame of the phantom was down-sampled to simulate voxel mixing. Four modifications were made to test accuracy in the presence of errors:

1. Noise: Gaussian white noise was added to k-space prior to down-sampling (8 noise levels tested, 25 repetitions each).

2. Undersampling: the down-sampled noise-free phantom was spiral undersampled (8 acceleration factors tested).

3. Tissue variation: the T₁ and T₂ for each tissue type was drawn from a distribution with fixed mean and varied standard deviation before populating the phantom. Mean T₁ and T₂ were fixed to match the values in $$$D$$$. Standard deviations were scaled to each mean (14 standard deviations tested, 25 repetitions each).

4. Model error: the standard deviation of each species T₁ and T₂ values were held constant at σ=0.05μ. Mean T₁ and T₂ of species A and C matched the values in D, while mean T1 and T2 of species B was varied between 90-110% of the values in $$$D$$$ (9 mean values tested, 25 repetitions each)

In each simulation, species fractions in the down-sampled phantom were computed both by pseudoinverse and by PV dictionary matching. Results were averaged over each region and plotted as mean and standard deviation across repetitions where applicable.

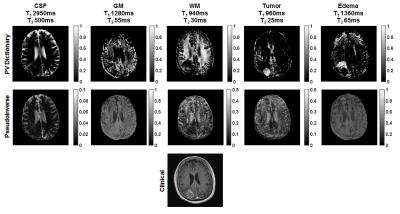
One patient with a colonergic metastatic brain tumor was scanned at 3T with MRF (Skyra, Siemens Healthcare, Erlangen Germany). Cerebrospinal fluid, grey matter, white matter, tumor, and edema fractions were estimated by both approaches using the same dictionaries. Normal tissue relaxation times were determined by 9-component k-means segmentation of MRF T₁ and T₂ maps of the contralateral hemisphere. Tumor relaxation times were determined from T₁ and T₂ in an ROI in the tumor core.

Results

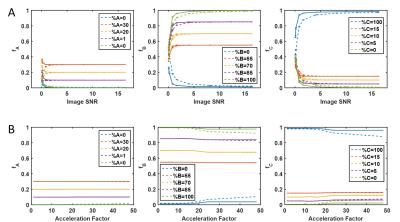
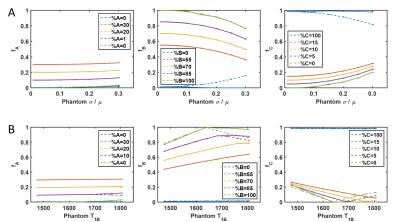
The PV dictionary approach to TF estimation is more robust to noise (Figure 2A) and undersampling artifacts (Figure 2B) than the pseudoinverse approach. When the average T₁ and T₂ of each tissue is accurately represented by $$$D$$$, TF estimated by both methods have similar accuracy and precision and are robust up to 10% variation in underlying T₁ and T₂ (Figure 3A); PV dictionary estimation is more robust to wider variation in tissue properties. When $$$D$$$ does not represent the mean tissue relaxation times, larger errors can occur (Figure 3B). Both methods fail when relaxation times in $$$D$$$ are overestimated; however TF error is limited by PV dictionary matching when relaxation times are underestimated.

In vivo, the pseudoinverse approach breaks down when additional tissue components are introduced. However, PV dictionary matching improves fraction accuracy, as demonstrated by clear segmentation of normal-appearing brain tissues, tumor tissue, and edema (Figure 4).

Discussion

Acknowledgements

References

[1] Ma et al. Magnetic Resonance Fingerprinting. Nature 2013; 495(7440):187-192.

[2] Deshmane et al. Validation of Tissue Characterization in Mixed Voxels Using MR Fingerprinting. Proc. ISMRM 2014; p.94.

[3] Deshmane et al. Enforcing a Physical Tissue Model for Partial Volume MR Fingerprinting. Proc. ISMRM 2016; p.2998.

[4] Cao et al. An Improved Tissue-Fraction MRF (TF-MRF) with Additional Fraction Regularization. Proc. ISMRM 2016; p.4223.

[5] Jiang et al. MR Fingerprinting using Fast Imaging with Steady State Precession (FISP) with Spiral Readout. Magnetic Resonance in Medicine 2015; 74(6):1621-1631.

[6] McGivney et al. Exploring Subvoxel Structures in Brain Tumors using Magnetic Resonance Fingerprinting. Submitted to ISMRM 2017.