0131

Intra-Voxel Spatial Resolution Using Magnetic Resonance Fingerprinting

Thomas Amthor¹, Karsten Sommer¹, Peter Koken¹, Jakob Meineke¹, and Mariya Doneva¹

¹Philips Research, Hamburg, Germany

Synopsis

We demonstrate the use of Magnetic Resonance Fingerprinting to retrospectively increase spatial resolution in slice-encoding direction, making use of the non-uniform nature of the excitation slice profile. Assigning individual fingerprints to substances present at different spatial positions within the excited voxel, a multi-compartment analysis recovers the spatial distribution of the components.

Purpose

Magnetic Resonance Fingerprinting (MRF) is a promising technique for tissue characterization and quantitative multi-parametric measurements [1, 2]. A train of RF pulses produces an MR signal unique for a certain tissue type, which can then be compared with a dictionary of known signals. By finding the best-matching linear superposition of dictionary entries, the composition of the voxel can be determined and a multi-compartment analysis is possible. In this work we extend the multi-compartment analysis to an intra-voxel spatial resolution in slice-encoding direction. This technique is based on the non-uniform nature of the excitation slice profile. Assigning individual fingerprints to substances present at different spatial positions within the excited voxel, a multi-compartment analysis will recover the spatial distribution of the components. This technique can be used to decrease MRF acquisition time, or to retrospectively increase the spatial resolution of a particular region of interest.

Methods

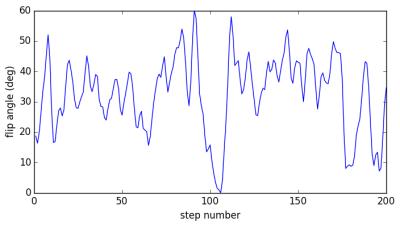
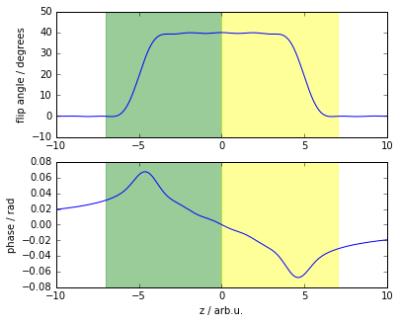
The fingerprint sequence used in this study is based on a spoiled gradient-echo sequence [2]. It consists of a train of 200 flip angles as shown in Fig. 1, preceded by an inversion pulse. The repetition times (TR) are constant at 20ms to minimize B0 artifacts, leading to a total time of 4 seconds for the 200 steps. For the present demonstration, k-space was fully sampled, but any kind of undersampling should also be possible.The measurements presented here have been performed on a Philips Achieva 3T system using an 8-channel head coil and four known gel samples (Diagnostic Sonar, Eurospin II). Six image slices were acquired with a slice thickness of 5mm and an in-plane resolution of 2.5x2.5mm². For each sample, three MRF signals were calculated using the Extended Phase Graph formalism [3], one averaged over the whole excitation slice profile for conventional mapping, and one for each of the two spatially distinct regions of the slice profile shown in Fig. 2. Matching of the spatially resolved MRF signals was performed in the following way: For each combination of substances $$$a$$$ and $$$b$$$, ratios $$$\varepsilon$$$, and relative phase factors $$$\varphi$$$, the expected signal can be expressed as

$$ S(a,b,\varepsilon,\varphi)=\varepsilon D_a^{(1)} + (1-\varepsilon)e^{i\varphi} D_b^{(2)}, $$

where $$$D_k^{(i)}$$$ is the dictionary entry for substance $$$k$$$ and sub-slice region $$$i$$$. The best match for a measured signal s is then determined by choosing the set of parameters that minimizes the inner product of the normalized signal vectors,

$$ (a^{opt}, b^{opt}, \varepsilon^{opt}, \varphi^{opt}) = \underset{(a,b,\varepsilon,\varphi)}{\mathrm{argmin}}\frac{\langle S(a,b,\varepsilon,\varphi), s\rangle}{\|S(a,b,\varepsilon,\varphi)\|\,\|s\|}. $$

Results and Discussion

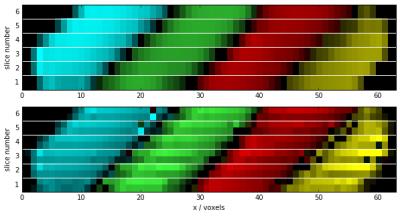
The results of a measurement of six slices through a set of four sample tubes are shown in Fig. 3. The upper image displays the sample classification using standard MRF matching (one dictionary entry per substance). The matched sample types are color-coded, while the signal magnitude is encoded in the brightness of the color. The lower image shows the same data, matched to a spatially resolved MRF dictionary as described above. Each voxel is now sub-divided into two spatially distinct parts, which are correctly classified, effectively doubling the spatial resolution. Determination of exact abundance of the sub-voxel constituents is affected by B1 inhomogeneity, so that the technique is most useful for slice thicknesses of only few millimeters.

Conclusions

Magnetic Resonance Fingerprinting can be used to retrospectively increase spatial resolution in slice-encoding direction by determining fingerprints of spatially distinct components within a voxel, making use of the non-uniform nature of the excitation slice profile. Since this technique works particularly well for a limited set of possible components, it may be used to analyze tissue boundaries of a well-defined region of interest.

Acknowledgements

No acknowledgement found.

References

[1] Ma D, Gulani, V, Seiberlich, N, et al. Magnetic resonance fingerprinting. Nature, 2013;495:187-193

[2] Jiang Y, Ma D, Seiberlich N, Gulani V, Griswold M. MR Fingerprinting using Fast Imaging with Steady State Precession (FISP) with spiral readout. Magn Reson Med 2015;74:1621-1632.

[3] Scheffler K. A pictorial description of steady-states in rapid magnetic resonance imaging. Concepts Magn Reson 1999;11:291-304.

Figures

Figure 1: Flip angle sequence used in the experiments (initial inversion pulse not shown).

Figure 2: Excitation slice profile: The colored regions indicate the two spatial regions for which separate fingerprint signals are computed. Note that the phase distribution is anti-symmetric, so that the fingerprints differ.

Figure 3: MRF classification of four substances, six slices acquired. The four sample tubes are angulated with respect to the slice-encoding direction to visualize the spatial resolution. Upper image: Conventional MRF mapping of the four substances. Lower image: Double spatial resolution due to intra-slice spatial component analysis. The white lines indicate the original slice boundaries.

Proc. Intl. Soc. Mag. Reson. Med. 25 (2017)

0131