0130
Magnetic Resonance Fingerprint Compression with Multiple Channel Transmission1Radiology, Center for Advanced Imaging Innovation and Research (CAI2R) and Bernard and Irene Schwartz Center for Biomedical Imaging, New York University School of Medicine, New York, NY, United States, 2Sackler Institute of Graduate Biomedical Sciences, New York University School of Medicine, New York, NY, United States
Synopsis
Singular value decomposition (SVD) and view-sharing compression can decrease the size of the dictionary without compromising accuracy in magnetic resonance fingerprinting (MRF). While the latter accounts for the B1+ of multiple transmit channels in the dictionary, the SVD compression scheme was designed for single-channel transmission. In this work we extended SVD-based fingerprint compression to the case of two or more independent RF sources and evaluated its performance in simulation. We showed that accurate parametric maps can be achieved using only six SVD components, both in fully-sampled and highly under-sampled MRF experiments. Future work will include optimization of k-space under-sampling.
Purpose
Given the large range of tissue and environmental parameters that one might expect to see in vivo, simulating a comprehensive dictionary of signal evolutions could result in a very large, computationally intractable database, which could hamper the magnetic resonance fingerprinting (MRF)1 reconstruction process. Two approaches have been proposed to decrease the size of the dictionary without compromising accuracy: a singular value decomposition (SVD) compression scheme that allows to shorten the fingerprints2, and a method, based on the concept of k-space view sharing3, in which an equal number of consecutive data points are added together to create a compressed fingerprint4. While the latter was developed for “Plug-and-Play MR Fingerprinting” (PnP-MRF), which accounts for the B1+ of multiple transmit channels in the dictionary4, the SVD compression scheme1 was designed for single-channel transmission. The aim of this work was to extend SVD-based fingerprint compression to the case of two or more independent RF sources and evaluate its performance.MATERIALS AND METHODS
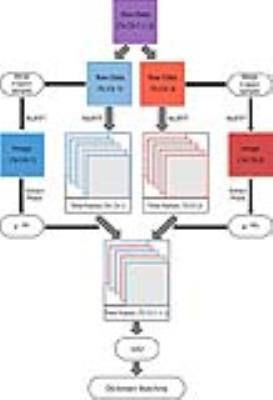
Full wave electrodynamic simulations were performed in CST Microwave Studio (Darmstadt, Germany) to obtain the B1+ distributions corresponding to the two linear modes of a circularly polarized body coil at 3T. The coil had 16 rungs, azimuthally distributed on a 60cm diameter cylinder (~2cm from the gradient shield), loaded with the Duke5 human body model (2×2×2mm3), for which a titanium implant was inserted in the right femur. Each of the tissues in the body model were assigned literature T1, T2 and PD values6,7. The two simulated B1+ profiles were employed to perform synthetic MR experiments for an axial slice through the lower extremities, using the extended phase graph formalism8 to model the PnP-MRF sequence4. The PnP-MRF sequence consists of four segments (120 time frames each), which collectively form one MR fingerprint that simultaneously identifies B1+ distribution and tissue properties. Each time point in the fingerprint was sampled with 251 (fully-sampled) and 8 (under-sampled) evenly distributed radial spokes. Individual time frames were reconstructed using a non-uniform fast Fourier transform (NUFFT)9. A fingerprint was extracted for each voxel as the signal evolution along the series of time frames and matched to values in a dictionary computed using in-house software10. Both the fingerprints simulated in the dictionary and the synthetically generated ones were compressed using the view-sharing4 and SVD approaches2. The latter cannot be applied directly with multiple transmit channels, because it would mix the signals from the various RF sources, entangling the relative transmit phases into the compressed fingerprint and causing severe artifacts in the compressed time frames. To make SVD compression suitable for multiple channel transmission we are proposing the method described in Fig.1. Following this approach, we repeated the synthetic MRF experiments for different levels of SVD compression and compared them against the view-sharing method using the same number of compressed time points.RESULTS AND DISCUSSION
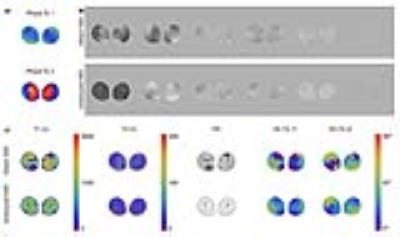
Fig.2 shows that applying SVD directly to a raw dataset that combines k-space samples associated with two RF sources resulted in large artifacts in both the compressed time frames and the reconstructed parameter maps. Artifacts were more pronounced in regions corresponding to large transceiver phase variations (Fig.2a). On the other hand, rewinding the transceiver phases before SVD compression, as outlined in Fig.1, yielded artifact-free singular images and parameter maps. Fig.3a shows that parameter values were accurate when using as few as six SVD-compressed time frames, but results would rapidly deteriorate for higher compression levels. For the same dataset, the view-sharing method performed similarly in the fully-sampled case, but required 16 compressed frames to achieve less than 10% error in the under-sampled case (Fig.3b). Note that this would not necessarily be the case for other anatomies. In fact, SVD compression is sensitive to the under-sampling strategy, since certain T1 and T2 combinations are more clearly represented in later SVD components, which can be easily corrupted by a poor choice in k-space sampling. The view sharing method does not suffer from this problem because the spokes can always be optimally reordered before compression.CONCLUSION
We presented a method to enable SVD-based MRF compression with multiple transmit channels and evaluated its performance for a dual-channel case. MRF compression is advantageous for iterative MRF reconstruction techniques11,12, since k-space is densely sampled for each compressed time point. At the same time, k-space could be highly under-sampled for the uncompressed time points, enabling both rapid acquisitions, e.g., for breath-hold clinical applications, and longer fingerprints to probe a wider range of parameter values. Future work will include investigating optimal under-sampling strategies for SVD compression and in vivo validation.Acknowledgements
This work was supported in part by NIH R21 EB020096 and NIH R01 AR070297 and was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R, www.cai2r.net), a NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).References
1. D. Ma, V. Gulani, N. Seiberlich, K. Liu, J. L. Sunshine, J. L. Duerk, and M. A. Griswold, “Magnetic resonance fingerprinting,” Nature, vol. 495, no. 7440, pp. 187–192, 2013.
2. D. F. McGivney, E. Pierre, D. Ma, Y. Jiang, H. Saybasili, V. Gulani, and M. A. Griswold, “SVD Compression for Magnetic Resonance Fingerprinting in the Time Domain,” IEEE Trans. Med. Imaging, vol. 33, no. 12, pp. 2311–2322, Dec. 2014.
3. H. K. Song and L. Dougherty, “k-Space Weighted Image Contrast (KWIC) for Contrast Manipulation in Projection Reconstruction MRI,” Magn. Reson. Med., vol. 44, no. 6, pp. 825–832, Nov. 2000.
4. Cloos, F Knoll, T Zhao, KT Block, M Bruno, GC Wiggins, DK Sodickson, “Multiparametric imaging with heterogeneous radiofrequency fields.” Nat. Commun. 2016 Aug 16;7:12445.
5. MC Gosselin, E Neufeld, H Moser, E Huber, S Farcito, L Gerber, M Jedensjö, I Hilber, F Di Gennaro, B Lloyd, E Cherubini, D Szczerba, W Kainz, N Kuster, Development of a new generation of high-resolution anatomical models for medical device evaluation: the Virtual Population 3.0, Physics in Medicine and Biology, 59(18):5287-5303, 2014.
6. CMJ Bazelaire, GD Duhamel, NM Rofsky and DC Alsop, “MR Imaging Relaxation Times of Abdominal and Pelvic Tissues Measured in Vivo at 3.0 T: Preliminary Results.” Radiology 230, 652–659 (2005).
7. FG Shellock, “Biomedical implants and devices: Assessment of magnetic field interactions with a 3.0-Tesla MR system.” J. Magn. Reson. Im. 16, 721–732 (2002). ?
8. M Weigel, “Extended phase graphs: Dephasing, RF pulses, and echoes - pure and simple.” J. Magn. ?Reson. Im. 41, 266–295 (2014).
9. JA Fessler and BP Sutton, "Nonuniform fast Fourier transforms using min-max interpolation," IEEE Transactions on Signal Processing, vol. 51, no. 2, pp. 560-574, Feb 2003.
10. https://bitbucket.org/macloos/pnp-mrf/wiki/Home/
11. B Zhao, “Model-based iterative reconstruction for magnetic resonance fingerprinting,” Proceedings - International Conference on Image Processing, ICIP, 2015, vol. 2015, pp. 3392–3396.
12. J Assländer, MA Cloos, F Knoll, DK Sodickson, J Hennig, and R Lattanzi, “Low Rank Alternating Direction Method of Multipliers Reconstruction for MR Fingerprinting,” preprint, p. arXiv:1608.06974, 2016.
Figures