0086
Uniform Spatiotemporal Excitation Despite Extreme B0 Inhomogeneity Using Dynamically-Driven Multi-Coil Arrays1Center for Magnetic Resonance Research, University of Minnesota, Minnesota, MN, United States, 2Departments of Biomedical Engineering and Radiology, Columbia University in the City of New York, NY, United States, 3Center for Magnetic Resonance Research, University of Minnesota, MN, United States, 4Center for Magnetic Resonance Research, University of Minnesota, Minnesota, United States, 5Department of Radiology and Biomedical Imaging, Yale University School of Medicine, NY, United States
Synopsis
Developments of new imaging strategies that tolerate extreme B0 inhomogeneity can reduce size and cost of MRI magnets; but with conventional MRI methods, a highly uniform B0 is still required to obtain high quality images. Previously we demonstrated spatiotemporal excitation of spins in the presence of large B0 inhomogeneity when driving a multi-coil array with the dynamic multi-coil technique known as DYNAMITE. In that work, tolerance to B0 inhomogeneity began to degrade when the frequency variation exceeded +/-40 kHz, which is insufficient for imaging with a small magnet. Here we present a technique to substantially extend the range of B0 inhomogeneity tolerance of this approach when using RF pulses based on the principle of offset-independent adiabaticity (OIA).
Introduction
Conventional approaches to MR imaging require a relatively uniform static magnetic field (B0), producing frequency variation on the order of only 1 – 2 ppm (e.g., ~100 – 300 Hz). As such, MRI magnets must be physically large relative to the object to be imaged, which increases the expense of magnets and their siting. The MRI method called STEREO (for STEering REsonance over the Object) generates images by moving a locally shimmed region along a curved trajectory in space such that the excitation of spins itself is spatially selective 1,2. Previously we investigated the feasibility of creating spatiotemporal excitation of spins with STEREO by dynamically driving the coil currents in a multi-coil array with the dynamic multi-coil technique (DYNAMITE) while applying constant RF irradiation 3. In that work, it was observed that the uniform spatiotemporal excitation of spins was not taking place in the presence of constant RF pulse when B0 inhomogeneity exceeded +/-40 kHz 4. Therefore, in the present study, we investigate the feasibility of using DYNAMITE while applying a modulated offset-independent adiabatic (OIA) RF pulse to create uniform spatiotemporal excitation with STEREO, despite extreme B0-induced frequency variation (e.g., +/-100 kHz).Materials and Methods
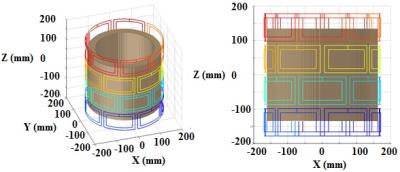
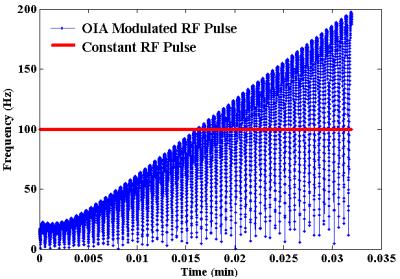
After selection of center positions of the current carrying coils on the cylindrical surface (Fig 1), the z-component of the magnetic field generated by the coils per unit current was then derived analytically by use of the Biot-Savart law 4. Equivalent values in hertz were derived using the Larmor equation for protons (1H). For this simulation study, an uncorrected static B0 having amplitude proportional to (x2 – y2) was generated within a 256x256x256 mm3 FOV using a 64x64x64 matrix. DYNAMITE was then used to create a spatiotemporal variation (a parabolic-shaped field distribution with amplitude = 500 Hz/cm2) that traversed on a 2D spiral trajectory of 16 turns and total duration TP of 32 ms. To evaluate the ability to excite spins in an inhomogeneous B0, Bloch simulations were performed with 0, +/-20, +/- 40 , and +/- 100 kHz, while applying either a constant RF pulse of amplitude ω1 (=100 Hz) or an OIA-modulated RF pulse, with amplitude function ωMOD given by
$$\omega_{MOD}^2=K.\frac{d\omega}{ds}$$(1)
Here dω/ds is the spatial variation of the frequency along the spiral trajectory, dω is the infinitesimal resonance frequency change evaluated at the vertex of the parabolic function, and ds is the infinitesimal line element (Eq.2.) along the direction of spiral trajectory at any given moment. In Cartesian coordinates, the small infinitesimal displacement ds vector can be decomposed into
$$\overrightarrow{ds}=dx\widehat{i}+dy\widehat{j}$$(2)
where i and j are unit vectors along the x and y directions respectively. For a fair comparison of the two spatiotemporal excitation schemes, the constant Κ (Eq.1.) was set to maintain same total RF energy for the two approaches:
$$K=\sqrt{\int_{0}^{T_p} \frac{dt.\omega_1^2}{dt(\frac{d\omega}{ds})^2}}$$(3)
The constant and OIA-modulated RF pulses are shown in Fig.2. The maximum transverse magnetization (Mxy) generated by these pulses in the presence of increasing B0 inhomogeneity was evaluated in Bloch simulations. Potential relaxation effects were not considered in the simulations.
Results
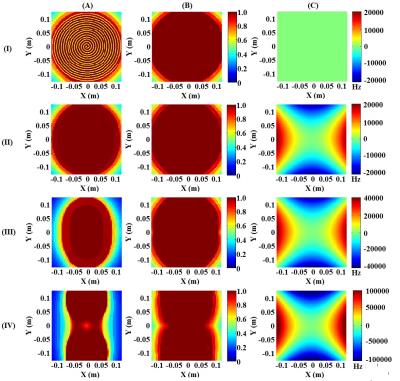
Fig 3 shows the MXY produced by a constant RF field of 100 Hz (A) and the equivalent OIA-modulated RF (B), when B0 (C) produced frequency variation equal to zero (I), +/- 20 kHz (II), +/-40 kHz (III), and +/-100 kHz (IV). As can be seen, the OIA-modulated RF pulse provided the highest level of compensation for B0 inhomogeneity.
Discussion
In this work, simulations have provided proof-of-concept of a way to excite spins despite extreme B0 inhomogeneity using dynamically driven coil currents in a multi-coil array (DYNAMITE) while applying an OIA-modulated RF pulse. The next step will involve experimental validation of this spatiotemporal excitation as a means to accomplish MR imaging in extreme field inhomogeneity.
Acknowledgements
NIH grant R24 MH105998.References
1.Snyder L,Curtis A, et al. MRI by Steering Resonance Through Space. Magn. Reson. Med. 2014;72:49-58.
2.Jang A, Kobayashi N, et al. 2D Pulses Using Spatially Dependent Frequency Sweeping. Magn. Reson. Med. 2016;76:1364-1374.
3.Juchem C, Nixon T, et al. Magnetic Field Modeling with a Set of Individual Localized Coils. J Magn Reson. 2010;204:281–289.
4.Jayatilake M, Juchem C, et al. STEREO-MC for Connected Spatiotemporal Excitation. Proc. Intl. Soc. Mag. Reson. Med. 2016; 24.
Figures