0084
Accelerated Imaging of Metallic Implants Using a Double-Peak-Model Constraint1Radiology, Stanford University, Stanford, CA, United States, 2Electrical Engineering, Stanford University, Stanford, CA, United States
Synopsis
Multi-Spectral Imaging (MSI) enables MRI near metallic implants, but suffers from prolonged scan times. Model-based reconstruction accelerates MSI by enforcing a signal model along the spectral dimension to reduce the number of unknowns in image reconstruction. The previous signal model assumes that spins in one voxel have the same off-resonance frequency, which tends to fail where the off-resonance field changes rapidly. Here we propose a more flexible MSI signal model that allows multiple frequencies within a voxel, and demonstrate improvements with both simulated and in-vivo data. 3x net additional acceleration above partial-Fourier and parallel-imaging alone (20x in total) was achieved.
Purpose
Imaging near metallic implants is challenging due to large magnetic field perturbations induced by metal. Multi-Spectral Imaging (MSI) techniques, such as SEMAC1 and MAVRIC-SL2, resolve the field perturbations by acquiring separate 3D spatial encodings for multiple spectral bins, at the cost of long scan time. Various methods have been investigated to accelerate MSI3-9, among which model-based reconstruction9 has the advantage of fully exploiting the correlation between spectral bins by enforcing a signal model to describe the signal profile across bins. This reduces the number of unknowns in the reconstruction from 20+ spectral bins to 2 parameters.
The previous MSI signal model assumes that spins in one voxel have the same off-resonance frequency. This assumption tends to fail near high-susceptibility implants where the off-resonance field changes rapidly, resulting in artifacts in the reconstructed images. Here we propose a flexible MSI signal model that allows multiple frequencies within a voxel, and demonstrate improvements using both simulated and in-vivo data.
Theory
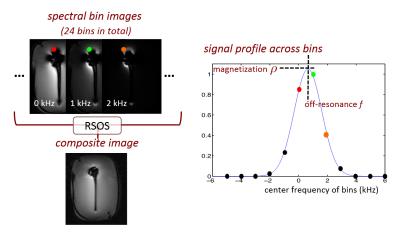
As shown in Fig.1, over 20 spectral bin images are acquired at different center frequencies in MSI. Based on the Gaussian RF pulses used in MAVRIC-SL, the original signal model uses two parameters, magnetization $$$\rho(r)$$$ and off-resonance frequency $$$f(r)$$$, to represent the bin images as$$m_b^{\mathrm{original}}(r)=\rho(r)\cdot\exp\{-(f(r)-f_b)^2/2\sigma^2\}\hspace{10mm}(\mathrm{Eq.1})$$
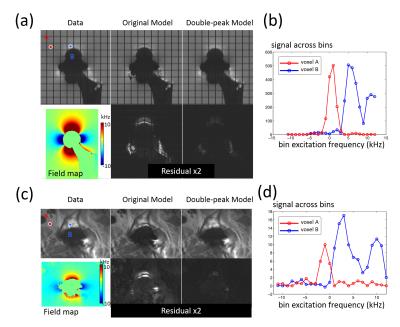
where $$$b$$$ is the bin index, $$$f_b$$$ denotes the center frequency of bin $$$b$$$ and $$$\sigma$$$ denotes the width of RF frequency profile. $$$f_b$$$ and $$$\sigma$$$ are known sequence parameters. All bins are demodulated at a single frequency, so that off-resonance-induced pixel displacements match across bins. However, with this demodulation scheme, spins with varying off-resonance frequencies can be shifted to the same location, and the signal profile across bins will have a broader peak or even two peaks (Fig.2). The second peak in the signal model only appears in a small region near metal where the off-resonance frequency varies rapidly in the readout direction. This effect is considered in the new double-peak model given by$$m_b^{\mathrm{double-peak}}(r)=\Sigma_{p=1,2}{\rho_p(r)\cdot\exp\{-(f_p(r)-f_b)^2/2s_p(r)\}}\hspace{10mm}(\mathrm{Eq.2})$$
where $$$s_p(r)$$$ denotes the width of the signal profile, two sets of parameter maps indexed by $$$p$$$ are used to represent the double-peak situation. The second set of parameters is only included in a small region near metal determined during initialization.
The reconstruction problem is$$ \mathrm{minimize}_{\rho_p(r),f_p(r),s_p(r)}{\Sigma_b\|M_b\cdot{}F\{m_b^{\mathrm{double-peak}}(r)\}-\hat{y}_b\|_2^2+\lambda\Sigma_{p=1,2}{\mathrm{TV}(\rho_p(r))}}\hspace{10mm}(\mathrm{Eq.3})$$
where $$$M_b$$$ represents the under-sampling mask, $$$F$$$ represents the Fourier transform, and $$$\hat{y}_b$$$ represents the acquired k-space data. A limited-memory BFGS algorithm10 is used to solve (3). The spectral bin images are synthesized from the resulting parameter maps, demodulated at the center frequency of each bin, and combined by root-sum-of-squares to form the composite image.
Method
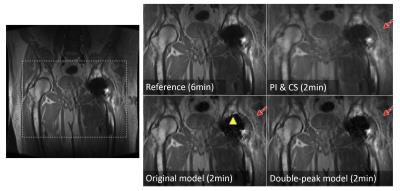
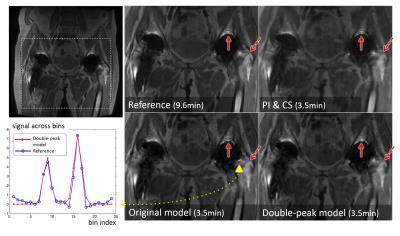
To validate the accuracy of the double-peak model, the fitting residuals of the model were computed on simulated data of a digital phantom with a hip implant, and in-vivo data of a volunteer with a total hip replacement. The reconstruction was tested in MAVRIC-SL scans of two volunteers with hip implants. All scans were performed on GE 3T MRI systems with 24 spectral bins spanning ±12kHz, ±125kHz readout bandwidth, 2x2 uniform under-sampling and half-Fourier acquisition. Other scan parameters include: (subject 1) 8-channel cardiac array, matrix size=384x256x24, voxel size=1.1x1.7x4.0mm3, scan time=6.0min; (subject 2)32-channel torso array, matrix size=384x256x44, voxel size=1.0x1.6x4.0mm3, scan time=9.6min. The outer k-space was further under-sampled by 4 using Poison-disc sampling. The results of the new model were compared with the original model and bin-by-bin parallel imaging and compressed sensing(PI&CS).Results & Discussion
As both simulated and in-vivo results in Fig.2 show, in most places the original model described the signal profile across bins well, while the double-peak model was necessary in regions of rapidly varying off-resonance, like voxel B. The double-peak model effectively reduced the fitting residual in these regions. The remaining residual for the double-peak model came from the asymmetric peaks in signal profiles, such as voxel B in Fig. 2d.
The comparison of reconstructed images in Figs.3&4 shows that incorporating the double-peak model suppressed the artifacts (signal oscillations and signal loss) near the surface of the implants compared to results of the original model (arrowheads). The locations of these artifacts were consistent with the areas where the original model had large residuals in Fig.2a&c. Both model-based reconstruction results showed sharper details compared with bin-by-bin PI&CS(dashed arrows).
Conclusion
A double-peak model of MSI signals in the spectral dimension was demonstrated to be more accurate in regions with rapidly varying off-resonance than the original model, and reduced the related artifacts in vicinity of metal. As demonstrated with the in-vivo scans, the model-based reconstruction maintains high image quality at 3x net additional acceleration above partial Fourier and parallel imaging alone (20x acceleration in total).Acknowledgements
NIH R01 EB017739, R21 EB019723, P41 EB015891, research support from GE Healthcare.References
[1] Lu et. al, MRM 62:66-76, 2009; [2] Koch et. al, MRM 65:71-82, 2011; [3] Hargreaves et. al, JMRI , 31: 987–996. 2010; [4] Worters et. al, JMRI 37:243–248, 2013; [5] Koch et. al, ISMRM 2011, p3172; [6] Sveinsson et. al, MRM 73: 662-668, 2015; [7] Smith et. al, MRM 72:1658–1667; [8] Otazo et, al, MRM Early View, 2016; [9] Shi et. al, ISMRM 2016, p 47; [10] M. Schmidt: http://www.cs.ubc.ca/~schmidtm/Software/minFunc.html, 2005.Figures